解算微分代数方程 (DAE)

什么是微分代数方程？

微分代数方程是一类微分方程，其中一个或多个因变量导数未出现在方程中。方程中出现的未包含其导数的变量称为代数变量，代数变量的存在意味着您不能将这些方程记为显式形式 $y' = f (t, y)$ 。相反，您可以解算下列形式的 DAE：

ode15s 和 ode23t 求解器可以使用奇异质量矩阵 $M (t, y) y' = f (t, y)$ 来解算微分指数为 1 的线性隐式问题，包括以下形式的半显式 DAE
$\begin{matrix} y' = f (t, y, z) \\ 0 = g (t, y, z) . \end{matrix}$
在此形式中，由于主对角线存在一个或多个零值，因此代数变量的存在会产生奇异质量矩阵。
$M y' = (\begin{matrix} y'_{1} & 0 & \dots & 0 \\ 0 & y'_{2} & 0 & ⋮ \\ ⋮ & 0 & ⋱ & 0 \\ 0 & \dots & 0 & 0 \end{matrix}) .$
默认情况下，求解器会自动检验质量矩阵的奇异性，以检测 DAE 方程组。如果您提前知道奇异性，则可将 odeset 的 MassSingular 选项设为 'yes'。对于 DAE，您还可以使用 odeset 的 InitialSlope 属性为求解器提供 $y'_{0}$ 的初始条件估计值。除此之外，还可在调用求解器时指定 $y_{0}$ 的常用初始条件。
ode15i 求解器可解算更通用的完全隐式形式的 DAE
$f (t, y, y') = 0 .$
在完全隐式形式下，代数变量的存在会产生奇异雅可比矩阵。这是因为，由于至少有一个变量的导数没有出现在方程中，因此矩阵中的对应列必定全部为零值。
$J = \partial f / \partial y' = (\begin{matrix} \frac{\partial f_{1}}{\partial y'_{1}} & \dots & \frac{\partial f_{1}}{\partial y'_{n}} \\ ⋮ & ⋱ & ⋮ \\ \frac{\partial f_{m}}{\partial y'_{1}} & \dots & \frac{\partial f_{m}}{\partial y'_{n}} \end{matrix})$
ode15i 求解器要求您同时为 $y'_{0}$ 和 $y_{0}$ 指定初始条件。此外，与其他 ODE 求解器不同，ode15i 要求为方程编码的函数能够接受额外输入：odefun(t,y,yp)。

DAE 会产生各种方程组，因为物理守恒定律通常具有类似 $x + y + z = 0$ 这样的形式。如果已在方程中显式定义 x、x'、y 和 y'，则此守恒方程无需 z' 表达式便足以解算 z。

一致的初始条件

在解算 DAE 时，可以同时为 $y'_{0}$ 和 $y_{0}$ 指定初始条件。ode15i 求解器要求同时将这两个初始条件指定为输入参数。对于 ode15s 和 ode23t 求解器， $y'_{0}$ 的初始条件是可选的（但可使用 odeset 的 InitialSlope 选项指定）。这两种情况下，您所指定的初始条件可能与正在尝试解算的方程不相符。彼此冲突的初始条件称为不一致。初始条件的处理因求解器而异：

ode15s 和 ode23t - 如果您没有为 $y'_{0}$ 指定初始值，则求解器会自动基于您为 $y_{0}$ 提供的初始条件计算一致的初始条件。如果您为 $y'_{0}$ 指定了不一致的初始条件，则求解器会将这些值作为估计值进行处理，尝试计算接近估计值的一致值，并继续解算该问题。
ode15i - 您为求解器提供的初始条件必须一致，并且 ode15i 不会检查所提供的值的一致性。辅助函数 decic 可计算满足这一要求的一致初始条件。

微分指数

DAE 的特征是其作为奇异性度量的微分指数。通过对方程进行微分，可以消除代数变量，并且如果执行此操作的次数足够多，这些方程将呈现为显式 ODE 方程组。DAE 方程组的微分指数是为了将方程组表示为等效的显式 ODE 方程组必须执行的求导次数。因此，ODE 的微分指数为 0。

微分指数为 1 的 DAE 示例如下

$y (t) = k (t) .$

对于此方程，只需执行一次求导便可获得显式 ODE 形式

$y' = k' (t) .$

微分指数为 2 的 DAE 示例如下

$\begin{array}{l} y'_{1} = y_{2} \\ 0 = k (t) - y_{1} . \end{array}$

这些方程要求进行两次求导才能重写为显式 ODE 形式

$\begin{array}{l} y'_{1} = k' (t) \\ y'_{2} = k'' (t) . \end{array}$

ode15s 和 ode23t 求解器仅可解算微分指数为 1 的 DAE。如果您的方程微分指数为 2 或更高，则需要将方程重写为微分指数为 1 的等效 DAE 方程组。您可随时对 DAE 方程组求导并将其重写为微分指数为 1 的等效 DAE 方程组。请注意，如果您将代数方程替换为其导数，则可能已删除某些约束。如果这些方程不再包含原始约束，则数值解可能发生漂移。

如果您有 Symbolic Math Toolbox™，则请参阅Solve Differential Algebraic Equations (DAEs) (Symbolic Math Toolbox) 以获取详细信息。

施加非负性

odeset 的大多数选项与 DAE 求解器 ode15s、ode23t 和 ode15i 一起使用时能按预期工作。然而，一个明显的例外是使用 NonNegative 选项。NonNegative 选项不支持应用于具有质量矩阵的问题的隐式求解器（ode15s、ode23t、ode23tb）。因此，您不能使用此选项对 DAE 问题施加非负性约束，DAE 问题一定有奇异质量矩阵。有关详细信息，请参阅[1]。

将 Robertson 问题作为半显式微分代数方程 (DAE) 求解

打开脚本

此示例将 ODE 方程组重新表示为微分代数方程组 (DAE)。hb1ode.m 中的 Robertson 问题是刚性 ODE 解算程序的经典测试问题。方程组为：

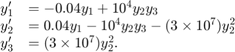
$\begin{array}{cl} y'_1 &= -0.04y_1 + 10^4 y_2y_3\\ y'_2 &= 0.04y_1 -
10^4 y_2y_3- (3 \times 10^7)y_2^2\\ y'_3 &= (3 \times
10^7)y_2^2.\end{array}$

hb1ode 将此 ODE 方程组解算为稳定状态，初始条件为、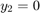和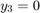。但这些方程也满足线性守恒定律，

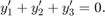
在解和初始条件方面，守恒定律为

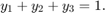
通过使用守恒定律确定的状态，该方程组可以重写为 DAE 方程组。这会将问题重新表示为 DAE 方程组

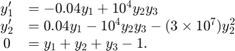
$\begin{array}{cl} y'_1 &= -0.04y_1 + 10^4 y_2y_3\\ y'_2 &= 0.04y_1 -
10^4 y_2y_3-(3 \times 10^7)y_2^2\\ 0 &= y_1 + y_2 + y_3 - 1.\end{array}$

此方程组的微分指数为 1，因为只需的一个导数就能使其成为 ODE 方程组。因此，在解算该方程组之前，不需要进行更多变换。

函数 robertsdae 为此 DAE 方程组编码。将 robertsdae.m 保存在您的当前文件夹中，以运行该示例。

function out = robertsdae(t,y)
out = [-0.04*y(1) + 1e4*y(2).*y(3)
   0.04*y(1) - 1e4*y(2).*y(3) - 3e7*y(2).^2
   y(1) + y(2) + y(3) - 1 ];

hb1dae.m 中提供了用这种方法表示 Robertson 问题的完整示例代码。

使用 ode15s 解算 DAE 方程组。根据守恒定律，显然需要一致的 y0 初始条件。使用 odeset 设置选项：

使用常量质量矩阵表示方程组的左侧。

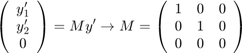
$\left( \begin{array}{c} y'_1\\ y'_2\\ 0 \end{array} \right) = M y'
\rightarrow M = \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 &
0 \end{array} \right)$

将相对误差容限设为 1e-4。
使用 1e-10 的绝对误差作为第二个解分量，因为标度范围与其他分量相差很大。
将 'MassSingular' 选项保留其默认值 'maybe'，以测试 DAE 的自动检测。

y0 = [1; 0; 0];
tspan = [0 4*logspace(-6,6)];
M = [1 0 0; 0 1 0; 0 0 0];
options = odeset('Mass',M,'RelTol',1e-4,'AbsTol',[1e-6 1e-10 1e-6]);
[t,y] = ode15s(@robertsdae,tspan,y0,options);

对解绘图。

y(:,2) = 1e4*y(:,2);
semilogx(t,y);
ylabel('1e4 * y(:,2)');
title('Robertson DAE problem with a Conservation Law, solved by ODE15S');

参考

[1] Shampine, L.F., S. Thompson, J.A. Kierzenka, and G.D. Byrne. “Non-Negative Solutions of ODEs.” Applied Mathematics and Computation 170, no. 1 (November 2005): 556–569. https://doi.org/10.1016/j.amc.2004.12.011.