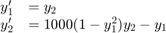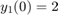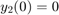ode23tb
求解刚性微分方程 - 梯形法则 + 后向差分公式
语法
说明
sol = ode23tb(___)deval 结合使用来计算区间 [t0 tf] 中任意点位置的解。您可以使用上述语法中的任何输入参量组合。
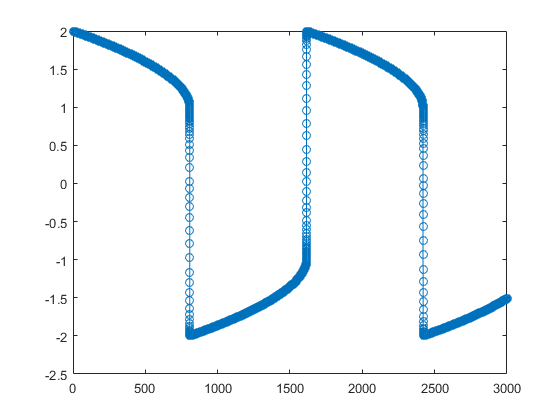
示例
输入参数
输出参量
算法
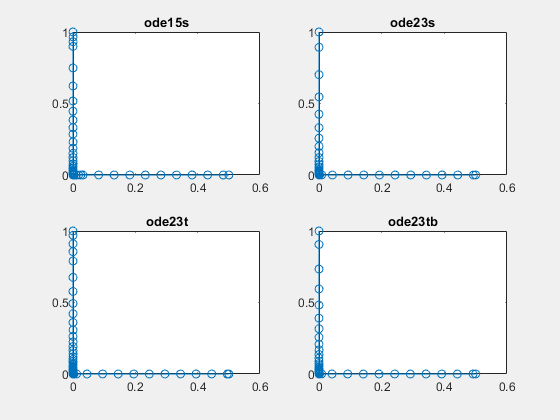
ode23tb 是 TR-BDF2 的实现,这是一个隐式龙格-库塔公式,该公式第一阶段计算采用梯形法则步,第二阶段计算采用二阶后向差分公式。从构造上而言,两级计算使用相同的迭代矩阵。与 ode23s 和 ode23t 一样,此求解器在解算具有宽松容差的问题时,可能效率高于 ode15s [1], [2]。
参考
[1] Bank, R. E., W. C. Coughran, Jr., W. Fichtner, E. Grosse, D. Rose, and R. Smith, “Transient Simulation of Silicon Devices and Circuits,” IEEE Trans. CAD, 4 (1985), pp. 436–451.
[2] Shampine, L. F. and M. E. Hosea, “Analysis and Implementation of TR-BDF2,” Applied Numerical Mathematics 20, 1996.
版本历史记录
在 R2006a 之前推出