ribbon
条带图

说明
ribbon(___, 使用一个或多个名称-值参量设置条带图的属性。例如,您可以指定条带的颜色和透明度。有关属性列表,请参阅 Surface 属性。 (自 R2024b 起)Name=Value)
s = ribbon(___) 返回一个由 Surface 对象组成的向量,每个对象对应一个条带。创建绘图后,使用 s 修改该绘图的属性。有关属性列表,请参阅 Surface 属性。
示例
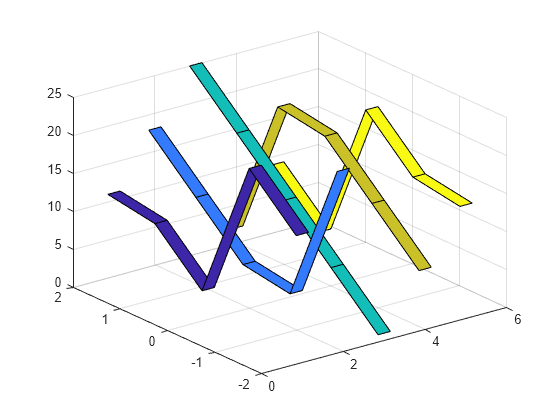
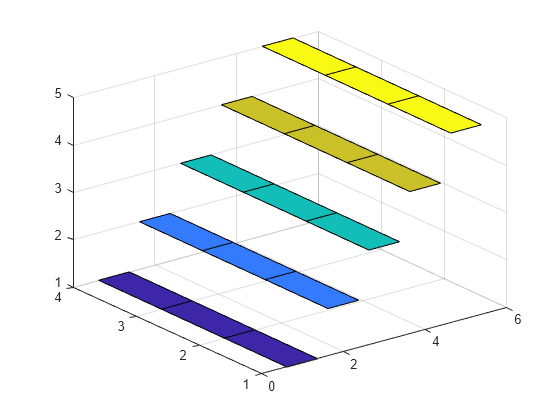
创建一个包含五个高度递增的条带的图。首先,创建一个 5×5 矩阵,其中的元素对应于条带高度。
Z = repmat(1:5,4,1)
Z = 4×5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
Z 的每列表示一个条带,在对应于列号的常量 x 坐标和对应于 Z 的行号的 y 坐标上绘制。
ribbon(Z)
使用 magic 函数创建一个 5×5 矩阵。
Z = magic(5)
Z = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
创建矩阵的条带图,并指定 y 坐标,使每个条带以 0 为中心。
Y = [-2 -1 0 1 2]; ribbon(Y,Z);
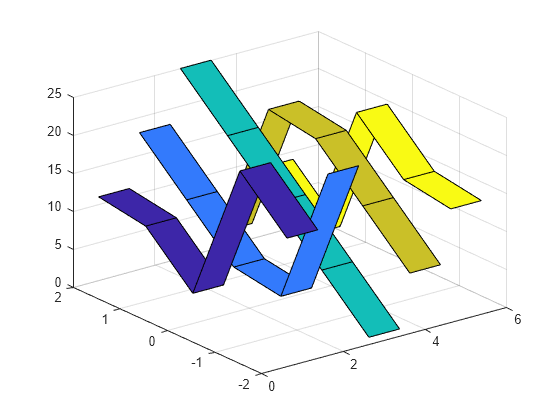
在沿 y 轴的不同位置上绘制三个条带。将条带的 y 坐标指定为矩阵 Y,其大小与条带高度矩阵 Z 相同。Y 的每列对应一个条带。
Y = [1 2 3;
2 3 4;
3 4 5;
4 5 6];
Z = Y;
ribbon(Y,Z)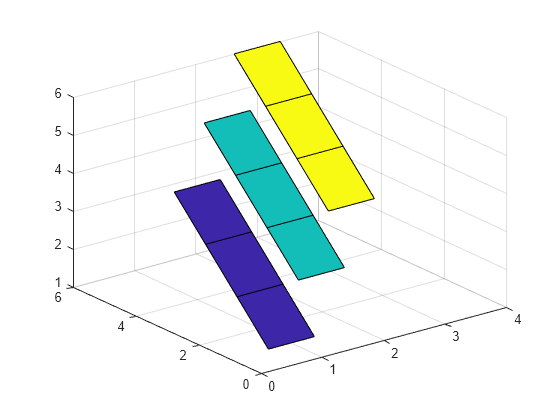
创建条带图并指定输出参量。输出是一个由五个 Surface 对象组成的向量,其中每个对象对应一个条带。
Z = magic(5); Y = [-2 -1 0 1 2]; s = ribbon(Y,Z)
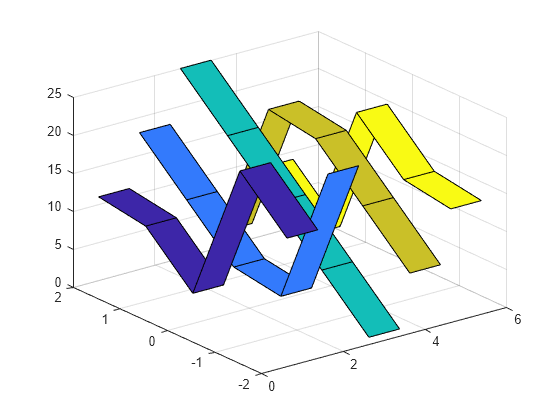
s = 5×1 Surface array: Surface Surface Surface Surface Surface
通过更改对应 Surface 对象的 EdgeColor 和 LineWidth 属性,突出显示第一个条带。
s(1).EdgeColor = "yellow";
s(1).LineWidth = 3;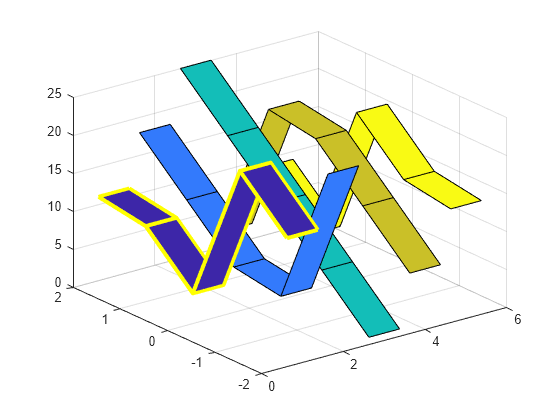
创建一个包含 30 个条带和一个颜色栏的条带图。
t = linspace(0,2*pi,30);
x = sin(t)';
y = cos(t);
ribbon(x*y)
cbar = colorbar;
cbar.Label.String= "Ribbon Number";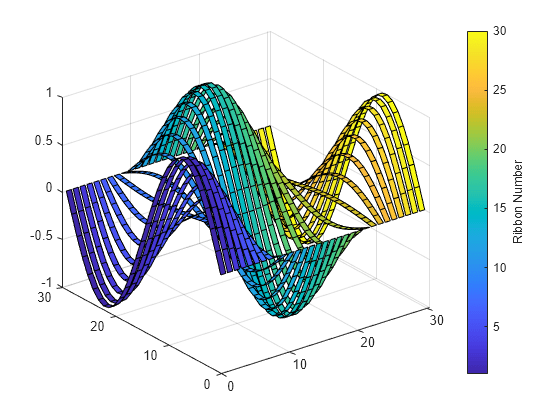
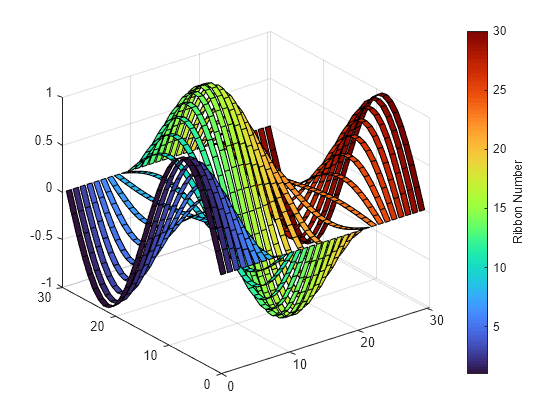
使用 colormap 函数更改条带颜色。ribbon 将条带的 x 坐标线性映射到颜色图中的颜色。
colormap(turbo)
输入参数
表示条带高度的 z 坐标,指定为数值向量或数值矩阵。
如果
Z是向量,则无论Z是行向量还是列向量,ribbon都会创建单个条带。如果
Z是矩阵,ribbon将为每列创建一个条带。各条带沿 x 轴排列,且居中置于单位间隔处,其中 x 坐标的范围是从 1 到Z中的列数。
y 坐标,指定为数值向量或数值矩阵。Z 的大小确定 Y 的可能大小:
如果
Z是向量,Y必须为与Z大小相同的向量。ribbon使用Y和Z中的数据在X = 1处绘制单个条带。如果
Z是矩阵,Y可以是长度等于Z中行数的行向量或列向量,或是与Z大小相同的矩阵。ribbon使用Y和Z中的数据为Z中的每一列绘制一个条带。如果Y是向量,则每个条带都有相同的 y 坐标。
条带宽度,指定为表示每个条带可用总空间的百分比的数值标量。
如果
width < 1,条带宽度将占据分配空间的一部分。如果
width = 1,则各条带相互接触,沿 z 轴向下查看时它们紧挨在一起。如果
width > 1,则条带相互重叠并可能相交。
例如,默认值 0.75 表示条带宽度是条带可用总空间的 75%,每侧有 12.5% 的空白空间。
目标坐标区,指定为 Axes 对象。如果未指定坐标区,则 MATLAB® 将在当前坐标区中进行绘制;或如果不存在 Axes 对象,则创建一个对象。
名称-值参数
以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组,其中 Name 是参量名称,Value 是对应的值。名称-值参量必须出现在其他参量之后,但参量对组的顺序无关紧要。
示例: ribbon([1 2 3; 1 2 3],FaceColor="red") 创建一个红色条带图。
注意
此处所列的属性只是一部分。有关完整列表,请参阅 Surface 属性。
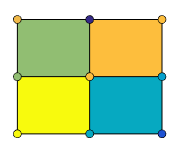
面颜色,指定为下表中的值之一。
| 值 | 描述 |
|---|---|
'flat' | 根据
|
'interp' | 根据
|
| RGB 三元组、十六进制颜色代码或颜色名称 | 对所有面使用指定的颜色。此选项不会使用
|
'texturemap' | 变换 CData 中的颜色数据,以便其符合曲面。 |
'none' | 不绘制面。 |
RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。十六进制颜色代码是字符向量或字符串标量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外,还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如,获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
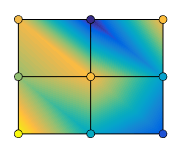
面透明度,指定为下列值之一:
范围
[0,1]中的标量 - 在所有面上使用统一的透明度。值为1时完全不透明,值为0时完全透明。介于0和1之间的值表示半透明。此选项不会使用AlphaData属性中的透明度值。'flat'- 根据AlphaData属性中的值,对每个面使用不同的透明度。第一个顶点的透明度值确定整个面的透明度。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。FaceColor属性也必须设置为'flat'。'interp'- 根据AlphaData属性中的值,对每个面使用插值透明度。通过基于各顶点处透明度数值进行插值,每个面上的透明度会渐变。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。FaceColor属性也必须设置为'interp'。'texturemap'- 变换AlphaData中的数据,以便其符合曲面。
边线颜色,指定为下面列出的值之一。默认颜色 [0 0 0] 对应于黑边。
| 值 | 描述 |
|---|---|
'none' | 不绘制边。 |
'flat' | 根据
|
'interp' | 根据
|
| RGB 三元组、十六进制颜色代码或颜色名称 | 对所有边使用指定的颜色。此选项不会使用
|
RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。十六进制颜色代码是字符向量或字符串标量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外,还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如,获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
边透明度,指定为下列值之一:
[0,1]范围内的标量 - 在所有边上都使用统一的透明度。值为1时完全不透明,值为0时完全透明。介于0和1之间的值表示半透明。此选项不会使用AlphaData属性中的透明度值。'flat'- 根据AlphaData属性中的值,对每个边使用不同透明度。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。第一个顶点上的透明度值确定整条边的透明度。EdgeColor属性也必须设置为'flat'。'interp'- 根据AlphaData属性中的值,对每个边使用插值透明度。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。通过基于各顶点处值进行插值,每条边上的透明度会渐变。EdgeColor属性也必须设置为'interp'。
扩展功能
ribbon 函数支持 GPU 数组输入,但有以下用法说明和限制:
此函数接受 GPU 数组,但不在 GPU 上运行。
有关详细信息,请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。
版本历史记录
在 R2006a 之前推出通过指定名称-值参量来控制条带图的外观和行为。以前,ribbon 不支持名称-值参量。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)