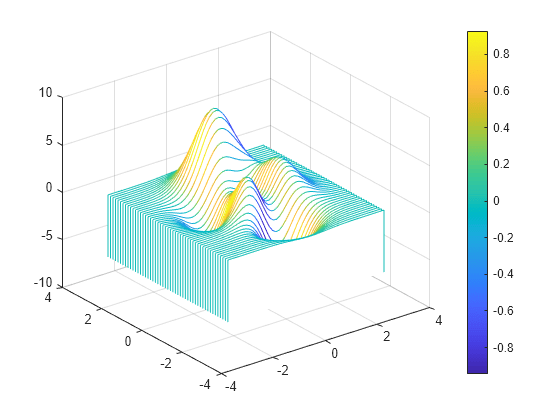
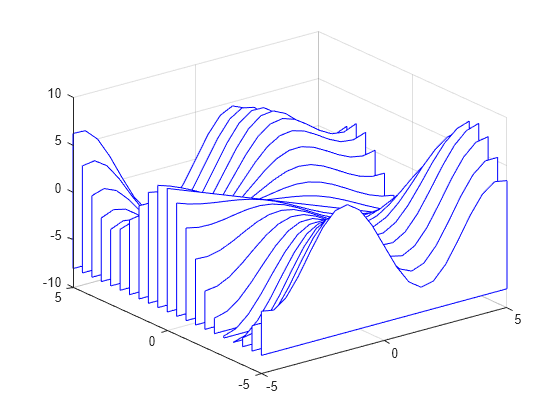
waterfall
瀑布图
语法
说明
waterfall( 创建一个瀑布图，并将 Z)Z 中元素的列索引和行索引用作 x 坐标和 y 坐标。
waterfall(___, 使用一个或多个名称-值参量设置瀑布图的属性。例如，您可以指定图边的颜色和粗细。有关属性列表，请参阅 Patch 属性。 (自 R2024b 起)Name=Value)
waterfall( 将图形绘制到 ax,___)ax 指定的坐标区中，而不是当前坐标区中。指定坐标区作为第一个输入参量。此参量可用于上述任一输入语法。
示例
创建三个相同大小的矩阵。然后将它们绘制为一个瀑布图。网格图使用 Z 确定高度和颜色。
[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); waterfall(X,Y,Z)
通过包含第四个矩阵输入 C 来指定瀑布图的颜色。瀑布图使用 Z 表示高度，C 表示颜色。向图中添加颜色栏以显示 C 中的数据值如何对应于颜色图中的颜色。
[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); C = gradient(Z); waterfall(X,Y,Z,C) colorbar
创建一个瀑布图。要允许进一步修改，请将补片对象赋给变量 p。
[X,Y] = meshgrid(-5:.5:5); Z = Y.*sin(X) - X.*cos(Y); p = waterfall(X,Y,Z)
p =
Patch with properties:
FaceColor: [1 1 1]
FaceAlpha: 1
EdgeColor: 'flat'
LineStyle: '-'
Faces: [21×26 double]
Vertices: [546×3 double]
Show all properties
在创建瀑布图之后可使用 p 访问并修改其属性。例如，通过设置 EdgeColor 属性来更改图边的颜色。
p.EdgeColor = 'b';
通过转置输入参量，沿 x 维度（而不是 y 维度）显示部分帷幕。
[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); waterfall(X',Y',Z')
输入参数
名称-值参数
以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但参量对组的顺序无关紧要。
示例: waterfall(peaks,LineStyle="--") 使用虚线创建一个瀑布图。
注意
此处所列的属性只是一部分。有关完整列表，请参阅 Patch 属性。
边颜色，指定为下表中的值之一。默认边颜色为黑色，值为 [0 0 0]。如果多个多边形共用一条边，则最先绘制的多边形将控制显示的边颜色。
| 值 | 描述 | 结果 |
|---|---|---|
RGB 三元组、十六进制颜色代码或颜色名称 | 所有边使用一种颜色。如需更多详细信息，请参阅下表。 |
|
'flat' | 每条边使用不同颜色。使用顶点颜色设置该顶点之后的边的颜色。您必须先将 |
|
'interp' | 插入的边颜色。您必须先将 |
|
'none' | 不显示边。 | 不显示边。 |
RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。
RGB 三元组是包含三个元素的行向量，其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内，例如[0.4 0.6 0.7]。十六进制颜色代码是字符向量或字符串标量，以井号 (
#) 开头，后跟三个或六个十六进制数字，范围可以是0到F。这些值不区分大小写。因此，颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外，还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如，获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
线型，指定为下表中列出的选项之一。
| 线型 | 描述 | 表示的线条 |
|---|---|---|
"-" | 实线 |
|
"--" | 虚线 |
|
":" | 点线 |
|
"-." | 点划线 |
|
"none" | 无线条 | 无线条 |
提示
要以列（而不是行）形式分析数据，请调用带转置参量的
waterfall：[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); waterfall(X',Y',Z')
要创建网格曲面对象而不是补片对象，请使用
meshz函数。要创建类似瀑布图的图，请将曲面的MeshStyle属性设置为'Row'。
算法
坐标区的
XLim、YLim和ZLim属性存储 x、y 和 z 轴的范围。这些范围基于X、Y和Z输入参量的范围。坐标区的
CLim属性确定颜色在C范围内的分布。有关详细信息，请参阅控制颜色图范围。
