Main Content

spdiags

提取非零对角线并创建稀疏带状对角矩阵

全页折叠

语法

Bout = spdiags(A)
[Bout,id] = spdiags(A)
Bout = spdiags(A,d)
S = spdiags(Bin,d,m,n)
S = spdiags(Bin,d,A)

说明

示例

Bout = spdiags(A) 从 m×n 矩阵 A 中提取非零对角线，并将其作为 min(m,n)×p 矩阵 Bout 中的列返回，其中 p 是非零对角线的数目。

示例

[Bout,id] = spdiags(A) 还返回 A 中非零对角线的对角线编号 id。Bout 的大小为 min(m,n)×length(id)。

示例

Bout = spdiags(A,d) 提取由 d 指定的 A 的对角线，并将其作为 min(m,n)×length(d) 矩阵 Bout 的列返回。

示例

S = spdiags(Bin,d,m,n) 通过获取 Bin 的列并沿 d 指定的对角线放置它们，来创建一个 m×n 稀疏矩阵 S。

示例

S = spdiags(Bin,d,A) 将 d 指定的 A 中的对角线替换为 Bin 的列。

示例

全部折叠

打开实时脚本

创建一个三对角矩阵，更改一些矩阵对角线，然后提取对角线。

使用对角线元素的 1×3 向量创建一个 9×9 三对角矩阵。查看矩阵元素。 

n = 9;
A = spdiags([1 -2 1],-1:1,n,n);
full(A)
ans = 9×9

    -2     1     0     0     0     0     0     0     0
     1    -2     1     0     0     0     0     0     0
     0     1    -2     1     0     0     0     0     0
     0     0     1    -2     1     0     0     0     0
     0     0     0     1    -2     1     0     0     0
     0     0     0     0     1    -2     1     0     0
     0     0     0     0     0     1    -2     1     0
     0     0     0     0     0     0     1    -2     1
     0     0     0     0     0     0     0     1    -2

更改 A 的主对角线 (d = 0) 上的值。

Bin = abs(-(n-1)/2:(n-1)/2)';
d = 0;
A = spdiags(Bin,d,A);
full(A)
ans = 9×9

     4     1     0     0     0     0     0     0     0
     1     3     1     0     0     0     0     0     0
     0     1     2     1     0     0     0     0     0
     0     0     1     1     1     0     0     0     0
     0     0     0     1     0     1     0     0     0
     0     0     0     0     1     1     1     0     0
     0     0     0     0     0     1     2     1     0
     0     0     0     0     0     0     1     3     1
     0     0     0     0     0     0     0     1     4

最后，将 A 的对角线恢复为矩阵中的列。

Bout = spdiags(A)
Bout = 9×3

     1     4     0
     1     3     1
     1     2     1
     1     1     1
     1     0     1
     1     1     1
     1     2     1
     1     3     1
     0     4     1
打开实时脚本

提取矩阵的非零对角线，并检查 spdiags 的输出格式。

创建同时包含非零对角线和零对角线的矩阵。

A = [0     5     0    10     0     0
     0     0     6     0    11     0
     3     0     0     7     0    12
     1     4     0     0     8     0
     0     2     5     0     0     9];

从该矩阵中提取非零对角线。指定两个输出以返回对角线编号。

[Bout,d] = spdiags(A)
Bout = 5×4

     0     0     5    10
     0     0     6    11
     0     3     7    12
     1     4     8     0
     2     5     9     0


d = 4×1

    -3
    -2
     1
     3

第一个输出 Bout 的列包含 A 的非零对角线。第二个输出 d 列出 A 的非零对角线的索引。A 中最长的非零对角线在 Bout 的第 3 列中。为了使 Bout 的所有列具有相同长度，A 的其他非零对角线在 Bout 中的对应列会用额外的零补足。对于 m < n 的 m×n 矩阵，规则如下：

  • 对于位于 A 的主对角线下方的非零对角线，在列的顶部添加额外零（如 Bout 的前两列中）。

  • 对于位于 A 的主对角线上方的非零对角线，在列的底部添加额外零（如 Bout 的最后一列中）。

即使在 Bout 中未返回最长的对角线，spdiags 仍会以这种方式用零填充 Bout。

打开实时脚本

创建 5×5 随机矩阵。

A = randi(10,5,5)
A = 5×5

     9     1     2     2     7
    10     3    10     5     1
     2     6    10    10     9
    10    10     5     8    10
     7    10     9    10     7

提取主对角线及位于它上方和下方的第一条对角线。

d = [-1 0 1];
Bout = spdiags(A,d)
Bout = 5×3

    10     9     0
     6     3     1
     5    10    10
    10     8    10
     0     7    10

尝试提取第五个上对角线 (d = 5)。由于 A 只有四条上对角线，因此 spdiags 将该对角线以全零形式返回，其长度与主对角线 (d = 0) 相同。

B5 = spdiags(A,5)
B5 = 5×1

     0
     0
     0
     0
     0
打开实时脚本

了解当输入矩阵的列比其替换的对角线长时，spdiags 如何创建对角线。

创建一个由数字 1 到 6 组成的 6×7 矩阵。

Bin = repmat((1:6)',[1 7])
Bin = 6×7

     1     1     1     1     1     1     1
     2     2     2     2     2     2     2
     3     3     3     3     3     3     3
     4     4     4     4     4     4     4
     5     5     5     5     5     5     5
     6     6     6     6     6     6     6

使用 spdiags 创建 6×6 方阵，以 Bin 的几个列为对角线。由于有些对角线只有一个或两个元素，因此 Bin 中的列和 A 中的对角线在大小上不匹配。

d = [-4 -2 -1 0 3 4 5];
A = spdiags(Bin,d,6,6);
full(A)
ans = 6×6

     1     0     0     4     5     6
     1     2     0     0     5     6
     1     2     3     0     0     6
     0     2     3     4     0     0
     1     0     3     4     5     0
     0     2     0     4     5     6

Bin 中的每列都有六个元素，但 A 中只有主对角线有六个元素。因此，A 中的所有其他对角线都会截断 Bin 的列中的元素，以使它们适合所选对角线：

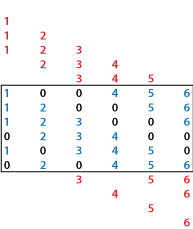
spdiags 截断对角线的方式取决于 m×n 矩阵 A 的大小。当 m≥n 时，行为如上图所示：

  • 位于主对角线下方的对角线首先从列的顶部获取元素。

  • 位于主对角线上方的对角线首先从列的底部获取元素。

当 m<n 时，此行为反向变化：

A = spdiags(Bin,d,5,6);
full(A)
ans = 5×6

     1     0     0     1     1     1
     2     2     0     0     2     2
     3     3     3     0     0     3
     0     4     4     4     0     0
     5     0     5     5     5     0

  • 位于主对角线上方的对角线首先从列的顶部获取元素。

  • 位于主对角线下方的对角线首先从列的底部获取元素。

输入参数

全部折叠

输入矩阵。此矩阵通常（但不一定）是稀疏矩阵。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
复数支持: 是

对角线编号，指定为由正整数组成的标量或向量。对角线编号遵循与 diag 相同的约定：

  • d < 0 位于主对角线下方，满足 d >= -(m-1)。

  • d = 0 是主对角线。

  • d > 0 位于主对角线上方，满足 d <= (n-1)。

m×n 矩阵 A 有 (m + n - 1) 条对角线。可在向量 d 中使用从 -(m-1) 到 (n-1) 的索引指定这些对角线。例如，如果 A 为 5×6 矩阵，则它有 10 条对角线，并使用索引 –4、–3、…、4、5 等在向量 d 中指定它们。下图说明这种对角线编号。

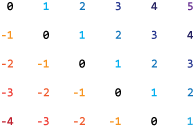
5-by-6 matrix. The main diagonal is labeled as zero, diagonals above it are labeled 1 to 5, and diagonals below it are labeled -1 to -4.

如果您指定位于 A 之外的对角线（如上面示例中的 d = 7），则 spdiags 以全零形式返回该对角线。

示例: spdiags(A,[3 5]) 从 A 中提取第三条和第五条对角线。

对角线元素，指定为标量、向量或矩阵。此参量通常（但不一定）是满矩阵。spdiags 使用 Bin 的列替换 A 中的指定对角线。如果请求的输出大小是 m×n，并且 Bin 是列向量或矩阵，则 Bin 必须有至少 min(m,n) 行。

使用语法 S = spdiags(Bin,d,m,n) 时，如果 Bin 的列具有的元素多于它要替换的对角线元素，并且 m >= n，则 spdiags 从 Bin 的列的下部获取上对角线元素，并从 Bin 的列的上部获取下对角线元素。但如果 m < n，则从 Bin 的列的上部获取上对角线元素并从下部获取下对角线元素。有关此行为的示例，请参阅不同大小的列和对角线。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
复数支持: 是

维度大小，指定为非负整数标量。spdiags 使用这些输入来确定要创建多大的矩阵。

示例: spdiags(Bin,d,300,400) 创建 300×400 矩阵，其中 B 的列沿指定的对角线 d 放置。

输出参量

全部折叠

对角线元素，以满矩阵形式返回。Bout 的列包含从 A 提取的对角线。对应于 A 的外部位置的任何 Bout 元素都设置为零。

对角线编号，以列向量形式返回。有关对角线编号的说明，请参阅 d。

输出矩阵。S 采用以下两种形式之一：

  • 使用 S = spdiags(Bin,d,A) 时，用 Bin 中的列替换 A 中的指定对角线，以创建 S。

  • 使用 S = spdiags(Bin,d,m,n) 时，通过获取 Bin 的列并沿 d 指定的对角线放置它们，来创建一个 m×n 稀疏矩阵 S。

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

在 R2006a 之前推出

全部展开

另请参阅

|