BLDC HDL

具有梯形磁通分布的三相无刷直流电机

自 R2023b 起

全页展开

库:
Motor Control Blockset HDL Support / Electrical Systems / Motors

描述

BLDC 模块实现三相无刷直流 (BLDC) 电机，其梯形反电动势在电相位差为 120 度的位置范围内保持恒定。该模块使用三相输入电压来调节各相电流，从而控制电机转矩或转速。

电机构造

此图显示具有单个极对的电机。

永磁体产生的转子磁场会随着电机角度的变化而产生梯形磁通变化率。

对于轴约定，当电机角度 θ_r 为零时，相位 a 与 d 轴对齐。

三相正弦模型电气系统

该模块使用由以下变换方程定义的 d’q’ 参考系，而不是标准的 dq 参考系。

$v_{d'} = \frac{2}{3} ((v_{a} - R i_{a} - E_{a}) \cos θ_{e} + (v_{b} - R i_{b} - E_{b}) \cos (θ_{e} - \frac{2 π}{3}) + (v_{c} - R i_{c} - E_{c}) \cos (θ_{e} + \frac{2 π}{3}))$

$v_{q'} = - \frac{2 π}{3} ((v_{a} - R i_{a} - E_{a}) \sin θ_{e} + (v_{b} - R i_{b} - E_{b}) \sin (θ_{e} - \frac{2 π}{3}) + (v_{c} - R i_{c} - E_{c}) \sin (θ_{e} + \frac{2 π}{3}))$

$\begin{array}{l} E_{a} = P ω_{m} \frac{\partial ψ_{a}}{\partial θ_{e}} \\ E_{b} = P ω_{m} \frac{\partial ψ_{b}}{\partial θ_{e}} \\ E_{c} = P ω_{m} \frac{\partial ψ_{c}}{\partial θ_{e}} \end{array}$

$\begin{array}{l} i_{a} = i_{d'} \cos θ_{e} - i_{q'} \sin θ_{e} \\ i_{b} = i_{d'} \cos (θ_{e} - \frac{2 π}{3}) - i_{q'} \sin (θ_{e} - \frac{2 π}{3}) \\ i_{c} = i_{d'} \cos (θ_{e} + \frac{2 π}{3}) - i_{q'} \sin (θ_{e} + \frac{2 π}{3}) \end{array}$

该模块实现以下在 BLDC 电机的 dq 和 d’q’ 参考系中表示的方程。电机参考系中的所有量都与定子相位 A 相关。

$\begin{array}{l} ω_{e} = P ω_{m} \\ \frac{d}{d t} i_{d'} = \frac{1}{L_{d}} v_{d'} + \frac{L_{q}}{L_{d}} P ω_{m} i_{q'} \end{array}$

$\frac{d}{d t} i_{q'} = \frac{1}{L_{q}} v_{q'} - \frac{L_{d}}{L_{q}} P ω_{m} i_{d'}$

$T_{e} = 1.5 P ((L_{d} - L_{q}) i_{d'} i_{q'}) + P (\frac{\partial ψ_{a}}{\partial θ_{e}} i_{a} + \frac{\partial ψ_{b}}{\partial θ_{e}} i_{b} + \frac{\partial ψ_{c}}{\partial θ_{e}} i_{c})$

下表描述了在这些方程中使用的变量。

L_q , L_d	q 轴和 d 轴电感 (H)
R	定子绕组的电阻（欧姆）
i_q' , i_d'	q' 轴和 d' 轴电流 (A)
v_q' , v_d'	q' 轴和 d' 轴电压 (V)
ω_m	电机的机械角速度（弧度/秒）
ω_e	电机的电气角速度（弧度/秒）
P	极对数
T_e	电磁转矩 (Nm)
θ_e	电气角（弧度）
v_a , v_b , v_c	定子相位 A、B 和 C 电压 (V)
i_a , i_b , i_c	定子相位 A、B 和 C 电流 (A)
E_a , E_b , E_c	定子相位 A、B 和 C 的反电动势 (V/m/s)
ψ_a , ψ_b , ψ_c	链接每个定子绕组的总磁通 (Wb)

机械系统

电机角速度由下式给出：

$\begin{matrix} \frac{d}{d t} ω_{m} = \frac{1}{J} (T_{e} - T_{f} - F ω_{m} - T_{m}) \\ \frac{d θ_{m}}{d t} = ω_{m} \end{matrix}$

上述方程用到了以下变量。

J	电机和负载的组合惯量 (kgm^2)
F	电机和负载的组合粘性摩擦（N·m/（弧度/秒））
θ_m	电机机械角位置（弧度）
T_m	电机轴转矩 (Nm)
T_e	电磁转矩 (Nm)
T_f	电机轴静态摩擦转矩 (Nm)
ω_m	电机的机械角速度（弧度/秒）

梯形磁通变化率

永磁体产生的转子磁场会随着转子角度的变化而产生梯形磁通变化率。此图显示三相 BLDC 电机三个相位的磁通变化率。

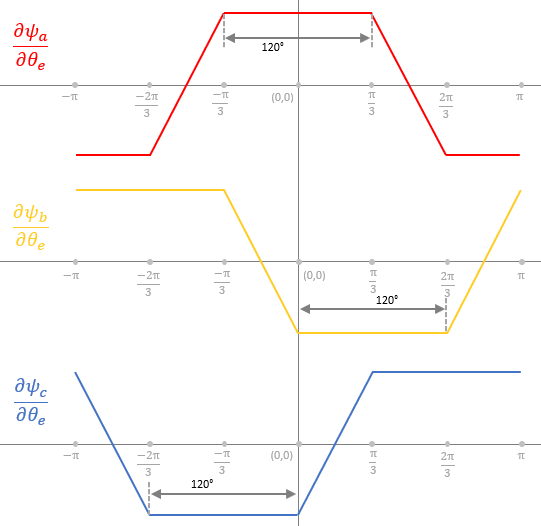
示例

使用传感器反馈对 BLDC 电机进行六步换相

使用六步换相法来控制三相 BLDC 电机的转速和旋转方向。

打开模型

端口

输入

全部展开

Config — 模块配置信号
矢量

包含模块配置参数的 BLDC HDL 模块的配置信号。有关组成参数的详细信息，请参阅 BLDC Configuration 模块中的配置输出端口描述。

数据类型: single

PhaseVolt — 定子端电压
`1`×`3` 数组

定子端电压 V_a、V_b 和 V_c，以 V 为单位。

数据类型: single

LdTrq/Spd — 电机上的负载转矩或电机轴的转速
标量

根据多路复用配置输入中可用的端口配置参数定义的工作模式，该端口支持以下输入之一：

T_m - 电机轴上的负载转矩，以 N·m 为单位。
ω_m - 电机的角速度，以弧度/秒为单位。

数据类型: single

Reset — 重置总线信号
标量

总线信号，模块用它来重置内部积分器。

数据类型: Boolean

输出

全部展开

Info — 总线信号
总线

总线信号包含以下模块计算。

信号	描述	变量	单位
`IaStator`	定子相电流 A	i_a	A
`IbStator`	定子相电流 B	i_b	A
`IcStator`	定子相电流 C	i_c	A
`IdSync`	d' 轴电流	i_d'	A
`IqSync`	q' 轴电流	i_q'	A
`VdSync`	d' 轴电压	v_d'	V
`VqSync`	q' 轴电压	v_q'	V
`MtrSpd`	电机的机械角速度	ω_m	弧度/秒
`MtrPos`	电机的机械角位置	θ_m	弧度
`MtrTrq`	电磁转矩	T_e	N·m
`MtrHall`	霍尔传感器输出	-	-
`BackEMF`	电机中生成的反电动势	E_a , E_b , E_c	V/m/s

PhaseCurr — a、b、c 相电流
1×3 数组

a、b、c 相电流分别为 i_a 、i_b 和 i_c ，以 A 为单位。

Torque — 电机转矩
`scalar`

电机转矩 T_mtr，以 N·m 为单位。

Speed — 电机转速
`scalar`

电机的角速度 ω_mtr，以弧度/秒为单位。

MtrElecAngle — 电机电角
标量

电机的电气位置 θ_e，以弧度为单位。

数据类型: single

参数

全部展开

采样时间(秒) — 模块的采样时间
`1e-6` (默认) | 标量

连续的模块执行实例之间的固定时间间隔（以秒为单位）。您也可以使用 -1 从输入信号继承采样时间。

扩展功能

HDL 代码生成
使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 VHDL、Verilog 和 SystemVerilog 代码。

HDL Coder™ 提供了影响 HDL 实现和综合逻辑的额外配置选项。

HDL 架构

此模块具有一个默认 HDL 架构。

HDL 模块属性


ConstrainedOutputPipeline	要通过移动设计中的现有延迟来放置在输出端的寄存器的数量。分布式流水线不会重新分布这些寄存器。默认值为 `0`。有关更多详细信息，请参阅 ConstrainedOutputPipeline (HDL Coder)。
InputPipeline	要在生成的代码中插入的输入流水线阶段数。分布式流水线和受限输出流水线可以移动这些寄存器。默认值为 `0`。有关更多详细信息，请参阅 InputPipeline (HDL Coder)。
OutputPipeline	要在生成的代码中插入的输出流水线阶段数。分布式流水线和受限输出流水线可以移动这些寄存器。默认值为 `0`。有关更多详细信息，请参阅 OutputPipeline (HDL Coder)。

BLDC HDL

描述