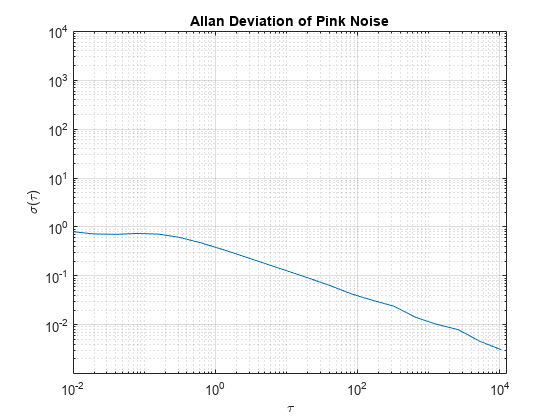
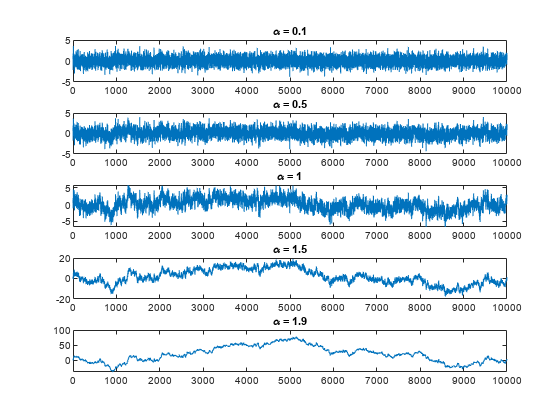
fractalcoef
Description
coeffs = fractalcoeffilter.
Tip
You can use the generated coefficients to specify the
BiasInstabilityCoefficients property of the accelparams, gyroparams, or magparams object.
Examples
Input Arguments
Output Arguments
References
[1] Kasdin, N. J. “Discrete Simulation of Colored Noise and Stochastic Processes and 1/fα Power Law Noise Generation.” Proceedings of the IEEE, vol. 83, no. 5, May 1995, pp. 802–27.
Extended Capabilities
Version History
Introduced in R2023b