使用优化变量拟合 ODE 参数
此示例说明如何使用优化变量(基于问题的方法)以最小二乘方式查找优化常微分方程 (ODE) 的参数。
问题
问题是涉及几种物质的多步响应模型,其中一些物质相互反应以产生不同的物质。
对于此问题,真实的反应速率是未知的。因此,您需要观测反应并推断速率。假设您可以测量一组时间 内的物质。根据这些观测值,对测量值进行最佳反应速率组拟合。
模型
该模型包含六种物质 到 ,反应如下:
一个 和一个 以速率 反应形成一个
一个 和一个 以速率 反应形成一个
一个 和一个 以速率 反应形成一个
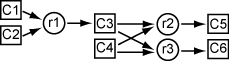
反应速率与所需物质数量的乘积成正比。因此,如果 表示物质 的量,则生成 的反应速率就是 。类似地,生成 的反应速率是 ,生成 的反应速率是 。
换句话说,控制系统演化的微分方程是
在时间点 0 处的点 处开始微分方程。这些初始值确保所有物质都完全反应,生成的 到 随着时间的增加接近于零。
在 MATLAB 中表示模型
diffun 函数以一种适合用 ode45 求解的形式实现微分方程。
type diffunfunction dydt = diffun(~,y,r) dydt = zeros(6,1); s12 = y(1)*y(2); s34 = y(3)*y(4); dydt(1) = -r(1)*s12; dydt(2) = -r(1)*s12; dydt(3) = -r(2)*s34 + r(1)*s12 - r(3)*s34; dydt(4) = -r(2)*s34 - r(3)*s34; dydt(5) = r(2)*s34; dydt(6) = r(3)*s34; end
真实的反应速率是 、 和 。通过调用 ode45 计算系统从时间 0 到 5 的演化。
rtrue = [2.5 1.2 0.45]; y0 = [1 1 0 1 0 0]; tspan = linspace(0,5); soltrue = ode45(@(t,y)diffun(t,y,rtrue),tspan,y0); yvalstrue = deval(soltrue,tspan); for i = 1:6 subplot(3,2,i) plot(tspan,yvalstrue(i,:)) title(['y(',num2str(i),')']) end
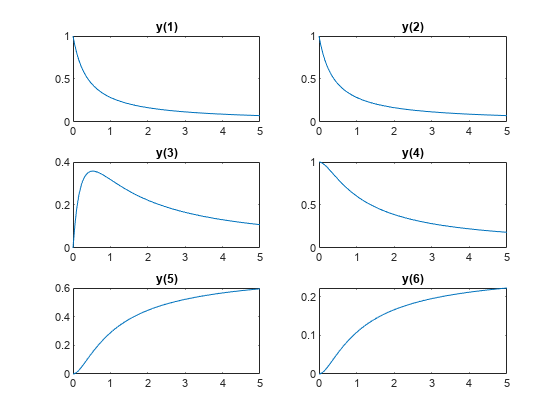
优化问题
为了准备问题以使用基于问题的方法得到解,请创建一个三元素优化变量 r,其下界为 0.1,上界为 10。
r = optimvar('r',3,"LowerBound",0.1,"UpperBound",10);
此问题的目标函数是具有参数 r 的 ODE 解和具有真实参数 yvals 的解之间的差的平方和。为了表达此目标函数,请首先编写一个 MATLAB 函数,该函数使用参数 r 来计算 ODE 解。此函数是 RtoODE 函数。
type RtoODEfunction solpts = RtoODE(r,tspan,y0) sol = ode45(@(t,y)diffun(t,y,r),tspan,y0); solpts = deval(sol,tspan); end
要在目标函数中使用 RtoODE,请使用 fcn2optimexpr 将函数转换为优化表达式。请参阅将非线性函数转换为优化表达式。
myfcn = fcn2optimexpr(@RtoODE,r,tspan,y0);
将目标函数表示为 ODE 解和具有真实参数的解之间的平方差之和。
obj = sum(sum((myfcn - yvalstrue).^2));
用目标函数 obj 创建一个优化问题。
prob = optimproblem("Objective",obj);求解问题
要找到最佳拟合参数 r,请为求解器提供初始估计值 r0,并调用 solve。
r0.r = [1 1 1]; [rsol,sumsq] = solve(prob,r0)
Solving problem using lsqnonlin. Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
rsol = struct with fields:
r: [3×1 double]
sumsq = 3.8678e-15
平方差之和实质上为零,这意味着求解器找到了使 ODE 解与具有真实参数的解匹配的参数。因此,与预期相符,解包含真实参数。
disp(rsol.r)
2.5000
1.2000
0.4500
disp(rtrue)
2.5000 1.2000 0.4500
有限的观测值
假设您无法观测到 y 的所有分量,而只能观测到最终输出 y(5) 和 y(6)。根据这些有限的信息,您能得到所有反应速率的值吗?
要找出答案,请修改函数 RtoODE 以仅返回第五和第六个 ODE 输出。修改后的 ODE 求解器在 RtoODE2 中。
type RtoODE2function solpts = RtoODE2(r,tspan,y0) solpts = RtoODE(r,tspan,y0); solpts = solpts([5,6],:); % Just y(5) and y(6) end
RtoODE2 函数会简单地调用 RtoODE,然后获取输出的最后两行。
基于 RtoODE2 和优化变量 r、时间跨度数据 tspan 和初始点 y0 创建一个新的优化表达式。
myfcn2 = fcn2optimexpr(@RtoODE2,r,tspan,y0);
修改比较数据,使其仅包括输出 5 和 6。
yvals2 = yvalstrue([5,6],:);
基于优化表达式 myfcn2 和比较数据 yvals2 创建一个新的目标和新的优化问题。
obj2 = sum(sum((myfcn2 - yvals2).^2));
prob2 = optimproblem("Objective",obj2);基于以下有限观测值集来求解问题。
[rsol2,sumsq2] = solve(prob2,r0)
Solving problem using lsqnonlin. Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance. <stopping criteria details>
rsol2 = struct with fields:
r: [3×1 double]
sumsq2 = 2.1616e-05
同样,返回的平方和实质上为零。这是否意味着求解器找到了正确的反应速率?
disp(rsol2.r)
1.7811
1.5730
0.5899
disp(rtrue)
2.5000 1.2000 0.4500
不是的;在这种情况下,新速率与真实速率相差很大。然而,与真实值相比的新 ODE 解的绘图显示 y(5) 和 y(6) 与真实值匹配。
figure plot(tspan,yvals2(1,:),'b-') hold on ss2 = RtoODE2(rsol2.r,tspan,y0); plot(tspan,ss2(1,:),'r--') plot(tspan,yvals2(2,:),'c-') plot(tspan,ss2(2,:),'m--') legend('True y(5)','New y(5)','True y(6)','New y(6)','Location','northwest') hold off

为了确定此问题的正确反应速率,您必须有比 y(5) 和 y(6) 更多的观测值数据。
用新参数绘制解的所有分量,用真实参数绘制解。
figure yvals2 = RtoODE(rsol2.r,tspan,y0); for i = 1:6 subplot(3,2,i) plot(tspan,yvalstrue(i,:),'b-',tspan,yvals2(i,:),'r--') legend('True','New','Location','best') title(['y(',num2str(i),')']) end

使用新参数时,物质 和 消耗得更慢,物质 不会累积那么多。但是,物质 、 和 在使用新参数和真实参数时都有完全相同的演化。
另请参阅
solve | ode45 | fcn2optimexpr