使用 arrayfun 提高 GPU 上元素级 MATLAB 函数的性能
此示例展示了如何通过使用 arrayfun 在 GPU 上运行 MATLAB® 函数来提高代码的性能。
当 MATLAB 函数包含许多逐元素操作时,使用 arrayfun 可以提供比使用 gpuArray 输入数据直接在 GPU 上执行 MATLAB 函数更好的性能。为了使函数与 arrayfun 兼容,它必须能够对输入数组的单个元素进行操作,以使用标量运算和算术计算输出数组的单个元素。
在此示例中,您可以比较在 CPU 上执行、在 GPU 上不使用 arrayfun 执行以及在 GPU 上使用 arrayfun 执行的函数的执行时间。
定义测试函数
根据狭义相对论原理,洛伦兹因子决定了物体在运动时其物理属性如何变化。对于相对于观察者以速度 移动的物体,洛伦兹因子 定义为
.
是 与 的比率,其中 是真空中的光速。示例末尾定义的 lorentz 函数按如下方式计算洛伦兹因子。
Y = 1./sqrt(1-B.*B);
为 GPU 执行准备函数
大多数 MATLAB 函数默认在 CPU 上执行。要在 GPU 上执行 lorentz,请提供 gpuArray 对象作为输入。gpuArray 对象表示存储在 GPU 内存中的数组。由于许多函数支持 gpuArray 输入,因此您通常可以在 GPU 上运行代码,而只需对代码进行最少的更改。有关详细信息,请参阅在 GPU 上运行 MATLAB 函数。
由于 lorentz 包含单独的元素操作,因此在 GPU 上一次执行一个操作不会带来显著的性能提升。您可以使用 lorentz 一次执行 arrayfun 函数中的所有操作来提高性能。
要使用 lorentz 在 GPU 上运行 arrayfun 函数,请定义该函数的句柄。
lorentzFcn = @lorentz;
设置比较参数
在此示例中,您将比较对包含 到 元素的数组执行的 lorentz 函数的执行时间。设置要运行的比较次数,以及传递给函数的数组大小的上限和下限。
numComp = 15; lowerLimit = 4; upperLimit = 8.5;
将要传递给函数的数组的大小指定为对数间距数组。此示例可能需要几分钟才能运行。为了减少执行时间,请减少数组大小的上限。
arraySize = ceil(logspace(lowerLimit,upperLimit,numComp));
CPU 和 GPU 上的执行时间
对不同的执行模式进行计时:
for i = 1:numComp fprintf('Timing function for input array of size %d \n', arraySize(i)); % Create random input data data = rand(arraySize(i),1,"single"); % CPU execution tcpu(i) = timeit(@() lorentzFcn(data)); % Send data to the GPU gdata = gpuArray(data); % GPU execution using only gpuArray objects tgpuObject(i) = gputimeit(@() lorentzFcn(gdata)); % GPU execution using gpuArray objects with arrayfun tgpuArrayfun(i) = gputimeit(@() arrayfun(lorentzFcn,gdata)); end
Timing function for input array of size 10000 Timing function for input array of size 20962 Timing function for input array of size 43940 Timing function for input array of size 92106 Timing function for input array of size 193070 Timing function for input array of size 404709 Timing function for input array of size 848343 Timing function for input array of size 1778280 Timing function for input array of size 3727594 Timing function for input array of size 7813708 Timing function for input array of size 16378938 Timing function for input array of size 34333201 Timing function for input array of size 71968568 Timing function for input array of size 150859071 Timing function for input array of size 316227767
比较结果
为了比较结果,请绘制执行时间与数据元素数量的关系图。
loglog(arraySize,[tgpuObject; tgpuArrayfun; tcpu]) xlabel("Input Array Size") ylabel("Execution Time (s)") legend(["GPU Execution" "GPU Execution with \fontname{courier}arrayfun" "CPU Execution"], ... location="southeast")

对于较小的数组,CPU 执行该函数的速度比 GPU 更快。随着输入数组的大小增加,GPU 的性能相对于 CPU 的性能有所提高。当数组大小超过阈值时,GPU 执行函数的速度比 CPU 更快。GPU 性能超过 CPU 性能的阈值取决于您使用的硬件和执行的函数。
分别计算 CPU 执行时间与 GPU 执行时间的比率以及使用 arrayfun 与 GPU 执行时间的比率。
gpuObjectSpeedup = tcpu./tgpuObject; gpuArrayfunSpeedup = tcpu./tgpuArrayfun;
绘制与输入数组大小相对应的比率。
semilogx(arraySize,[gpuObjectSpeedup;gpuArrayfunSpeedup]) xlabel("Input Array Size") ylabel("Ratio of CPU to GPU Execution Times") legend(["GPU Execution" "GPU Execution with \fontname{courier}arrayfun"],location="southeast")
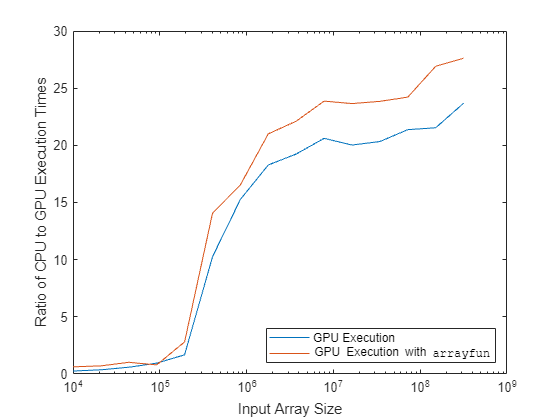
使用 lorentz 执行 arrayfun 始终比仅在 GPU 上执行更快。当您将本示例中描述的技术应用到您自己的代码中时,性能的提升将在很大程度上取决于您的硬件和您运行的代码。
支持函数
lorentz 函数采用 并根据以下方程计算洛伦兹因子
.
function Y = lorentz(B) Y = 1./sqrt(1-B.*B); end
另请参阅
arrayfun | gpuArray | gputimeit