使用 GPU `arrayfun` 进行蒙特卡罗仿真

打开实时脚本

此示例展示如何使用蒙特卡罗方法在 GPU 上计算金融期权的价格。

该示例使用了三种简单类型的奇异期权，但您可以采用类似的方式对更复杂的期权进行定价。在此示例中，您可以比较在 CPU 上运行蒙特卡罗仿真和在 GPU 上使用 arrayfun 所需的时间。

股票价格演变

假设价格根据与无风险利率、股息收益率（如果有）和市场波动相关的对数正态分布演变。此外，假设所有这些数量在期权的有效期内保持不变。这些假设导致了价格的随机微分方程。

$d S = S \times [(r - d) d t + σ ϵ \sqrt{d t}]$ ,

其中 $S$ 是股票价格， $r$ 是无风险利率， $d$ 是股票的年股息收益率， $σ$ 是价格波动率， $ϵ$ 表示高斯白噪声过程。假设 $(S + Δ S) / S$ 服从对数正态分布，则可将该微分方程离散化，得到该方程。

$S_{t + 1} = S_{t} \times \exp [(r - d - \frac{1}{2} σ^{2}) Δ t + σ ϵ \sqrt{Δ t}]$ 。

使用 100 美元的股票检查两年的时间窗口，并做出以下假设：

该股票每年产生 1% 的股息。
无风险政府利率为 0.5%。
价格按日采样，每年 250 个工作日。
市场波动率为每年 20%。

stockPrice = 100;
timeToExpiry = 2;
dividend = 0.01;
riskFreeRate = 0.005;
sampleRate = 1/250;
volatility = 0.20;

为了确保结果可预测，请为 CPU 和 GPU 随机数生成器设置种子。

seed = 1234;
rng(seed);
gpurng(seed);

仿真股票价格随时间的变化轨迹并绘制结果。

price = stockPrice;
time = 0;
h = animatedline(Marker=".");

while time < timeToExpiry
    time = time + sampleRate;
    drift = (riskFreeRate - dividend - volatility*volatility/2)*sampleRate;
    perturbation = volatility*sqrt(sampleRate)*randn;
    price = price*exp(drift + perturbation);
    addpoints(h,time,price);
end

grid on
axis tight
xlabel("Time (years)")
ylabel("Stock Price ($)")

Figure contains an axes object. The axes object contains an object of type animatedline.

CPU 和 GPU 上的执行时间

本示例末尾提供的 simulateStockPrice 函数使用上一节中描述的离散微分方程仿真股票价格。

准备运行 100,000 次股票价格蒙特卡罗仿真的输入数据。

N = 100000;
startStockPrices = stockPrice*ones(N,1);

在 CPU 上进行 100,000 次仿真。

tic
finalStockPricesCPU = zeros(N,1);
for i = 1:N
    finalStockPricesCPU(i) = simulateStockPrice(startStockPrices(i), ...
        riskFreeRate,dividend,volatility, ...
        timeToExpiry,sampleRate);
end
timeCPU = toc;

因为每个仿真都会对期权价格给出一个独立的估计，所以取平均值作为结果。

fprintf("Calculated average price of $%1.4f on the CPU in %1.3f secs.\n", ...
    mean(finalStockPricesCPU),timeCPU);

Calculated average price of $99.0857 on the CPU in 2.206 secs.

要在 GPU 上运行仿真，请通过创建 gpuArray 对象在 GPU 上准备输入数据。

gpuStartStockPrices = gpuArray(startStockPrices);

当您使用 GPU 数组和函数句柄作为输入调用 arrayfun 时，arrayfun 会将您指定的函数应用于数组的每个元素。这种行为意味着不需要循环遍历每个起始股票价格。GPU 上的 arrayfun 函数将逐元素的 MATLAB® 函数转变为自定义 CUDA® 内核，从而减少了执行操作的开销。

使用 simulateStockPrice 运行 arrayfun 函数，并使用 gputimeit 在 GPU 上计时 100,000 次仿真。

finalStockPricesGPU = arrayfun(@simulateStockPrice, ...
        gpuStartStockPrices,riskFreeRate,dividend,volatility, ...
        timeToExpiry,sampleRate);

timeGPU = gputimeit(@() arrayfun(@simulateStockPrice, ...
        gpuStartStockPrices,riskFreeRate,dividend,volatility, ...
        timeToExpiry,sampleRate));

fprintf("Calculated average price of $%1.4f on the GPU in %1.3f secs.\n", ...
    mean(finalStockPricesGPU),timeGPU);

Calculated average price of $99.0442 on the GPU in 0.023 secs.

以直方图形式绘制 GPU 上的蒙特卡罗仿真结果。

histogram(finalStockPricesGPU,100);
xlabel("Stock Price ($)")
ylabel("Frequency")
grid on

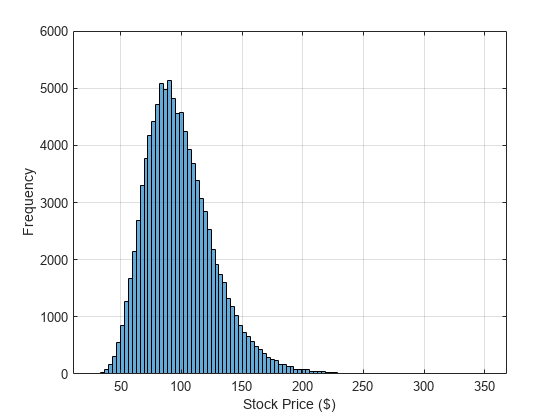
Figure contains an axes object. The axes object contains an object of type histogram.

亚式期权定价

使用基于期权有效期内股票价格算术平均值的欧式亚式期权。asianCallOption 函数通过累积仿真过程中的价格来计算平均价格。对于看涨期权，如果平均价格高于执行价格，该函数将行使该期权。赔付金额是平均价格与执行价格之间的差额。使用本示例末尾提供的 asianCallOption 来仿真亚式看涨期权。

将期权的执行价格设为 95 美元。

strike = 95;

使用 arrayfun 在 CPU 和 GPU 上进行 100,000 次仿真并显示结果。

tic
optionPricesCPU = zeros(N,1);
for i=1:N
    optionPricesCPU(i) = asianCallOption(startStockPrices(i), ...
        riskFreeRate,dividend,volatility,strike, ...
        timeToExpiry,sampleRate);
end
timeAsianOptionCPU = toc;

fprintf("Calculated average price of $%1.4f on the CPU in %1.3f secs.\n", ...
    mean(optionPricesCPU),timeAsianOptionCPU);

Calculated average price of $8.6733 on the CPU in 2.146 secs.

optionPricesGPU = arrayfun( @asianCallOption, ...
    gpuStartStockPrices,riskFreeRate,dividend,volatility,strike, ...
    timeToExpiry,sampleRate );

timeAsianOptionGPU = gputimeit(@() arrayfun( @asianCallOption, ...
    gpuStartStockPrices,riskFreeRate,dividend,volatility,strike, ...
    timeToExpiry,sampleRate));

fprintf("Calculated average price of $%1.4f on the GPU in %1.3f secs.\n", ...
    mean(optionPricesGPU),timeAsianOptionGPU );

Calculated average price of $8.7448 on the GPU in 0.023 secs.

回溯期权的定价

使用欧式回顾期权，其支出是期权有效期内最低股票价格与最终股票价格之间的差额。期权的执行价格是最低股票价格。由于最终股票价格总是大于或等于最低价，因此期权总是被行使，并不是真正可选的。使用本示例末尾提供的 lookbackCallOption 来仿真欧式回溯看涨期权。

使用 arrayfun 在 CPU 和 GPU 上进行 100,000 次仿真并显示结果。

tic
optionPricesCPU = zeros(N,1);
for i=1:N
    optionPricesCPU(i) = lookbackCallOption(startStockPrices(i), ...
        riskFreeRate,dividend,volatility, ...
        timeToExpiry,sampleRate);
end
timeLookbackOptionCPU = toc;

fprintf("Calculated average price of $%1.4f on the CPU in %1.3f secs.\n", ...
    mean(optionPricesCPU),timeLookbackOptionCPU);

Calculated average price of $19.2456 on the CPU in 2.201 secs.

optionPricesGPU = arrayfun(@lookbackCallOption, ...
    gpuStartStockPrices,riskFreeRate,dividend,volatility, ...
    timeToExpiry,sampleRate);

timeLookbackOptionGPU = gputimeit(@() arrayfun(@lookbackCallOption, ...
    gpuStartStockPrices,riskFreeRate,dividend,volatility, ...
    timeToExpiry,sampleRate));

fprintf("Calculated average price of $%1.4f on the GPU in %1.3f secs.\n", ...
    mean(optionPricesGPU),timeLookbackOptionGPU);

Calculated average price of $19.3893 on the GPU in 0.021 secs.

障碍期权的定价

使用上行障碍期权，如果股票价格达到障碍水平，该期权将失效。如果股价保持在障碍水平以下，则在正常的欧式看涨期权计算中使用最终股价。使用本示例末尾提供的 upAndOutCallOption 函数来仿真上行障碍看涨期权。

设定期权的执行价格以及期权失效的障碍价格。使用执行价格 95 美元和障碍价格 150 美元。

strike  = 95;
barrier = 150;

使用 arrayfun 在 CPU 和 GPU 上进行 100,000 次仿真并显示结果。

tic
optionPricesCPU = zeros(N,1);
for i=1:N
    optionPricesCPU(i) = upAndOutCallOption(startStockPrices(i), ...
        riskFreeRate,dividend,volatility,strike, ...
        barrier,timeToExpiry,sampleRate);
end
timeBarrierOptionCPU = toc;

fprintf("Calculated average price of $%1.4f on the CPU in %1.3f secs.\n", ...
    mean(optionPricesCPU),timeBarrierOptionCPU);

Calculated average price of $6.8327 on the CPU in 2.074 secs.

optionPricesGPU = arrayfun(@upAndOutCallOption, ...
    gpuStartStockPrices,riskFreeRate,dividend,volatility,strike, ...
    barrier,timeToExpiry,sampleRate);

timeBarrierOptionGPU = gputimeit(@() arrayfun(@upAndOutCallOption, ...
    gpuStartStockPrices,riskFreeRate,dividend,volatility,strike, ...
    barrier,timeToExpiry,sampleRate));

fprintf("Calculated average price of $%1.4f on the GPU in %1.3f secs.\n", ...
    mean(optionPricesGPU),timeBarrierOptionGPU);

Calculated average price of $6.7834 on the GPU in 0.021 secs.

比较结果

计算每次仿真的 CPU 执行时间与 GPU 执行时间的比率。

ratio = [timeCPU/timeGPU timeAsianOptionCPU/timeAsianOptionGPU ...
    timeLookbackOptionCPU/timeLookbackOptionGPU timeBarrierOptionCPU/timeBarrierOptionGPU]

ratio = 1×4

   94.2557   94.6009  104.1725   97.5490

为了直观地显示结果，绘制每次仿真的执行时间比率。

bar(categorical(["Stock Price" "Asian Call Option" "Lookback Option" "Barrier Option"]), ...
    ratio)
ylabel("Ratio of CPU to GPU Execution Time")

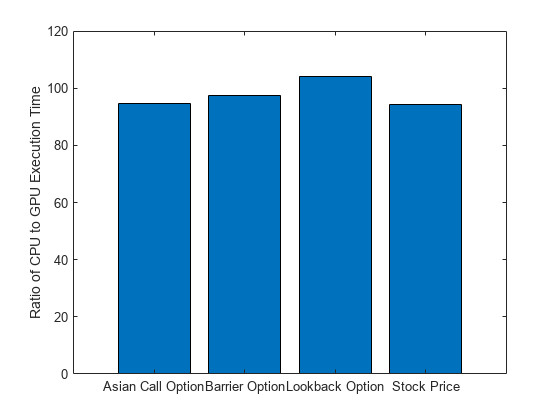
Figure contains an axes object. The axes object contains an object of type bar.

在此示例中，使用 arrayfun 在 GPU 上运行仿真比在 CPU 上运行仿真要快得多。

当您将本示例中描述的技术应用到您自己的代码中时，性能的提升将在很大程度上取决于您的硬件和您运行的代码。

支持函数

股价演变仿真函数

simulateStockPrice 函数执行蒙特卡罗仿真以确定最终股票价格。该计算假设价格根据与无风险利率、股息收益率（如果有）和市场波动相关的对数正态分布演变。

simulateStockPrice 函数以初始股票价格、无风险利率、股息率、市场波动率、总时间窗口和采样率作为输入。

function finalStockPrice = simulateStockPrice(price,riskFreeRate,dividend,volatility,T,dT)
t = 0;
while t < T
    t = t + dT;
    drift = (riskFreeRate - dividend - volatility*volatility/2)*dT;
    perturbation = volatility*sqrt(dT)*randn;
    price = price.*exp(drift + perturbation);
end

finalStockPrice = price;
end

亚式看涨期权函数

asianCallOption 函数执行蒙特卡罗仿真来确定亚式看涨期权价格。该计算假设价格根据与无风险利率、股息收益率（如果有）和市场波动相关的对数正态分布演变。该函数通过累积仿真期间的价格来计算平均价格。对于看涨期权，如果平均价格高于执行价格，该函数将行使该期权。赔付金额是平均价格与执行价格之间的差额。

asianCallOption 函数以初始股票价格、无风险利率、股息率、市场波动率、执行价格、总时间窗口和采样率作为输入。

function optionPrice = asianCallOption(price,riskFreeRate,dividend,volatility,strike,T,dT)
t = 0;
cumulativePrice = 0;
while t < T
    t = t + dT;
    dr = (riskFreeRate - dividend - volatility*volatility/2)*dT;
    pert = volatility*sqrt(dT)*randn;
    price = price*exp(dr + pert);
    cumulativePrice = cumulativePrice + price;
end
numSteps = (T/dT);
meanPrice = cumulativePrice/numSteps;

% Express the final price in today's money
optionPrice = exp(-riskFreeRate*T)*max(0,meanPrice - strike);
end

回望期权函数

lookbackCallOption 函数执行蒙特卡罗仿真以确定欧式回顾期权，其支出是期权有效期内最低股票价格和最终股票价格之间的差额。期权的执行价格是最低股票价格。由于最终股票价格总是大于或等于最低价，因此期权总是被行使，并不是真正“可选”的。

lookbackCallOption 函数以初始股票价格、无风险利率、股息率、市场波动率、总时间窗口和采样率作为输入。

function optionPrice = lookbackCallOption(price,riskFreeRate,dividend,volatility,T,dT)
t = 0;
minPrice = price;
while t < T
    t = t + dT;
    dr = (riskFreeRate - dividend - volatility*volatility/2)*dT;
    pert = volatility*sqrt(dT)*randn;
    price = price*exp(dr + pert);
    if price < minPrice
        minPrice = price;
    end
end

% Express the final price in today's money
optionPrice = exp(-riskFreeRate*T)*max(0,price - minPrice);
end

障碍期权函数

upAndOutCallOption 函数执行蒙特卡罗仿真来确定上行障碍看涨期权价格。如果股票价格保持在障碍水平以下，该函数将使用正常欧式看涨期权计算中的最终股票价格。

upAndOutCallOption 函数以初始股票价格、无风险利率、股息率、市场波动率、执行价格、障碍价格、总时间窗口和采样率作为输入。

function optionPrice = upAndOutCallOption(price,riskFreeRate,dividend,volatility,strike,barrier,T,dT)
t = 0;
while (t < T) && (price < barrier)
    t = t + dT;
    dr = (riskFreeRate - dividend - volatility*volatility/2)*dT;
    pert = volatility*sqrt(dT)*randn;
    price = price*exp(dr + pert);
end

if price<barrier
    % Within barrier, so price as for a European option
    optionPrice = exp(-riskFreeRate*T)*max(0,price - strike);
else
    % Hit the barrier, so the option is withdrawn
    optionPrice = 0;
end
end

另请参阅

arrayfun | gpuArray | gputimeit

主题

测量并提高 GPU 性能
使用 arrayfun 提高 GPU 上元素级 MATLAB 函数的性能
Pricing European and American Spread Options (Financial Instruments Toolbox)
Pricing Asian Options (Financial Instruments Toolbox)
Pricing European Call Options Using Different Equity Models (Financial Instruments Toolbox)
Supported Equity Derivative Functions (Financial Instruments Toolbox)

使用 GPU arrayfun 进行蒙特卡罗仿真

股票价格演变

CPU 和 GPU 上的执行时间

亚式期权定价

回溯期权的定价

障碍期权的定价

比较结果

支持函数

股价演变仿真函数

亚式看涨期权函数

回望期权函数

障碍期权函数

另请参阅

主题

使用 GPU `arrayfun` 进行蒙特卡罗仿真