使用 ValueStore 监控蒙特卡罗批处理作业

打开实时脚本

此示例显示如何使用 ValueStore 在执行期间监控蒙特卡罗批处理作业。

所有作业都有一个关联的 ValueStore 对象，您可以在作业运行时使用该对象访问数据。您可以在作业运行时继续使用命令行。此示例展示如何在作业运行时使用 ValueStore 对象访问和监控批量蒙特卡罗仿真的数据。

使用蒙特卡罗估计 π

您可以使用多种蒙特卡罗方法估算 π 的值。此示例说明如何用简单的蒙特卡罗面积方法估计 π。

要使用蒙特卡罗面积方法估计 π，请执行以下步骤：

从均匀分布中随机生成一个点的 $x$ 和 $y$ 坐标。
确定该点是否位于正方形的内接圆内。更新圆内的点数和总点数。
根据需要重复以优化估算。

有关更多详细信息，请参阅示例的简单蒙特卡罗面积方法部分。

并行运行多个仿真并将中间结果作为键值条目存储在作业 ValueStore 对象中。使用 updatePlot 辅助函数检索和处理来自 ValueStore 对象的结果并更新图以监控仿真的进度。

准备图来可视化中期结果

指定圆的半径和作业迭代的 parfor 循环次数。

r = 1;
steps = 200;

创建两个图来可视化蒙特卡罗仿真的中期结果。包括标题、标签和限制等设置。设置轴的纵横比，以便它们在仿真过程中自动更新时不会改变。

fig1 = figure(Name="Estimate Pi with Monte Carlo",Visible="on");
ax1 = gca(fig1);
theta = linspace(0,2*pi);
m = cos(theta);
n = sin(theta);
plot(ax1,m,n,"k")
xlabel(ax1,"Value of $x$",Interpreter="latex");
ylabel(ax1,"Value of $y$",Interpreter="latex");
title(ax1,"Randomly Generated Points in Circle",Interpreter="latex");

axis(ax1,"equal",[-1 1 -1 1])

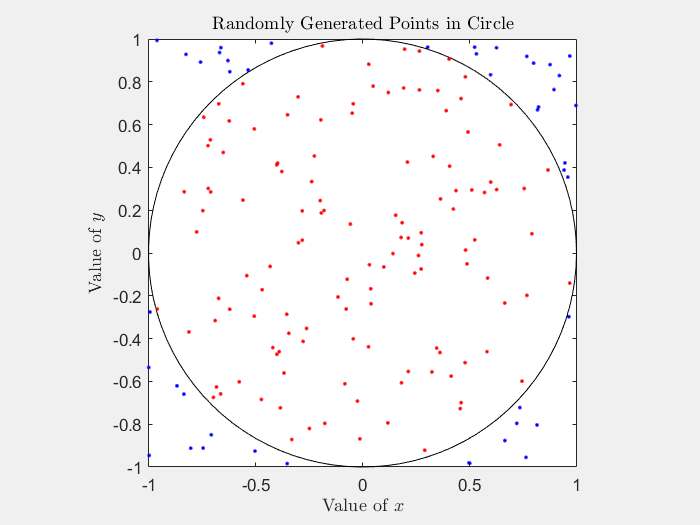
fig2 = figure(Name="Current Pi Estimate",Visible="on");
ax2 = gca(fig2);
xlabel(ax2,"Steps",Interpreter="latex");
ylabel(ax2,"Estimate of $\pi$",Interpreter="latex");
title(ax2,"Current Estimate of $\pi$",Interpreter="latex");
xlim(ax2,([0 steps]))
ylim(ax2,([0 4]))

设置并提交批处理作业

从默认集群并行环境中创建一个集群对象。要检查默认并行环境，在 MATLAB® 主页选项卡中的环境部分，点击并行，然后将鼠标悬停在选择并行环境上。

cluster = parcluster;

示例末尾定义的 GeneratePoints 函数包含蒙特卡罗仿真定义。使用 batch 通过输入参量 GeneratePoints 和 r 卸载 steps 中的计算。使用 Pool 名称-值参量创建一个具有四个工作单元的并行池。由于 batch 函数使用另一个工作单元来运行该函数，因此请确保请求的池工作单元数量比集群中可用的工作单元数量少一个。

job = batch(cluster,@generatePoints,1,{r,steps},Pool=4);

设置 KeyUpdatedFcn 回调。获取作业的 ValueStore 对象，并设置一个回调函数，当作业向 ValueStore 对象添加条目时执行。

当作业在每个 UpdatePlot 循环中向 ValueStore 对象添加一个条目时，parfor 回调函数就会运行。此函数使用新数据更新图。

该作业可以在软件设置 ValueStore 回调之前将信息写入 KeyUpdatedFcn 对象。为了通过在提交作业之前设置 KeyUpdatedFcn 回调来防止此行为，请使用 createCommunicatingJob函数。

store = job.ValueStore;
store.KeyUpdatedFcn = @(store,key) updatePlot(ax1,ax2,store,key);

使用 wait 在实时脚本中维持与作业的活动连接。使用 wait 代码块会在作业运行时阻止命令行。或者，从 MATLAB 命令行调用此示例的纯脚本版本，以便在执行期间使用命令行。绘图可能需要很长时间才能更新。

disp("Waiting for job to finish ...")

Waiting for job to finish ...

wait(job);
disp("Job completed")

Job completed

作业完成后，您仍然可以访问作业 ValueStore 对象。您可以使用键访问来自 ValueStore 对象的数据。例如，查看步骤 6 的数据。

disp("Fetching example result for step 6:")

Fetching example result for step 6:

resultFromStep6 = store("Step 6")

resultFromStep6 = struct with fields:
           step: 6
              x: 0.9460
              y: 0.4209
      in_circle: 0
    point_color: 'b'

检索作业的结果然后删除该作业。

pointsData = fetchOutputs(job);
delete(job)
clear job

支持函数

蒙特卡罗仿真

generatePoints 函数随机将点放置在正方形中。函数使用 rand 从区间（-r, r）内的均匀分布生成两个随机数 $x$ 和 $y$ 。然后，该函数确定由 $x$ 和 $y$ 的值定义的点是否在圆内，并使用唯一键将 $x$ 和 $y$ 的值存储在作业 ValueStore 对象中。如果该点位于圆圈内，该函数将为该条目分配值 1 并将颜色设为红色。如果该点位于圆外，该函数将为该条目分配 0 值和蓝色。ValueStore 对象在 parfor 循环的每次迭代中都会获得一个新条目。将结果保存在分段变量 points 中，您可以将其作为作业的属性来访问。

function points = generatePoints(r,steps)
points = zeros(steps,4);
parfor idx = 1:steps
    x = (r+r)*rand - r;
    y = (r+r)*rand - r;
    pause(2) % Use pause to control the speed of the example.
    if sqrt(x^2 + y^2) < r
        points(idx,:,end) = [idx x y 1];
        point_color = 'r';
        in_circle = 1
    else
        points(idx,:,end) = [idx x y 0];
        point_color = 'b';
        in_circle = 0
    end

    % Get the ValueStore object of the current job.
    store = getCurrentValueStore;
    % Store the simulation results in the 
    % job ValueStore object with a unique key.
    key = "Step " + idx;
    store(key) = struct(step=idx,x=x,y=y, ...
        in_circle=in_circle,point_color=point_color);
end
end

实时更新结果

使用中间结果图来监控蒙特卡罗 π 估计的进度。每次作业更新 updatePlot 对象时，ValueStore 函数都会更新图。

function updatePlot(ax1,ax2,store,key)
% Update results from the job ValueStore object.
result = store(key);

% Estimate pi with all the data stored in the ValueStore object.
keyset = keys(store); % Return all the keys of the ValueStore object. 
all_data = cell2mat(get(store,keyset)); % Convert to a structure array.
hits = [all_data.in_circle]; % Concatenate the result from each key.
pi_estimate = (sum(hits)*4)/(numel(hits)); 

% Update the plots with the new x and y values and the estimate of pi.
hold([ax1 ax2],'on');
plot(ax1,result.x,result.y,'.',Color=result.point_color);
plot(ax2,numel(hits),pi_estimate,".-k");
title(ax2,"Current Estimate of $\pi$",num2str(pi),Interpreter="latex");
hold([ax1 ax2],'off');
drawnow nocallbacks;
end

简单蒙特卡罗面积方法

给定一个半径为 r 的圆，它内接于一个边长为 2r 的正方形，则圆的面积与正方形的面积之比为 π。该图很能说明问题。

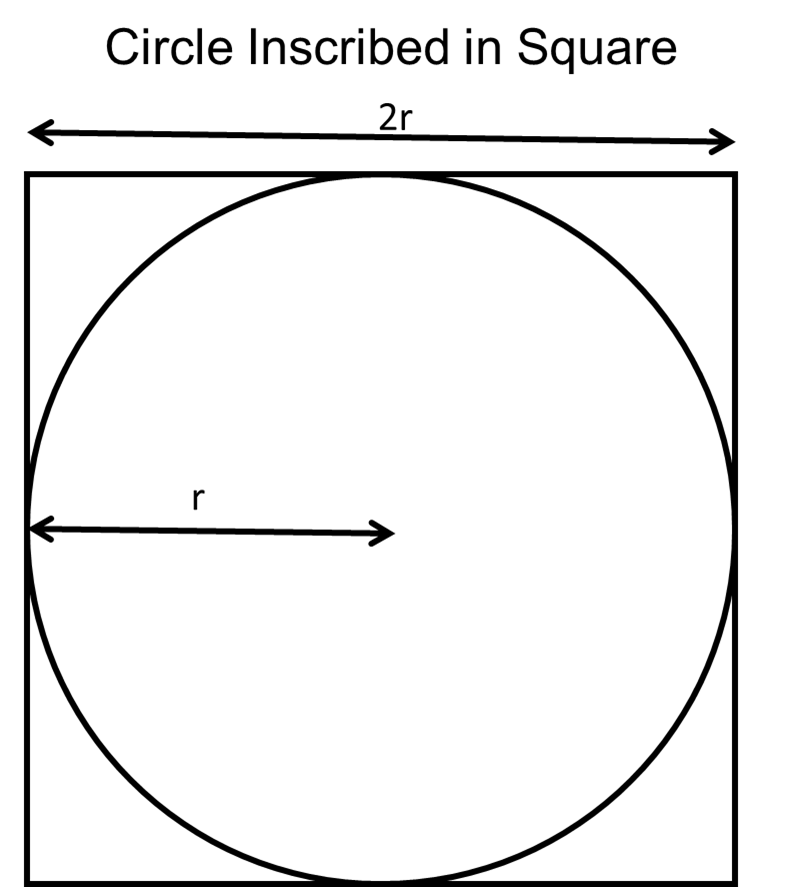
您可以通过圆面积除以正方形面积的比率来推导出 π：

$\frac{area of circle}{area of square} =$

$\frac{π r^{2}}{{(2 r)}^{2}} = \frac{π}{4}$

为了在不直接使用 π 的情况下估计圆的面积，请在正方形内随机生成二维（2-D）点的均匀样本，并计算圆内有多少个点。在圆中找到一个点的概率是圆的面积除以正方形的面积之比。

为了判断某个点是否在圆内，随机生成两个值，分别为该点的 $x$ 和 $y$ 坐标，并计算该点与圆原点之间的距离。从原点到生成点的距离 $d$ 由以下方程给出：

$d = \sqrt{x^{2} + y^{2}}$

如果 $d$ 小于圆的半径 $r$ ，则该点位于圆内。生成大量点样本并计算圆内有多少个点。使用此数据来获取圆内的点与生成的总点数的比例。这个比率相当于圆的面积与正方形的面积之比。然后您可以使用以下公式估算 π：

$\frac{points in circle}{total number of points} \approx \frac{π}{4}$

$π \approx 4 \times \frac{points in circle}{total number of points}$

另请参阅

batch | ValueStore | createCommunicatingJob