使用并行计算优化大数据集进行分析
此示例展示如何使用并行计算优化数据预处理以进行分析。
通过优化时间序列数据的组织和存储，您可以简化和加速任何下游应用程序，如预测性维护、数字孪生、基于信号的人工智能和车队分析。
在此示例中，您将大量原始数据转换为可供将来分析的状态，并使用并行工作进程将其保存到 Parquet 文件中。Parquet 文件提供高效的数据访问，因为它们高效地存储面向列的异构数据，允许您有条件地按行过滤文件并仅加载所需的数据。接下来，您可以使用内存外数据来训练一个简单的 AI 模型。
如果您有数据存储在集群上，则可以使用此代码进行类似的数据优化，而无需下载数据。要查看对存储在云中的数据进行分析的示例，请参阅 在云端处理大数据。
启动一个并行进程工作进程。
pool = parpool("Processes");Starting parallel pool (parpool) using the 'Processes' profile ... 15-Jan-2024 12:03:49: Job Running. Waiting for parallel pool workers to connect ... Connected to parallel pool with 6 workers.
下载航班数据
此示例使用 NASA [1] 提供的样本飞机传感器数据。
如果您想自己尝试这些数据预处理技术，则必须下载飞机传感器数据。NASA 提供了大约 180,000 次航班的数据，每次航班对应一个 MAT 文件。有关详细信息，请参阅示例飞行数据。
此代码在您当前文件夹中创建一个文件夹并下载飞机尾号 652 第一年的数据，该数据占用大约 1.6 GB 的磁盘空间。下载数据可能需要几分钟。为了确认您想要下载数据，请在运行示例之前从下拉列表中选择“true"”。
downloadIfTrue =false; if downloadIfTrue downloadNASAFlightData(pwd,"small"); dataRoot = fullfile(pwd,"data"); else disp("Confirm and download flight data to proceed."); return end
Organizing MAT files into folders... MAT files organized into folders.
downloadNASAFlightData 函数下载尾部 652 的文件并将其组织到每个月的子文件夹中。
将数据转换为嵌套表
检查飞行数据样本。每个 MAT 文件包含 186 个结构数组，每个结构数组代表一个传感器。每个结构数组将与传感器相关的元数据与嵌套数组中的传感器读数一起存储。此外，文件名还包含重要的元数据，例如航班 ID、尾号和开始时间。
sampleData = matfile(fullfile(dataRoot,"mat","Tail_652\200101\652200101092009.mat")); sampleData.ABRK
ans = struct with fields:
data: [1972×1 double]
Rate: 1
Units: 'DEG'
Description: 'AIRBRAKE POSITION'
Alpha: 'ABRK'
将每个传感器的数据存储为单独的结构变量或将元数据嵌入文件名中效率不高。相反，您可以将数据组织成嵌套模式。通过这种方法，您可以轻松搜索元数据，并通过嵌套传感器值来减少表中的行数。使用 struct2table 函数来组织样本结构数组。
struct2table(sampleData.ABRK,AsArray=true)
ans=1×5 table
data Rate Units Description Alpha
_______________ ____ _______ _____________________ ________
{1972×1 double} 1 {'DEG'} {'AIRBRAKE POSITION'} {'ABRK'}
returnNestedTable 辅助函数将 struct2table 函数应用于示例 MAT 文件中的每个传感器数据并垂直连接结果。
head(returnNestedTable(fullfile(dataRoot,"mat","Tail_652\200101\652200101092009.mat")))
StartTime TailNumber FlightId Rate Alpha Description Units data
_______________________ __________ _______________ ____ ________ ____________________________ ___________ _______________
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'1107'} {'SYNC WORD FOR SUBFRAME 1'} {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'2670'} {'SYNC WORD FOR SUBFRAME 2'} {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'5107'} {'SYNC WORD FOR SUBFRAME 3'} {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'6670'} {'SYNC WORD FOR SUBFRAME 4'} {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'A/T' } {'THRUST AUTOMATIC ON' } {0×0 char } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'ABRK'} {'AIRBRAKE POSITION' } {'DEG' } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'ACID'} {'AIRCRAFT NUMBER' } {0×0 char } { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'ACMT'} {'ACMS TIMING USED T1HZ' } {0×0 char } {1972×1 double}
创建文件数据存储
数据存储是用于存储因内存太大而无法容纳的数据的存储库。您可以将存储在多个文件中的数据作为单个实体进行读取和进程。要了解更多信息，请参阅 数据存储快速入门。
使用 652 号尾部第一年的数据文件创建一个 FileDatastore 对象。您必须使用 returnNestedTable 自定义读取函数来读取 MAT 文件中的数据。
dsFlight = fileDatastore(fullfile(dataRoot,"mat","Tail_652"), ... ReadFcn=@returnNestedTable,IncludeSubfolders=true, ... FileExtensions=".mat",UniformRead=true);
预览数据存储。该表的输出与在没有数据存储的情况下调用 returnNestedTable 读取函数时的表输出相同。
preview(dsFlight)
ans=186×8 table
StartTime TailNumber FlightId Rate Alpha Description Units data
_______________________ __________ _______________ ____ _________ _____________________________ ___________ _______________
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'1107' } {'SYNC WORD FOR SUBFRAME 1' } {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'2670' } {'SYNC WORD FOR SUBFRAME 2' } {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'5107' } {'SYNC WORD FOR SUBFRAME 3' } {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'6670' } {'SYNC WORD FOR SUBFRAME 4' } {'<units>'} { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'A/T' } {'THRUST AUTOMATIC ON' } {0×0 char } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'ABRK' } {'AIRBRAKE POSITION' } {'DEG' } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 {'ACID' } {'AIRCRAFT NUMBER' } {0×0 char } { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'ACMT' } {'ACMS TIMING USED T1HZ' } {0×0 char } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'AIL.1'} {'AILERON POSITION LH' } {'DEG' } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'AIL.2'} {'AILERON POSITION RH' } {'DEG' } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 4 {'ALT' } {'PRESSURE ALTITUDE LSP' } {'FEET' } {7888×1 double}
2001-01-09 20:09:00.000 652 652200101092009 4 {'ALTR' } {'ALTITUDE RATE' } {'FT/MIN' } {7888×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 {'ALTS' } {'SELECTED ALTITUDE LSP' } {'FEET' } {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 4 {'AOA1' } {'ANGLE OF ATTACK 1' } {'DEG' } {7888×1 double}
2001-01-09 20:09:00.000 652 652200101092009 4 {'AOA2' } {'ANGLE OF ATTACK 2' } {'DEG' } {7888×1 double}
2001-01-09 20:09:00.000 652 652200101092009 4 {'AOAC' } {'CORRECTED ANGLE OF ATTACK'} {'DEG' } {7888×1 double}
⋮
清理数据
接下来，清理数据以供将来的分析。使用 transform 函数执行一些表操作并更改表变量的数据类型。数据存储区会推迟执行转换，直到您从中读取或写入为止。
将 Alpha 和 data 变量重命名为 SensorName 和 Data。
tdsFlight1 = transform(dsFlight,@(t) renamevars(t,["Rate","Alpha","data"], ... ["SampleRate","SensorName","Data"]));
将所有字符向量单元格数组变量转换为字符串数组。为了稍后对数据进行分类，将 Units 变量转换为 categorical 数组，将 SampleRate 变量转换为单个数组。预览转换后的数据存储的结果样本。
tdsFlight2 = transform(tdsFlight1,@(t) convertvars(t,vartype("cellstr"),"string")); tdsFlight3 = transform(tdsFlight2,@(t) convertvars(t,"Units","categorical")); tdsFlight4 = transform(tdsFlight3,@(t) convertvars(t,"SampleRate","single")); preview(tdsFlight4)
ans=8×8 table
StartTime TailNumber FlightId SampleRate SensorName Description Units Data
_______________________ __________ _______________ __________ __________ __________________________ ___________ _______________
2001-01-09 20:09:00.000 652 652200101092009 0.25 "1107" "SYNC WORD FOR SUBFRAME 1" <units> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "2670" "SYNC WORD FOR SUBFRAME 2" <units> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "5107" "SYNC WORD FOR SUBFRAME 3" <units> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "6670" "SYNC WORD FOR SUBFRAME 4" <units> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 "A/T" "THRUST AUTOMATIC ON" <undefined> {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 "ABRK" "AIRBRAKE POSITION" DEG {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "ACID" "AIRCRAFT NUMBER" <undefined> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 "ACMT" "ACMS TIMING USED T1HZ" <undefined> {1972×1 double}
对单位变量的缺失值进行标准化。MATLAB 使用 <undefined> 标记来标记分类值中的缺失数据，但 Unit 变量的某些行也显示 <units> 或 UNITS，您可以将其视为此数据集中的缺失数据。使用转换函数对其进行标准化，以便单位变量中的每个缺失值都使用统一的缺失标记。预览转换后的数据存储的结果样本。
tdsFlight5 = transform(tdsFlight4,@(t) standardizeMissing(t,["<units>","UNITS"], ... DataVariables="Units")); preview(tdsFlight5)
ans=8×8 table
StartTime TailNumber FlightId SampleRate SensorName Description Units Data
_______________________ __________ _______________ __________ __________ __________________________ ___________ _______________
2001-01-09 20:09:00.000 652 652200101092009 0.25 "1107" "SYNC WORD FOR SUBFRAME 1" <undefined> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "2670" "SYNC WORD FOR SUBFRAME 2" <undefined> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "5107" "SYNC WORD FOR SUBFRAME 3" <undefined> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "6670" "SYNC WORD FOR SUBFRAME 4" <undefined> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 "A/T" "THRUST AUTOMATIC ON" <undefined> {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 "ABRK" "AIRBRAKE POSITION" DEG {1972×1 double}
2001-01-09 20:09:00.000 652 652200101092009 0.25 "ACID" "AIRCRAFT NUMBER" <undefined> { 493×1 double}
2001-01-09 20:09:00.000 652 652200101092009 1 "ACMT" "ACMS TIMING USED T1HZ" <undefined> {1972×1 double}
并行写入 Parquet 文件
现在数据已优化并准备好进行未来的分析，请使用 writeall 函数将最终转换后的数据存储中的数据保存为 Parquet 文件。Parquet 文件格式支持列式异构数据的有效压缩、编码和提取。当您将 UseParallel 设置为 true 时，writeall 函数会自动使用开放并行池的工作进程来应用转换函数，并将转换后的数据存储的内容写入文件。
此代码为数据存储中的每个 MAT 文件创建一个 Parquet 文件，并将 Parquet 文件保存在 parquet_sample 文件夹中，保留原始 MAT 文件的文件夹结构。此进程将 2.6 GB 的数据写入磁盘。为了确认您想要保存数据，请在运行示例之前从下拉列表中选择 "true"。
saveIfTrue =false; if saveIfTrue outdir = fullfile(dataRoot,"parquet_sample"); if isfolder(outdir) rmdir(outdir,"s"); end writeall(tdsFlight5,outdir,FolderLayout="duplicate", ... OutputFormat="parquet",UseParallel=true) disp("Parquet files saved to the parquet_sample folder.") else disp("Confirm and save modified flight data to proceed.") end
Parquet files saved to the parquet_sample folder.
writeall 函数将 Parquet 文件保存到每个月的子文件夹中。
提取数据来训练神经网络
深度学习利用神经网络直接从数据中提取有用的模式和特征。要了解更多信息，请参阅 在 MATLAB 中进行深度学习 (Deep Learning Toolbox)。
现在数据已经干净且井然有序，您可以使用传感器数据的子集来训练神经网络。您可以使用时间序列传感器数据（例如高度压力、燃油流量、风扇速度、当前真实空速、风向和风速）预测飞机未来在巡航高度的真实空速。要训练神经网络来预测真实空速，可以使用长短期记忆 (LSTM) 网络。LSTM 网络在序列到序列预测方面表现出色，这使其成为时间序列数据的理想选择。它们识别数据序列中的模式并预测每个时间步骤的未来值。
对于此示例，使用每个航班的传感器时间序列作为训练数据序列。为了预测未来的真实空速，用未来一个时间步长偏移的真实空速值作为目标来训练网络。这种方法意味着在输入序列的每个时间步，LSTM 都会预测下一个时间步的真实空速值。
提取数据
首先提取 2001 年 1 月至 4 月以及 2001 年 6 月的航班数据。2001 年 5 月以来的数据不可用。
创建一个 parquetDatastore 并使用 SelectedVariableNames 属性仅导入 StartTime、SampleRate、SensorName 和 Data 变量。每个文件都包含单次航班的所有数据，因此将 ReadSize 属性设置为 file 以一次读取和进程一个文件。ReadSize 属性还决定了软件在将数据发送到每个并行工作进程之前如何对其进行分区。
pdsFlight = parquetDatastore(fullfile(dataRoot,"parquet_sample","Tail_652"), ... IncludeSubfolders=true,ReadSize="file", ... SelectedVariableNames=["StartTime","SampleRate","SensorName","Data"]);
要导入 2001 年 1 月至 4 月以及 2001 年 6 月的数据，请使用 ParquetDatastore 对象创建行过滤器。然后，使用行过滤器选择 StartTime 值大于或等于 2001 年 1 月且 StartTime 值小于 2001 年 7 月的行。预览过滤后的数据存储。
rf = rowfilter(pdsFlight); pdsFlight.RowFilter = rf.StartTime >= datetime("2001-01-01")... & rf.StartTime < datetime("2001-07-01"); preview(pdsFlight)
ans=8×4 table
StartTime SampleRate SensorName Data
____________________ __________ __________ _______________
09-Jan-2001 20:09:00 0.25 "1107" { 493×1 double}
09-Jan-2001 20:09:00 0.25 "2670" { 493×1 double}
09-Jan-2001 20:09:00 0.25 "5107" { 493×1 double}
09-Jan-2001 20:09:00 0.25 "6670" { 493×1 double}
09-Jan-2001 20:09:00 1 "A/T" {1972×1 double}
09-Jan-2001 20:09:00 1 "ABRK" {1972×1 double}
09-Jan-2001 20:09:00 0.25 "ACID" { 493×1 double}
09-Jan-2001 20:09:00 1 "ACMT" {1972×1 double}
提取每次飞行的巡航阶段。使用 nested2wide 辅助函数将嵌套的传感器数据转换为单独的变量，并提取高度压力（ALT）、燃油流量（FF.1）、风扇速度（N1.1 和 N2.1）、真空速（(TAS）、风向（WD）、风速（WS）和车轮重量（WOW）变量。为了解决不同的采样率，nested2wide 函数会用前一个非缺失值填充任何缺失值。
extractCruise 辅助函数识别航班的巡航阶段，并仅返回包含巡航部分的部分作为时间表。如果该函数未检测到巡航阶段，或者检测到多个单独的巡航，则该函数返回一个空的时间表。
使用一次转换将嵌套的传感器数据转换为变量，从包含巡航部分的文件中识别并返回时间表。
tpdsFlight = transform(pdsFlight,@(t) extractCruise ... (nested2wide(t,["ALT","FF.1","N1.1","N2.1","TAS","WD","WS","WOW"])));
并非所有文件都会返回数据，因为只有大约 60% 的航班包含巡航阶段。其余都是短途飞行或从未离开地面的飞行。要找到包含巡航部分的文件的索引，请使用转换来识别 tpdsFlight 数据存储中未返回空表的文件，并使用 readall 函数并行收集索引。要返回仅包含具有巡航部分的文件的数据存储，请将 subset 函数与 tpdsFlight 数据存储和与这些文件对应的索引一起使用。
dsHasCruisePhase = transform(tpdsFlight,@(t) ~isempty(t)); indices = readall(dsHasCruisePhase,UseParallel=true); tpdsFlightCruise = subset(tpdsFlight,indices); preview(tpdsFlightCruise)
ans=3043×8 timetable
timestamp ALT FF.1 N1.1 N2.1 TAS WD WOW WS
_______________________ _____ ____ ______ ______ ______ ______ ___ ______
2001-01-13 08:20:41.500 21757 1656 93.906 92.938 393.38 65.391 1 11.953
2001-01-13 08:20:41.750 21760 1656 93.906 92.938 393.38 66.094 1 11.953
2001-01-13 08:20:42.000 21763 1656 93.906 92.938 393.44 66.094 1 12.949
2001-01-13 08:20:42.250 21766 1656 93.906 92.938 393.56 66.797 1 12.949
2001-01-13 08:20:42.500 21768 1656 93.906 92.938 393.06 68.203 1 12.949
2001-01-13 08:20:42.750 21771 1656 93.906 92.938 393.06 69.609 1 12.949
2001-01-13 08:20:43.000 21775 1656 93.906 92.938 393.06 68.906 1 12.949
2001-01-13 08:20:43.250 21779 1656 93.906 92.938 393.06 68.203 1 11.953
2001-01-13 08:20:43.500 21781 1656 93.906 92.906 393 68.203 1 11.953
2001-01-13 08:20:43.750 21786 1656 93.875 92.906 393.12 67.5 1 11.953
2001-01-13 08:20:44.000 21788 1656 93.875 92.938 393.12 67.5 1 11.953
2001-01-13 08:20:44.250 21790 1656 93.906 92.938 393.06 67.5 1 11.953
2001-01-13 08:20:44.500 21795 1656 93.906 92.938 393.19 67.5 1 11.953
2001-01-13 08:20:44.750 21799 1656 93.906 93 393.62 66.797 1 11.953
2001-01-13 08:20:45.000 21800 1656 93.938 93 393.38 66.797 1 11.953
2001-01-13 08:20:45.250 21804 1656 93.906 92.938 393.12 68.203 1 11.953
⋮
准备训练数据
使用 trainingPartitions 辅助函数将 tpdsFlightCruise 数据存储随机划分为包含 70% 文件的训练集、包含 15% 文件的验证集和包含剩余 15% 文件的测试集。
numCruiseFlights = sum(indices); [indexTrain,indexValidation,indexTest] = trainingPartitions(numCruiseFlights,[0.70 0.15 0.15]);
对 tpdsFlightCruise 数据存储进行子集化以获取 pdsTrain 训练数据存储。
pdsTrain = subset(tpdsFlightCruise,indexTrain);
为了更好地拟合并防止训练发散，您必须规范化训练、验证和测试数据。在此示例中，您使用训练数据存储中所有数据的最小值和最大值将训练、验证和测试数据中的传感器变量重新缩放到范围 [0,1]。
为了轻松计算所有训练数据的最小值和最大值，请使用来自 pdsTrain 数据存储的数据创建一个 tall 时间表。从 tall 时间表中提取训练所需的变量，并计算最小值和最大值。当您使用 gather 函数将结果收集到内存中时，MATLAB 会自动在开放并行池的工作进程上并行执行计算。
testDataTT = tall(pdsTrain);
tallTrainDs = testDataTT{:,["ALT","FF.1","N1.1","N2.1","TAS","WD","WS"]};
[stats.min,stats.max] = gather(min(tallTrainDs),max(tallTrainDs));Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 27 sec Evaluation completed in 28 sec
创建一个转换后的数据存储，删除 timestamp 和 WOW 变量，并使用 prepareMLData 辅助函数返回可供训练的数据。
对于单个输入层，神经网络期望数据存储输出一个表，该表的行对应于训练数据中的序列数，以及两个分别指定预测变量和目标的变量。每个预测因子或目标序列必须表示为 t-by-c 数值数组，其中 t 和 c 分别表示每个序列中的时间步长和特征的数量。在此示例中，每个文件都是一个训练数据序列，因此您必须转换训练数据存储以输出一个表，该表包含两个变量（分别表示预测变量和目标数据），每个文件一行。
prepareMLData 辅助函数首先根据 stats 结构中的最小值和最大值对数据进行规范化。为了为每个文件创建预测数据，prepareMLData 辅助函数将序列中的所有七个传感器变量组合成一个 t-by-7数组，不包括最后时间步的传感器数据。此外，该函数通过删除第一个时间步长的数据并将剩余时间步长的值组合成单个 t-by-1数组来创建目标真实空速值。
tpdsTrain = transform(pdsTrain,@(t) prepareMLData(t,"TAS","training",stats));
预览转换后的训练数据存储。
preview(tpdsTrain)
ans=1×2 table
Predictors Targets
_______________ _______________
{1379×7 double} {1379×1 double}
准备验证和测试数据
从 tpdsFlightCruise 数据存储中分区 15% 的数据以用作验证数据 pdsValid 数据存储。
pdsValid = subset(tpdsFlightCruise,indexValidation);
在转换中使用 prepareMLData 辅助函数来删除 timestamp 和 WOW 变量并返回可供训练的验证数据。prepareMLData 函数将验证数据转换为与训练数据相同的格式。
tpdsValid = transform(pdsValid,@(t) prepareMLData(t,"TAS","training",stats)); preview(tpdsValid)
ans=1×2 table
Predictors Targets
_______________ _______________
{2187×7 double} {2187×1 double}
从 tpdsFlightCruise 数据存储中分区 15% 的数据以用作测试数据存储。
tpdsTest = subset(tpdsFlightCruise,indexTest);
使用 prepareMLData 辅助函数删除 timestamp 和 WOW 变量并返回所有七个传感器变量（不包括序列中最后时间步骤的传感器数据），组合成一个数组。
tpdsTestPredictors = transform(tpdsTest,@(t) prepareMLData(t,"TAS","testPredictors",stats)); preview(tpdsTestPredictors)
使用 prepareMLData 辅助函数删除 timestamp 和 WOW 变量并返回按一个时间步长偏移的测试目标真实空速值。prepareMLData 函数没有对测试目标数据进行规范化。
tpdsTestTargets = transform(tpdsTest,@(t) prepareMLData(t,"TAS","testTargets",stats)); preview(tpdsTestTargets)
训练和测试神经网络
定义网络架构并训练网络
要创建 LSTM 网络，请指定以下层序列：
序列输入层的大小与输入特征的数量相匹配，在此示例中为七个（ALT、FF.1、N1.1、N2.1、TAS、WD 和 WS）。
具有 64 个隐藏单元的 LSTM 层，可输出完整序列。
全连接层的输出大小设置为 136，对应 136 个隐藏神经元。
丢失概率为 0.60211 的丢失层。
全连接层，其输出大小与输出数量匹配，在此示例中为 1（TAS）。
numFeatures = 7; numHiddenUnits = 64; numResponses = 1; layers = [ ... sequenceInputLayer(numFeatures,Normalization="none") lstmLayer(numHiddenUnits,OutputMode="sequence") fullyConnectedLayer(136) dropoutLayer(0.60211) fullyConnectedLayer(numResponses)];
定义培训选项。
使用“
ADAM”优化器进行训练，训练周期为 20 个时期，小批量大小为 1。将学习率指定为 0.01，将梯度阈值指定为 1。
为了在训练期间定期验证网络，请将验证数据存储指定为
tpdsValid并将验证频率设置为 30。将
ExecutionEnvironment设置为"parallel-auto"以使用并行池进行训练。如果当前没有并行池，软件将使用默认集群配置文件启动一个并行池。如果池可以访问 GPU，那么只有具有唯一 GPU 的工作进程才会执行训练计算，而多余的工作进程则会闲置。监控均方误差 (MSE) 指标并在图中显示训练进度。
maxEpochs = 20; miniBatchSize = 1; options = trainingOptions("adam", ... MaxEpochs=maxEpochs, ... MiniBatchSize=miniBatchSize, ... InitialLearnRate=0.01, ... GradientThreshold=1, ... ValidationData=tpdsValid, ... ValidationFrequency=30, ... ExecutionEnvironment="parallel-auto", ... Metrics="rmse", ... Plots="training-progress", ... Verbose=0);
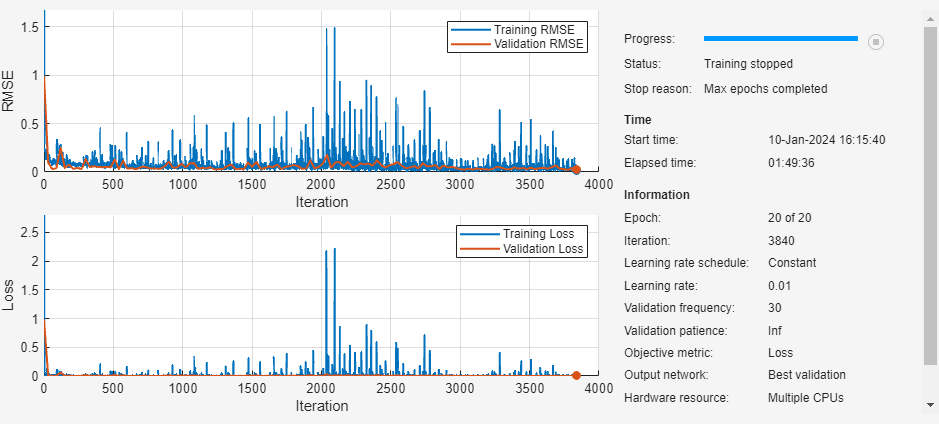
训练神经网络。因为这是一个回归任务，所以使用均方误差损失。
net = trainnet(tpdsTrain,layers,"mse",options);
测试网络
您可以使用训练过的神经网络来预测测试数据存储中每个飞行序列的真实空速。预测完成后，将归一化的预测值转换为真实值。
yPred = minibatchpredict(net,tpdsTestPredictors,MiniBatchSize=1,UniformOutput=false); minTAS = stats.min(5); maxTAS = stats.max(5); predictedTrueAirspeeds = cellfun(@(x) (maxTAS-minTAS)*(x+minTAS),yPred,UniformOutput=false);
提取目标真空速值进行比较。将 UseParallel 设置为 true 以使用开放并行池的工作进程。
targetY = readall(tpdsTestTargets,UseParallel=true);
targetTrueAirspeeds = targetY.("Test Targets");在图中比较目标和预测的真实空速。
idx = randperm(length(predictedTrueAirspeeds),4); figure tiledlayout(2,2) for i = 1:numel(idx) nexttile plot(targetTrueAirspeeds{idx(i)},"--") hold on plot(predictedTrueAirspeeds{idx(i)},".-") hold off title("Test Flight " + idx(i)) xlabel("Time Step") ylabel("TAS (knots)") legend(["Test Data","Predicted"],Location="best") end
计算最大绝对误差的平均值、最大相对误差（占目标值的一部分）以及目标和预测真实空速值之间的平均 RMSE。
absErrors = cellfun(@(x1,x2) max(abs(x1-x2)),targetTrueAirspeeds,predictedTrueAirspeeds);
maxRelativeError = cellfun(@(x1,x2) max((abs(x1-x2)./x1)),targetTrueAirspeeds,predictedTrueAirspeeds);
rootMeanSE = cellfun(@(x1,x2) rmse(x1,x2),targetTrueAirspeeds,predictedTrueAirspeeds);
meanAbsErrors = mean(absErrors);
fprintf("Mean maximum absolute error = %5.4f knots",meanAbsErrors)Mean maximum absolute error = 79.2402 knots
meanRMSE = mean(rootMeanSE);
fprintf("Mean RMSE = %5.4f knots",meanRMSE)Mean RMSE = 11.3948 knots
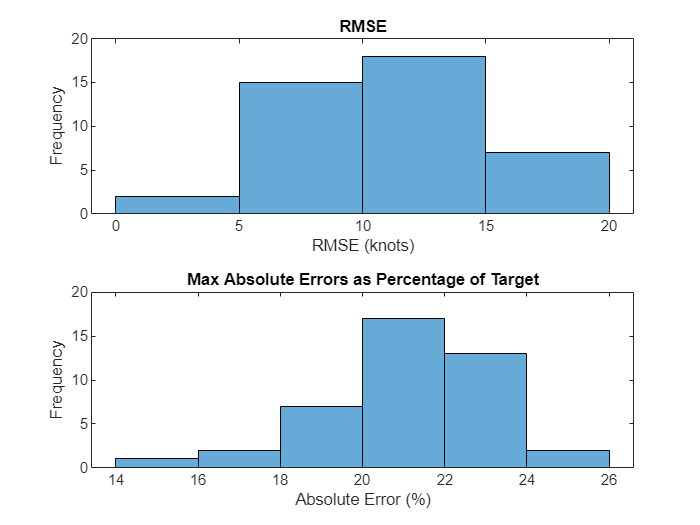
绘制试飞数据的最大绝对误差。
figure nexttile histogram(rootMeanSE) xlabel("RMSE (knots)") ylabel("Frequency") title("RMSE") nexttile histogram(maxRelativeError*100) xlabel("Absolute Error (%)") ylabel("Frequency") title("Max Absolute Errors as Percentage of Target")
清理
删除飞行数据文件并删除并行池。
rmdir(dataRoot,"s");
delete(pool);参考
[1] “Flight Data For Tail 652 | NASA Open Data Portal.”Accessed October 6, 2023. https://data.nasa.gov/dataset/Flight-Data-For-Tail-652/fxpu-g6k3.
另请参阅
parfor | fileDatastore | transform | writeall
相关主题
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)