Main Content

solvepdeeig

Solve PDE eigenvalue problem specified in a PDEModel

collapse all in page

Syntax

result = solvepdeeig(model,evr)

Description

example

result = solvepdeeig(model,evr) solves the PDE eigenvalue problem in model for eigenvalues in the range evr. If the range does not contain any eigenvalues, solvepdeeig returns an EigenResults object with the empty EigenVectors, EigenValues, and Mesh properties.

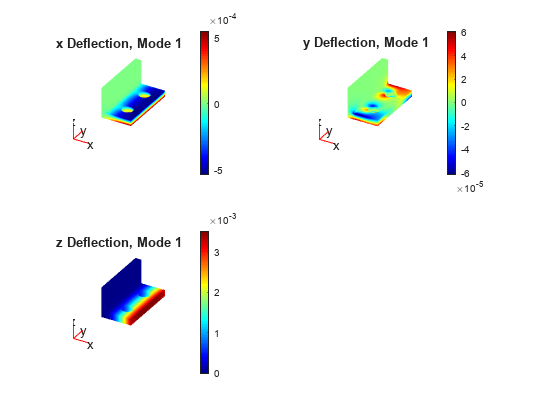
Examples

collapse all

Open Live Script

Solve for several vibrational modes of the BracketTwoHoles geometry.

The equations of elasticity have three components. Therefore, create a PDE model that has three components. Import and view the BracketTwoHoles geometry.

model = createpde(3);
importGeometry(model,"BracketTwoHoles.stl");
pdegplot(model,"FaceLabels","on","FaceAlpha",0.4)

Figure contains an axes object. The axes object contains 3 objects of type quiver, patch, line.

Set F1, the rear face, to have zero deflection.

applyBoundaryCondition(model,"dirichlet","Face",1,"u",[0;0;0]);

Set the model coefficients to represent a steel bracket. For details, see Linear Elasticity Equations. When specifying the f-coefficient, assume that all body forces are zero.

E = 200e9; % elastic modulus of steel in Pascals
nu = 0.3; % Poisson's ratio
specifyCoefficients(model,"m",0,...
                          "d",1,...
                          "c",elasticityC3D(E,nu),...
                          "a",0,...
                          "f",[0;0;0]);

Find the eigenvalues up to 1e7.

evr = [-Inf,1e7];

Mesh the model and solve the eigenvalue problem.

generateMesh(model);
results = solvepdeeig(model,evr);
              Basis= 10,  Time=   1.73,  New conv eig=  0
              Basis= 11,  Time=   1.76,  New conv eig=  0
              Basis= 12,  Time=   1.77,  New conv eig=  0
              Basis= 13,  Time=   1.79,  New conv eig=  0
              Basis= 14,  Time=   1.82,  New conv eig=  1
              Basis= 15,  Time=   1.83,  New conv eig=  2
              Basis= 16,  Time=   1.85,  New conv eig=  2
              Basis= 17,  Time=   1.87,  New conv eig=  2
              Basis= 18,  Time=   1.90,  New conv eig=  2
              Basis= 19,  Time=   1.93,  New conv eig=  5
End of sweep: Basis= 19,  Time=   1.93,  New conv eig=  5
              Basis= 15,  Time=   2.12,  New conv eig=  0
End of sweep: Basis= 15,  Time=   2.14,  New conv eig=  0

How many results did solvepdeeig return?

length(results.Eigenvalues)
ans = 3

Plot the solution on the geometry boundary for the lowest eigenvalue.

V = results.Eigenvectors;
subplot(2,2,1)
pdeplot3D(model,"ColorMapData",V(:,1,1))
title("x Deflection, Mode 1")
subplot(2,2,2)
pdeplot3D(model,"ColorMapData",V(:,2,1))
title("y Deflection, Mode 1")
subplot(2,2,3)
pdeplot3D(model,"ColorMapData",V(:,3,1))
title("z Deflection, Mode 1")

Plot the solution for the highest eigenvalue.

figure
subplot(2,2,1)
pdeplot3D(model,"ColorMapData",V(:,1,3))
title("x Deflection, Mode 3")
subplot(2,2,2)
pdeplot3D(model,"ColorMapData",V(:,2,3))
title("y Deflection, Mode 3")
subplot(2,2,3)
pdeplot3D(model,"ColorMapData",V(:,3,3))
title("z Deflection, Mode 3")

Input Arguments

collapse all

PDE model, specified as a PDEModel object. The model contains the geometry, mesh, and problem coefficients.

Example: model = createpde(1)

Eigenvalue range, specified as a two-element real vector. evr(1) specifies the lower limit of the range of the real part of the eigenvalues, and may be -Inf. evr(2) specifies the upper limit of the range, and must be finite.

Example: [-Inf;100]

Data Types: double

Output Arguments

collapse all

Eigenvalue results, returned as an EigenResults object. If the range env does not contain any eigenvalues, the returned EigenResults object has the empty EigenVectors, EigenValues, and Mesh properties.

Tips

  • The equation coefficients cannot depend on the solution u or its gradient.

Version History

Introduced in R2016a

See Also

| | |

Topics