pdeplot3D

Plot solution or surface mesh for 3-D problem

collapse all in page

Syntax

pdeplot3D(results.Mesh,ColorMapData=results.VonMisesStress,Deformation=results.Displacement)

pdeplot3D(results.Mesh,ColorMapData=results.Temperature)

pdeplot3D(results.Mesh,ColorMapData=results.ElectricPotential)

pdeplot3D(results.Mesh,ColorMapData=results.NodalSolution)

pdeplot3D(mesh)

pdeplot3D(nodes,elements)

pdeplot3D(model)

pdeplot3D(___,Name,Value)

h = pdeplot3D(___)

Description

pdeplot3D(results.Mesh,ColorMapData=results.VonMisesStress,Deformation=results.Displacement) plots the von Mises stress and shows the deformed shape for a 3-D structural analysis problem.

example

pdeplot3D(results.Mesh,ColorMapData=results.Temperature) plots the temperature at nodal locations for a 3-D thermal analysis problem.

example

pdeplot3D(results.Mesh,ColorMapData=results.ElectricPotential) plots the electric potential at nodal locations for a 3-D electrostatic analysis problem.

example

pdeplot3D(results.Mesh,ColorMapData=results.NodalSolution) plots the solution at nodal locations.

example

pdeplot3D(mesh) plots the mesh.

example

pdeplot3D(nodes,elements) plots the mesh defined by nodes and elements.

example

pdeplot3D(model) plots the surface mesh specified in model. This syntax does not work with an femodel object.

pdeplot3D(___,Name,Value) plots the surface mesh, the data at nodal locations, or both the mesh and data, depending on the Name,Value pair arguments. Use any arguments from the previous syntaxes.

example

h = pdeplot3D(___) returns a handle to a plot, using any of the previous syntaxes.

Examples

collapse all

Deformed Shape for Cantilever Beam Problem

Open Live Script

Create an femodel object for static structural analysis and include the geometry of a beam.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry="SquareBeam.stl");

Plot the geometry.

pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.5)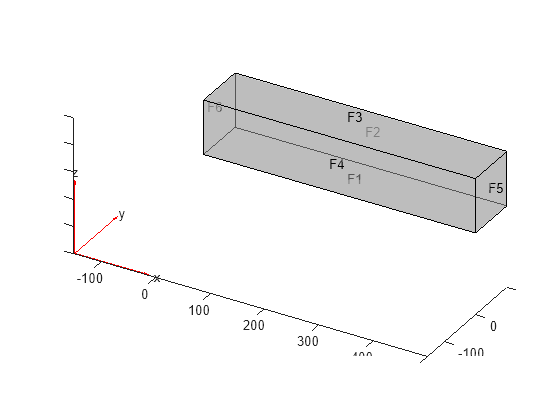

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Specify Young's modulus and Poisson's ratio.

model.MaterialProperties = ...
    materialProperties(PoissonsRatio=0.3, ...
                       YoungsModulus=210E3);

Specify that face 6 is a fixed boundary.

model.FaceBC(6) = faceBC(Constraint="fixed");

Specify the surface traction for face 5.

model.FaceLoad(5) = faceLoad(SurfaceTraction=[0;0;-2]);

Generate a mesh and solve the problem.

model = generateMesh(model);
R = solve(model);

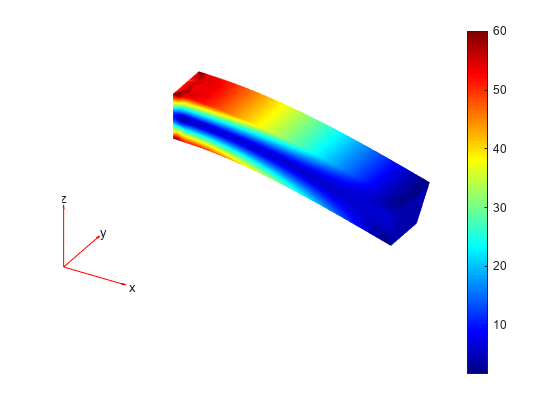
Plot the deformed shape with the von Mises stress using the default scale factor. By default, pdeplot3D internally determines the scale factor based on the dimensions of the geometry and the magnitude of deformation.

figure    
pdeplot3D(R.Mesh, ...
          ColorMapData=R.VonMisesStress, ...
          Deformation=R.Displacement)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

Plot the same results with the scale factor 500.

figure
pdeplot3D(R.Mesh, ...
          ColorMapData=R.VonMisesStress, ...
          Deformation=R.Displacement, ...
          DeformationScaleFactor=500)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

Plot the same results without scaling.

figure
pdeplot3D(R.Mesh, ...
          ColorMapData=R.VonMisesStress)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

von Mises Stress for 3-D Structural Dynamic Problem

Open Live Script

Evaluate the von Mises stress in a beam under a harmonic excitation.

Create and plot a beam geometry.

gm = multicuboid(0.06,0.005,0.01);
pdegplot(gm,FaceLabels="on",FaceAlpha=0.5)
view(50,20)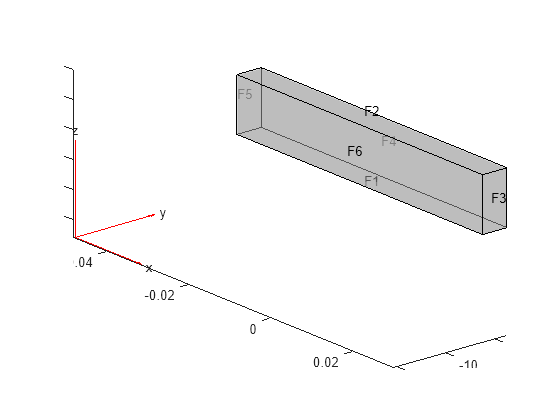

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Create an femodel for transient structural analysis and include the geometry.

model = femodel(AnalysisType="structuralTransient", ...
                Geometry=gm);

Specify Young's modulus, Poisson's ratio, and the mass density of the material.

model.MaterialProperties = ...
    materialProperties(YoungsModulus=210E9, ...
                       PoissonsRatio=0.3, ...
                       MassDensity=7800);

Fix one end of the beam.

model.FaceBC(5) = faceBC(Constraint="fixed");

Apply a sinusoidal displacement along the y-direction on the end opposite the fixed end of the beam.

yDisplacementFunc = ...
@(location,state) ones(size(location.y))*1E-4*sin(50*state.time);
model.FaceBC(3) = faceBC(YDisplacement=yDisplacementFunc);

Generate a mesh.

model = generateMesh(model,Hmax=0.01);

Specify the zero initial displacement and velocity.

model.CellIC = cellIC(Displacement=[0;0;0],Velocity=[0;0;0]);

Solve the model.

tlist = 0:0.002:0.2;
R = solve(model,tlist);

Evaluate the von Mises stress in the beam.

vmStress = evaluateVonMisesStress(R);

Plot the von Mises stress for the last time-step.

figure
pdeplot3D(R.Mesh,ColorMapData = vmStress(:,end))
title("von Mises Stress in the Beam for the Last Time-Step")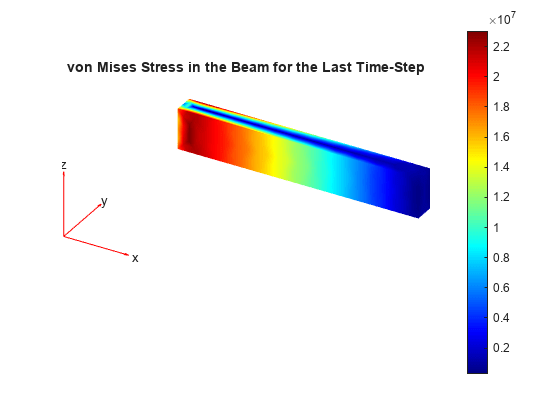

Figure contains an axes object. The hidden axes object with title von Mises Stress in the Beam for the Last Time-Step contains 5 objects of type patch, quiver, text.

Solve Steady-State Thermal Problem

Open Live Script

Solve a 3-D steady-state thermal problem.

Create an femodel object for a steady-state thermal problem and include a geometry representing a block.

model = femodel(AnalysisType="thermalSteady", ...
                Geometry="Block.stl");

Plot the block geometry.

pdegplot(model.Geometry, ...
         FaceLabels="on", ...
         FaceAlpha=0.5)
axis equal

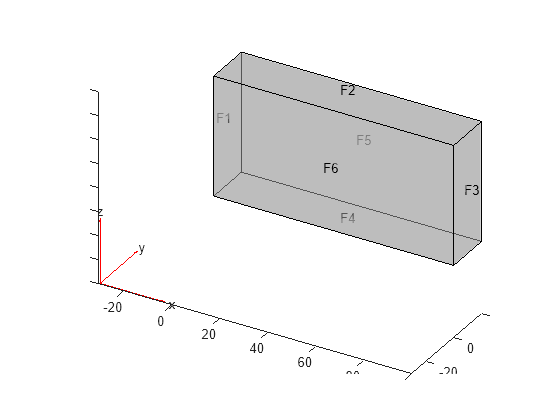
Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Assign material properties.

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=80);

Apply a constant temperature of 100 °C to the left side of the block (face 1) and a constant temperature of 300 °C to the right side of the block (face 3). All other faces are insulated by default.

model.FaceBC(1) = faceBC(Temperature=100);
model.FaceBC(3) = faceBC(Temperature=300);

Mesh the geometry and solve the problem.

model = generateMesh(model);
thermalresults = solve(model)

thermalresults = 
  SteadyStateThermalResults with properties:

    Temperature: [12822x1 double]
     XGradients: [12822x1 double]
     YGradients: [12822x1 double]
     ZGradients: [12822x1 double]
           Mesh: [1x1 FEMesh]

The solver finds the temperatures and temperature gradients at the nodal locations. To access these values, use thermalresults.Temperature, thermalresults.XGradients, and so on. For example, plot temperatures at the nodal locations.

pdeplot3D(thermalresults.Mesh,ColorMapData=thermalresults.Temperature)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

Heat Flux for 3-D Steady-State Thermal Problem

Open Live Script

For a 3-D steady-state thermal problem, evaluate heat flux at the nodal locations and at the points specified by x, y, and z coordinates.

Create an femodel object for steady-state thermal analysis and include a block geometry in the model.

model = femodel(AnalysisType="thermalSteady", ...
                Geometry="Block.stl");

Plot the geometry.

pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.5)
title("Copper block, cm")
axis equal

Figure contains an axes object. The axes object with title Copper block, cm contains 6 objects of type quiver, text, patch, line.

Assuming that this is a copper block, the thermal conductivity of the block is approximately $4 W / (c m K)$ .

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=4);

Apply a constant temperature of 373 K to the left side of the block (face 1) and a constant temperature of 573 K to the right side of the block (face 3).

model.FaceBC(1) = faceBC(Temperature=373);
model.FaceBC(3) = faceBC(Temperature=573);

Apply a heat flux boundary condition to the bottom of the block.

model.FaceLoad(4) = faceLoad(Heat=-20);

Mesh the geometry and solve the problem.

model = generateMesh(model);
R = solve(model)

R = 
  SteadyStateThermalResults with properties:

    Temperature: [12822x1 double]
     XGradients: [12822x1 double]
     YGradients: [12822x1 double]
     ZGradients: [12822x1 double]
           Mesh: [1x1 FEMesh]

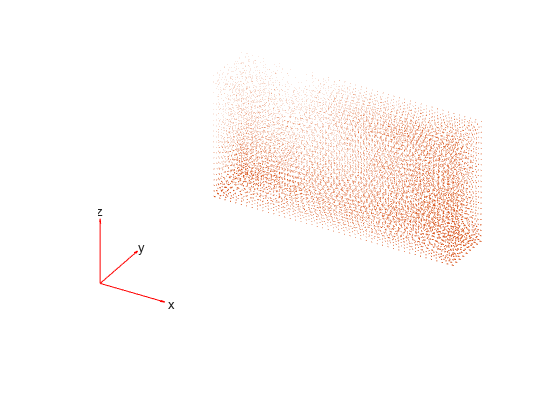
Evaluate heat flux at the nodal locations.

[qx,qy,qz] = evaluateHeatFlux(R);

figure
pdeplot3D(R.Mesh,FlowData=[qx qy qz])

Figure contains an axes object. The hidden axes object contains 5 objects of type quiver, text.

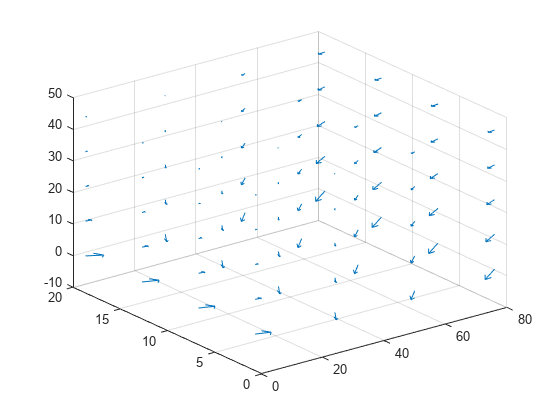
Create a grid specified by x, y, and z coordinates, and evaluate heat flux to the grid.

[X,Y,Z] = meshgrid(1:26:100,1:6:20,1:11:50);

[qx,qy,qz] = evaluateHeatFlux(R,X,Y,Z);

Reshape the qx, qy, and qz vectors, and plot the resulting heat flux.

qx = reshape(qx,size(X));
qy = reshape(qy,size(Y));
qz = reshape(qz,size(Z));
figure
quiver3(X,Y,Z,qx,qy,qz)

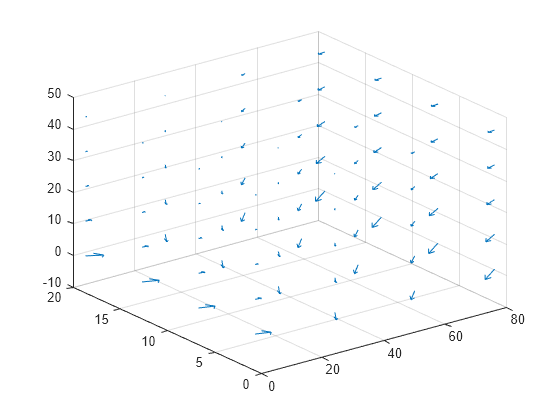
Figure contains an axes object. The axes object contains an object of type quiver.

Alternatively, you can specify the grid by using a matrix of query points.

querypoints = [X(:) Y(:) Z(:)]';
[qx,qy,qz] = evaluateHeatFlux(R,querypoints);

qx = reshape(qx,size(X));
qy = reshape(qy,size(Y));
qz = reshape(qz,size(Z));
figure
quiver3(X,Y,Z,qx,qy,qz)

Figure contains an axes object. The axes object contains an object of type quiver.

Solve 3-D Electrostatic Problem

Open Live Script

Solve an electromagnetic problem and find the electric potential and field distribution for a 3-D geometry representing a plate with a hole.

Create an femodel object for electrostatic analysis and include a geometry representing a plate with a hole.

model = femodel(AnalysisType="electrostatic", ...
                Geometry="PlateHoleSolid.stl");

Plot the geometry.

pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.3)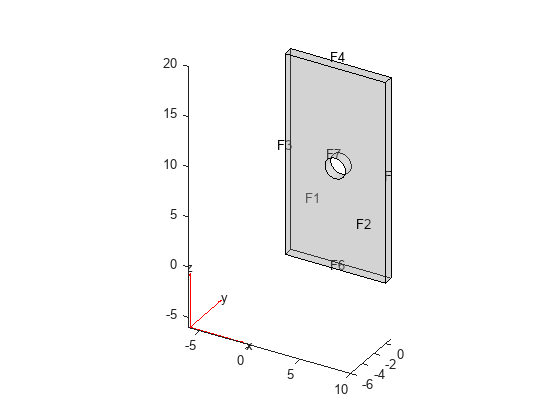

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Specify the vacuum permittivity in the SI system of units.

model.VacuumPermittivity = 8.8541878128E-12;

Specify the relative permittivity of the material.

model.MaterialProperties = ...
    materialProperties(RelativePermittivity=1);

Specify the charge density for the entire geometry.

model.CellLoad = cellLoad(ChargeDensity=5E-9);

Apply the voltage boundary conditions on the side faces and the face bordering the hole.

model.FaceBC(3:6) = faceBC(Voltage=0);
model.FaceBC(7) = faceBC(Voltage=1000);

Generate the mesh.

model = generateMesh(model);

Solve the model.

R = solve(model)

R = 
  ElectrostaticResults with properties:

      ElectricPotential: [4747x1 double]
          ElectricField: [1x1 FEStruct]
    ElectricFluxDensity: [1x1 FEStruct]
                   Mesh: [1x1 FEMesh]

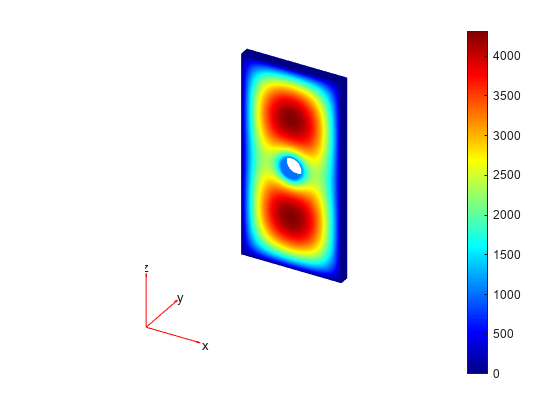
Plot the electric potential.

figure
pdeplot3D(R.Mesh,ColorMapData=R.ElectricPotential)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

Plot the electric field.

pdeplot3D(R.Mesh,FlowData=[R.ElectricField.Ex ...
                           R.ElectricField.Ey ...
                           R.ElectricField.Ez])

Figure contains an axes object. The hidden axes object contains 5 objects of type quiver, text.

Solution Plot on Surface

Open Live Script

Plot a PDE solution on the geometry surface. First, create a PDE model and import a 3-D geometry file. Specify boundary conditions and coefficients. Mesh the geometry and solve the problem.

model = createpde;
importGeometry(model,"Block.stl");
applyBoundaryCondition(model,"dirichlet",Face=1:4,u=0);
specifyCoefficients(model,m=0,d=0,c=1,a=0,f=2);
generateMesh(model);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [12822x1 double]
       XGradients: [12822x1 double]
       YGradients: [12822x1 double]
       ZGradients: [12822x1 double]
             Mesh: [1x1 FEMesh]

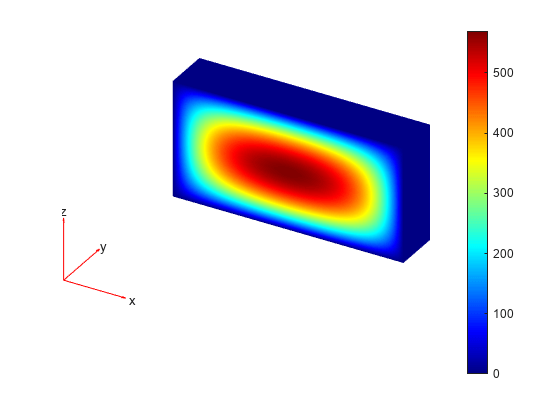
Plot the solution at the nodal locations on the geometry surface.

u = results.NodalSolution;
msh = results.Mesh;
pdeplot3D(msh,ColorMapData=u)

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

3-D Mesh Plot

Open Live Script

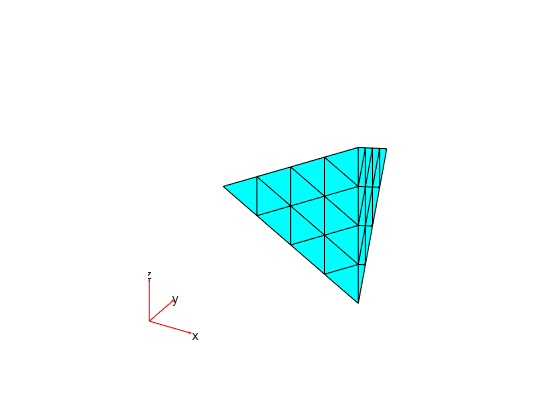
Import a geometry and generate a linear mesh.

gm = fegeometry("Tetrahedron.stl");
gm = generateMesh(gm,Hmax=20,GeometricOrder="linear");

Plot the mesh.

mesh = gm.Mesh;
pdeplot3D(mesh)

Figure contains an axes object. The hidden axes object contains 5 objects of type quiver, text, patch.

Alternatively, you can use the nodes and elements of the mesh as input arguments for pdeplot3D.

pdeplot3D(mesh.Nodes,mesh.Elements)

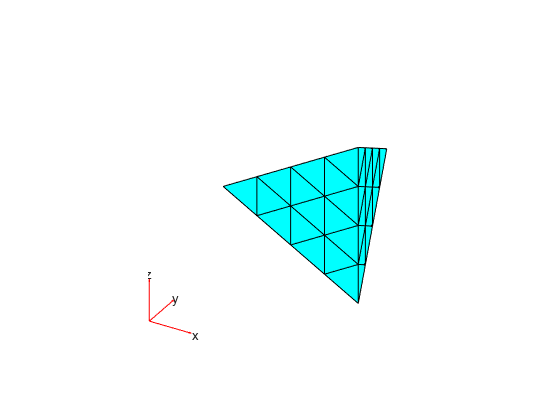
Figure contains an axes object. The hidden axes object contains 5 objects of type quiver, text, patch.

Display the node labels on the surface of a simple mesh.

pdeplot3D(mesh,NodeLabels="on")
view(101,12)

Figure contains an axes object. The hidden axes object contains 5 objects of type quiver, text, patch.

Display the element labels.

pdeplot3D(mesh,ElementLabels="on")
view(101,12)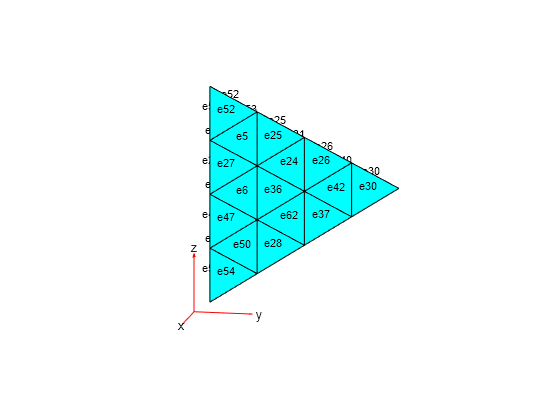

Figure contains an axes object. The hidden axes object contains 5 objects of type quiver, text, patch.

Input Arguments

collapse all

`model` — Model container
`PDEModel` object | `ThermalModel` object | `StructuralModel` object | `ElectromagneticModel` object

Model container, specified as a PDEModel object, ThermalModel object, StructuralModel object, or ElectromagneticModel object.

`mesh` — Mesh description
`FEMesh` object

Mesh description, specified as an FEMesh object.

`nodes` — Nodal coordinates
3-by-NumNodes matrix

Nodal coordinates, specified as a 3-by-NumNodes matrix. NumNodes is the number of nodes.

`elements` — Element connectivity matrix in terms of node IDs
4-by-NumElements matrix | 10-by-NumElements matrix

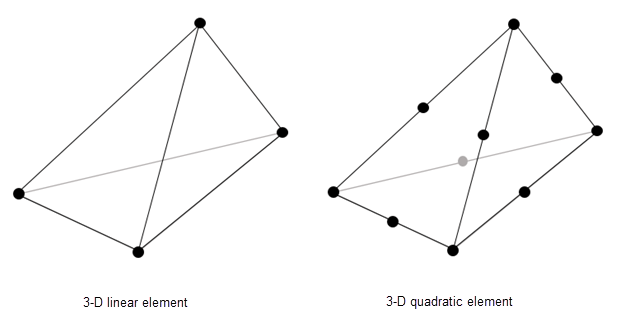
Element connectivity matrix in terms of the node IDs, specified as a 4-by-NumElements or 10-by-NumElements matrix. Linear meshes contain only corner nodes. For linear meshes, the connectivity matrix has four nodes per 3-D element. Quadratic meshes contain corner nodes and nodes in the middle of each edge of an element. For quadratic meshes, the connectivity matrix has 10 nodes per 3-D element.

A linear tetrahedral element with a node in each corner and a quadratic tetrahedral element with an additional node in the middle of each edge

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: pdeplot3D(model,NodeLabels="on")

`ColorMapData` — Data to plot as colored surface
column vector

Data to plot as a colored surface, specified as the comma-separated pair consisting of "ColorMapData" and a column vector with the number of elements that equals the number of points in the mesh. Typically, this data is the solution returned by solvepde for a scalar PDE problem and a component of the solution for a multicomponent PDE system.

Example: ColorMapData=results.NodalSolution

Example: ColorMapData=results.NodalSolution(:,1)

Data Types: double

`FlowData` — Data for quiver plot
matrix

Data for the quiver plot, specified as the comma-separated pair consisting of "FlowData" and an M-by-3 matrix, where M is the number of mesh nodes. FlowData contains the x, y, and z values of the field at the mesh points. Set FlowData as follows:

results = solvepde(model);
[cgradx,cgrady,cgradz] = evaluateCGradient(results);
pdeplot3D(results.Mesh,FlowData=[cgradx cgrady cgradz])

pdeplot3D plots the real part of complex data.

Example: FlowData=[cgradx cgrady cgradz]

Data Types: double

`Mesh` — Indicator to show mesh
`"off"` (default) | `"on"`

Indicator to show the mesh, specified as the comma-separated pair consisting of "Mesh" and "on" or "off". Specify "on" to show the mesh in the plot.

Example: Mesh="on"

Data Types: char | string

`NodeLabels` — Node labels
`"off"` (default) | `"on"`

Node labels, specified as the comma-separated pair consisting of "NodeLabels" and "off" or "on".

Example: NodeLabels="on"

Data Types: char | string

`ElementLabels` — Element labels
`"off"` (default) | `"on"`

Element labels, specified as the comma-separated pair consisting of "ElementLabels" and "off" or "on".

Example: ElementLabels="on"

Data Types: char | string

`FaceAlpha` — Surface transparency for 3-D geometry
`1` (default) | real number from `0` through `1`

Surface transparency for 3-D geometry, specified as a real number from 0 through 1. The default value 1 indicates no transparency. The value 0 indicates complete transparency.

Example: FaceAlpha=0.5

Data Types: double

`Deformation` — Deformed shape for structural analysis models
`FEStruct` object representing displacement values at nodes

Deformed shape for structural analysis models, specified as the comma-separated pair consisting of Deformation and the FEStruct object representing displacement values at nodes. The displacement FEStruct object is a property of StaticStructuralResults, TransientStructuralResults, and FrequencyStructuralResults.

In an undeformed shape, center nodes in quadratic meshes are always added at half-distance between corners. When you plot a deformed shape, the center nodes might move away from the edge centers.

Example: Deformation=results.Displacement

`DeformationScaleFactor` — Scaling factor for plotting deformed shape
positive number

Scaling factor for plotting the deformed shape, specified as the comma-separated pair consisting of DeformationScaleFactor and a positive number. Use this argument together with the Deformation name-value pair argument. The pdeplot3D function chooses the default value based on the geometry itself and on the magnitude of deformation.

Example: DeformationScaleFactor=1000

Data Types: double

Output Arguments

collapse all

`h` — Handles to graphics objects
vector

Handles to graphics objects, returned as a vector.

Version History

Introduced in R2015a

expand all

R2023a: Finite element model

pdeplot3d accepts the femodel object that defines structural mechanics, thermal, and electromagnetic problems.

R2021b: Electromagnetic Analysis

You can now plot electromagnetic results, such as electric and magnetic potentials, fields, and fluxes.

R2020a: Improved performance for plots with many text labels

pdeplot3d shows faster rendering and better responsiveness for plots that display many text labels. Code containing findobj(fig,'Type','Text') no longer returns labels on figures produced by pdeplot3d.

R2018a: Highlighting particular nodes and elements on mesh plots

pdeplot3d accepts node and element IDs as input arguments, letting you highlight particular nodes and elements on mesh plots.

R2017b: Structural Analysis

You can now plot structural results, such as displacements, stresses, and strains.

R2017a: Thermal Analysis

You can now plot thermal results, such as temperatures and temperature gradients.

R2016b: Transparency, node and element labels

You can now set plot transparency by using FaceAlpha, and display node and element labels by using NodeLabels and ElementLabels, respectively.

pdeplot3D

Syntax

Description

Examples

Deformed Shape for Cantilever Beam Problem

von Mises Stress for 3-D Structural Dynamic Problem

Solve Steady-State Thermal Problem

Heat Flux for 3-D Steady-State Thermal Problem

Solve 3-D Electrostatic Problem

Solution Plot on Surface

3-D Mesh Plot

Input Arguments

`model` — Model container
`PDEModel` object | `ThermalModel` object | `StructuralModel` object | `ElectromagneticModel` object

`mesh` — Mesh description
`FEMesh` object

`nodes` — Nodal coordinates
3-by-NumNodes matrix

`elements` — Element connectivity matrix in terms of node IDs
4-by-NumElements matrix | 10-by-NumElements matrix

Name-Value Arguments

`ColorMapData` — Data to plot as colored surface
column vector

`FlowData` — Data for quiver plot
matrix

`Mesh` — Indicator to show mesh
`"off"` (default) | `"on"`

`NodeLabels` — Node labels
`"off"` (default) | `"on"`

`ElementLabels` — Element labels
`"off"` (default) | `"on"`

`FaceAlpha` — Surface transparency for 3-D geometry
`1` (default) | real number from `0` through `1`

`Deformation` — Deformed shape for structural analysis models
`FEStruct` object representing displacement values at nodes

`DeformationScaleFactor` — Scaling factor for plotting deformed shape
positive number

Output Arguments

`h` — Handles to graphics objects
vector

Version History

R2023a: Finite element model

R2021b: Electromagnetic Analysis

R2020a: Improved performance for plots with many text labels

R2018a: Highlighting particular nodes and elements on mesh plots

R2017b: Structural Analysis

R2017a: Thermal Analysis

R2016b: Transparency, node and element labels

See Also

Topics

pdeplot3D

Syntax

Description

Examples

Deformed Shape for Cantilever Beam Problem

von Mises Stress for 3-D Structural Dynamic Problem

Solve Steady-State Thermal Problem

Heat Flux for 3-D Steady-State Thermal Problem

Solve 3-D Electrostatic Problem

Solution Plot on Surface

3-D Mesh Plot

Input Arguments

model — Model container PDEModel object | ThermalModel object | StructuralModel object | ElectromagneticModel object

mesh — Mesh description FEMesh object

nodes — Nodal coordinates 3-by-NumNodes matrix

elements — Element connectivity matrix in terms of node IDs 4-by-NumElements matrix | 10-by-NumElements matrix

Name-Value Arguments

ColorMapData — Data to plot as colored surface column vector

FlowData — Data for quiver plot matrix

Mesh — Indicator to show mesh "off" (default) | "on"

NodeLabels — Node labels "off" (default) | "on"

ElementLabels — Element labels "off" (default) | "on"

FaceAlpha — Surface transparency for 3-D geometry 1 (default) | real number from 0 through 1

Deformation — Deformed shape for structural analysis models FEStruct object representing displacement values at nodes

DeformationScaleFactor — Scaling factor for plotting deformed shape positive number

Output Arguments

h — Handles to graphics objects vector

Version History

R2023a: Finite element model

R2021b: Electromagnetic Analysis

R2020a: Improved performance for plots with many text labels

R2018a: Highlighting particular nodes and elements on mesh plots

R2017b: Structural Analysis

R2017a: Thermal Analysis

R2016b: Transparency, node and element labels

See Also

Topics

`model` — Model container
`PDEModel` object | `ThermalModel` object | `StructuralModel` object | `ElectromagneticModel` object

`mesh` — Mesh description
`FEMesh` object

`nodes` — Nodal coordinates
3-by-NumNodes matrix

`elements` — Element connectivity matrix in terms of node IDs
4-by-NumElements matrix | 10-by-NumElements matrix

`ColorMapData` — Data to plot as colored surface
column vector

`FlowData` — Data for quiver plot
matrix

`Mesh` — Indicator to show mesh
`"off"` (default) | `"on"`

`NodeLabels` — Node labels
`"off"` (default) | `"on"`

`ElementLabels` — Element labels
`"off"` (default) | `"on"`

`FaceAlpha` — Surface transparency for 3-D geometry
`1` (default) | real number from `0` through `1`

`Deformation` — Deformed shape for structural analysis models
`FEStruct` object representing displacement values at nodes

`DeformationScaleFactor` — Scaling factor for plotting deformed shape
positive number

`h` — Handles to graphics objects
vector