pdeplot

Plot solution or mesh for 2-D problem

collapse all in page

Syntax

pdeplot(results.Mesh,XYData=results.Temperature,ColorMap="hot")

pdeplot(results.Mesh,XYData=results.VonMisesStress,Deformation=results.Displacement)

pdeplot(results.Mesh,XYData=results.ModeShapes.ux)

pdeplot(results.Mesh,XYData=results.ElectricPotential)

pdeplot(results.Mesh,XYData=results.NodalSolution)

pdeplot(mesh)

pdeplot(nodes,elements)

pdeplot(model)

pdeplot(p,e,t)

pdeplot(___,Name,Value)

h = pdeplot(___)

Description

pdeplot(results.Mesh,XYData=results.Temperature,ColorMap="hot") plots the temperature at nodal locations for a 2-D thermal analysis problem. This syntax creates a colored surface plot using the "hot" colormap.

example

pdeplot(results.Mesh,XYData=results.VonMisesStress,Deformation=results.Displacement) plots the von Mises stress and shows the deformed shape for a 2-D structural analysis problem.

example

pdeplot(results.Mesh,XYData=results.ModeShapes.ux) plots the x-component of the modal displacement for a 2-D structural modal analysis problem.

example

pdeplot(results.Mesh,XYData=results.ElectricPotential) plots the electric potential at nodal locations for a 2-D electrostatic analysis problem.

example

pdeplot(results.Mesh,XYData=results.NodalSolution) plots the solution at nodal locations as a colored surface plot using the default colormap.

example

pdeplot(mesh) plots the mesh.

example

pdeplot(nodes,elements) plots the mesh defined by its nodes and elements.

example

pdeplot(model) plots the mesh specified in model. This syntax does not work with an femodel object.

pdeplot(p,e,t) plots the mesh described by p,e, and t.

pdeplot(___,Name,Value) plots the mesh, the data at the nodal locations, or both the mesh and the data, using the Name,Value pair arguments. Use any arguments from the previous syntaxes.

Specify at least one of the FlowData (vector field plot), XYData (colored surface plot), or ZData (3-D height plot) name-value pairs. You can combine any number of plot types.

For a thermal analysis, you can plot temperature or gradient of temperature.
For a structural analysis, you can plot displacement, stress, strain, and von Mises stress. In addition, you can show the deformed shape and specify the scaling factor for the deformation plot.
For an electromagnetic analysis, you can plot electric or magnetic potentials, fields, and flux densities.

example

h = pdeplot(___) returns a handle to a plot, using any of the previous syntaxes.

example

Examples

collapse all

Solve Transient Thermal Problem

Open Live Script

Solve a 2-D transient thermal problem.

Create a geometry representing a square plate with a diamond-shaped region in its center.

SQ1 = [3; 4; 0; 3; 3; 0; 0; 0; 3; 3];
D1 = [2; 4; 0.5; 1.5; 2.5; 1.5; 1.5; 0.5; 1.5; 2.5];
gd = [SQ1 D1];
sf = 'SQ1+D1';
ns = char('SQ1','D1');
ns = ns';
g = decsg(gd,sf,ns);
pdegplot(g,EdgeLabels="on",FaceLabels="on")
xlim([-1.5 4.5])
ylim([-0.5 3.5])
axis equal

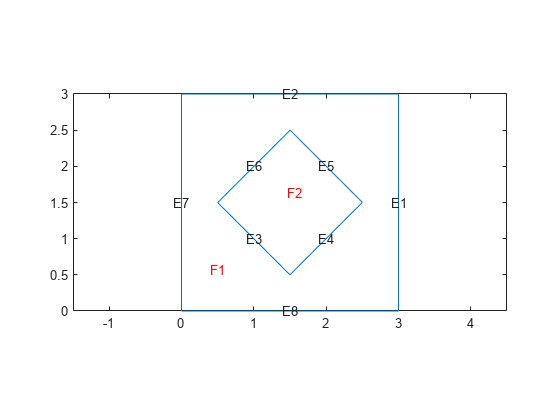
Figure contains an axes object. The axes object contains 11 objects of type line, text.

Create an femodel object for transient thermal analysis and include the geometry.

model = femodel(AnalysisType="thermalTransient", ...
                Geometry=g);

For the square region, assign these thermal properties:

Thermal conductivity is $10 W / (m \cdot^{\circ} C)$
Mass density is $2 kg / m^{3}$
Specific heat is $0.1 J / ({kg \cdot}^{\circ} C)$

model.MaterialProperties(1) = ...
    materialProperties(ThermalConductivity=10, ...
                       MassDensity=2, ...
                       SpecificHeat=0.1);

For the diamond region, assign these thermal properties:

Thermal conductivity is $2 W / (m \cdot^{\circ} C)$
Mass density is $1 kg / m^{3}$
Specific heat is $0.1 J / ({kg \cdot}^{\circ} C)$

model.MaterialProperties(2) = ...
    materialProperties(ThermalConductivity=2, ...
                       MassDensity=1, ...
                       SpecificHeat=0.1);

Assume that the diamond-shaped region is a heat source with a density of $4 W / m^{2}$ .

model.FaceLoad(2) = faceLoad(Heat=4);

Apply a constant temperature of 0 °C to the sides of the square plate.

model.EdgeBC([1 2 7 8]) = edgeBC(Temperature=0);

Set the initial temperature to 0 °C.

model.FaceIC = faceIC(Temperature=0);

Generate the mesh.

model = generateMesh(model);

The dynamics for this problem are very fast. The temperature reaches a steady state in about 0.1 second. To capture the most active part of the dynamics, set the solution time to logspace(-2,-1,10). This command returns 10 logarithmically spaced solution times between 0.01 and 0.1.

tlist = logspace(-2,-1,10);

Solve the equation.

thermalresults = solve(model,tlist);

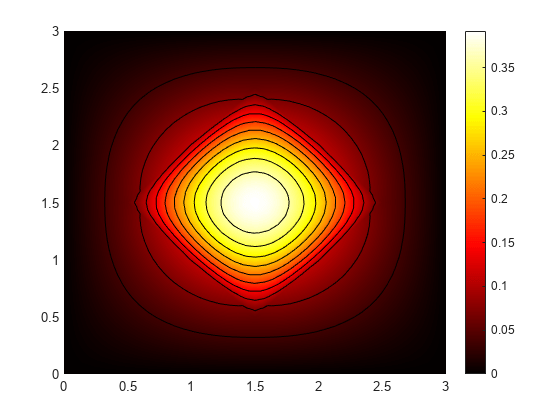
Plot the solution with isothermal lines by using a contour plot.

T = thermalresults.Temperature;
msh = thermalresults.Mesh;
pdeplot(msh,XYData=T(:,10),Contour="on",ColorMap="hot")

Figure contains an axes object. The axes object contains 12 objects of type patch, line.

Plot Deformed Shape for Static Plane-Strain Problem

Open Live Script

Create an femodel object for structural analysis and include the unit square geometry in the model.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry=@squareg);

Plot the geometry.

pdegplot(model.Geometry,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Specify Young's modulus and Poisson's ratio.

model.MaterialProperties = ...
    materialProperties(PoissonsRatio=0.3, ...
                       YoungsModulus=210E3);

Specify the x-component of the enforced displacement for edge 1.

model.EdgeBC(1) = edgeBC(XDisplacement=0.001);

Specify that edge 3 is a fixed boundary.

model.EdgeBC(3) = edgeBC(Constraint="fixed");

Generate a mesh and solve the problem.

model = generateMesh(model);
R = solve(model);

Plot the deformed shape using the default scale factor. By default, pdeplot internally determines the scale factor based on the dimensions of the geometry and the magnitude of deformation.

pdeplot(R.Mesh, ...
        XYData=R.VonMisesStress, ...
        Deformation=R.Displacement, ...
        ColorMap="jet")

Figure contains an axes object. The axes object contains an object of type patch.

Plot the deformed shape with the scale factor 500.

pdeplot(R.Mesh, ...
        XYData=R.VonMisesStress, ...
        Deformation=R.Displacement, ...
        DeformationScaleFactor=500,...
        ColorMap="jet")

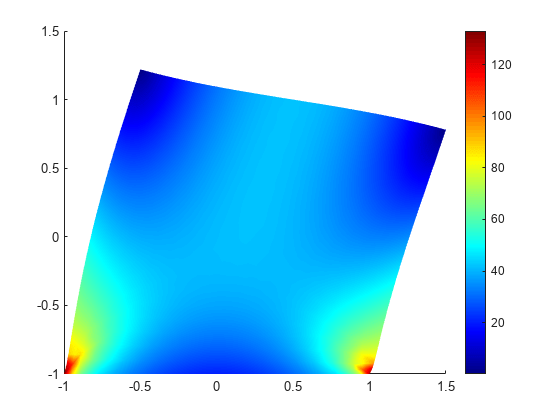
Figure contains an axes object. The axes object contains an object of type patch.

Plot the deformed shape without scaling.

pdeplot(R.Mesh, ...
        XYData=R.VonMisesStress, ...
        ColorMap="jet")

Figure contains an axes object. The axes object contains an object of type patch.

Solve Modal Structural Analysis Problem

Open Live Script

Find the fundamental (lowest) mode of a 2-D cantilevered beam, assuming prevalence of the plane-stress condition.

Specify geometric and structural properties of the beam, along with a unit plane-stress thickness.

length = 5;
height = 0.1;
E = 3E7;
nu = 0.3;
rho = 0.3/386;

Create a geometry.

gdm = [3;4;0;length;length;0;0;0;height;height];
g = decsg(gdm,'S1',('S1')');

Create an femodel object for modal structural analysis and include the geometry.

model = femodel(Analysistype="structuralModal", ...
                Geometry=g);

Define a maximum element size (five elements through the beam thickness).

hmax = height/5;

Generate a mesh.

model=generateMesh(model,Hmax=hmax);

Specify the structural properties and boundary constraints.

model.MaterialProperties = ...
    materialProperties(YoungsModulus=E, ...
                       MassDensity=rho, ... 
                       PoissonsRatio=nu);
model.EdgeBC(4) = edgeBC(Constraint="fixed");

Compute the analytical fundamental frequency (Hz) using the beam theory.

I = height^3/12;
analyticalOmega1 = 3.516*sqrt(E*I/(length^4*(rho*height)))/(2*pi)

analyticalOmega1 = 
126.9498

Specify a frequency range that includes an analytically computed frequency and solve the model.

R = solve(model,FrequencyRange=[0,1e6])

R = 
  ModalStructuralResults with properties:

    NaturalFrequencies: [32x1 double]
            ModeShapes: [1x1 FEStruct]
                  Mesh: [1x1 FEMesh]

The solver finds natural frequencies and modal displacement values at nodal locations. To access these values, use R.NaturalFrequencies and R.ModeShapes.

R.NaturalFrequencies/(2*pi)

R.ModeShapes

ans = 
  FEStruct with properties:

           ux: [6511x32 double]
           uy: [6511x32 double]
    Magnitude: [6511x32 double]

Plot the y-component of the solution for the fundamental frequency.

pdeplot(R.Mesh,XYData=R.ModeShapes.uy(:,1))
title(['First Mode with Frequency ', ...
        num2str(R.NaturalFrequencies(1)/(2*pi)),' Hz'])
axis equal

Figure contains an axes object. The axes object with title First Mode with Frequency 126.9416 Hz contains an object of type patch.

Solve 2-D Electrostatic Problem

Open Live Script

Solve an electromagnetic problem and find the electric potential and field distribution for a 2-D geometry representing a plate with a hole.

Create an femodel object for electrostatic analysis and include a geometry representing a plate with a hole.

model = femodel(AnalysisType="electrostatic",...
                Geometry="PlateHolePlanar.stl");

Plot the geometry with edge labels.

pdegplot(model.Geometry,EdgeLabels="on")

Figure contains an axes object. The axes object contains an object of type line.

Specify the vacuum permittivity value in the SI system of units.

model.VacuumPermittivity = 8.8541878128E-12;

Specify the relative permittivity of the material.

model.MaterialProperties = ...
    materialProperties(RelativePermittivity=1);

Apply the voltage boundary conditions on the edges framing the rectangle and the circle.

model.EdgeBC(1:4) = edgeBC(Voltage=0);
model.EdgeBC(5) = edgeBC(Voltage=1000);

Specify the charge density for the entire geometry.

model.FaceLoad = faceLoad(ChargeDensity=5E-9);

Generate the mesh.

model = generateMesh(model);

Solve the model.

R = solve(model)

R = 
  ElectrostaticResults with properties:

      ElectricPotential: [1231x1 double]
          ElectricField: [1x1 FEStruct]
    ElectricFluxDensity: [1x1 FEStruct]
                   Mesh: [1x1 FEMesh]

Plot the electric potential and field.

pdeplot(R.Mesh,XYData=R.ElectricPotential, ...
               FlowData=[R.ElectricField.Ex ...
                         R.ElectricField.Ey])
axis equal

Figure contains an axes object. The axes object contains 2 objects of type patch, quiver.

Plot General PDE Solution

Open Live Script

Create colored 2-D and 3-D plots of a solution to a PDE model.

Create a PDE model. Include the geometry of the built-in function lshapeg. Mesh the geometry.

model = createpde;
geometryFromEdges(model,@lshapeg);
generateMesh(model);

Set the zero Dirichlet boundary conditions on all edges.

applyBoundaryCondition(model,"dirichlet", ...
                             Edge=1:model.Geometry.NumEdges, ...
                             u=0);

Specify the coefficients and solve the PDE.

specifyCoefficients(model,m=0, ...
                          d=0, ...
                          c=1, ...
                          a=0, ...
                          f=1);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [1141x1 double]
       XGradients: [1141x1 double]
       YGradients: [1141x1 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Plot the 2-D solution at the nodal locations.

u = results.NodalSolution;
msh = results.Mesh;
pdeplot(msh,XYData=u)

Figure contains an axes object. The axes object contains an object of type patch.

Plot the 3-D solution.

pdeplot(msh,XYData=u,ZData=u)

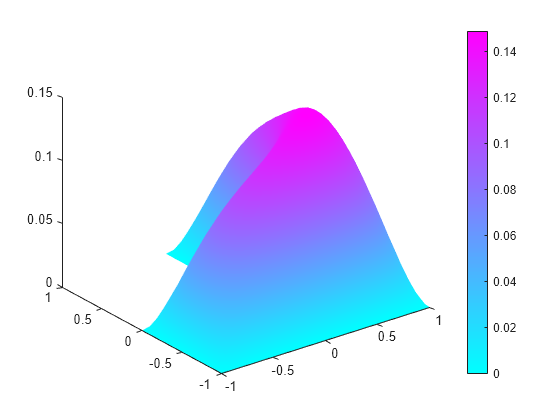
Figure contains an axes object. The axes object contains an object of type patch.

Plot Gradient of General PDE Solution

Open Live Script

Plot the gradient of a PDE solution as a quiver plot.

Create a PDE model. Include the geometry of the built-in function lshapeg. Mesh the geometry.

model = createpde;
geometryFromEdges(model,@lshapeg);
generateMesh(model);

Set the zero Dirichlet boundary conditions on all edges.

applyBoundaryCondition(model,"dirichlet", ...
                             Edge=1:model.Geometry.NumEdges, ...
                             u=0);

Specify coefficients and solve the PDE.

specifyCoefficients(model,m=0, ...
                          d=0, ...
                          c=1, ...
                          a=0, ...
                          f=1);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [1141x1 double]
       XGradients: [1141x1 double]
       YGradients: [1141x1 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Plot the gradient of the solution at the nodal locations as a quiver plot.

ux = results.XGradients;
uy = results.YGradients;
msh = results.Mesh;
pdeplot(msh,FlowData=[ux,uy])

Figure contains an axes object. The axes object contains an object of type quiver.

Plot General PDE Solution and Its Gradient

Open Live Script

Plot the solution of a 2-D PDE in 3-D with the "jet" coloring and a mesh, and include a quiver plot. Get handles to the axes objects.

Create a PDE model. Include the geometry of the built-in function lshapeg. Mesh the geometry.

model = createpde;
geometryFromEdges(model,@lshapeg);
generateMesh(model);

Set zero Dirichlet boundary conditions on all edges.

applyBoundaryCondition(model,"dirichlet", ...
                             Edge=1:model.Geometry.NumEdges, ...
                             u=0);

Specify coefficients and solve the PDE.

specifyCoefficients(model,m=0, ...
                          d=0, ...
                          c=1, ...
                          a=0, ...
                          f=1);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [1141x1 double]
       XGradients: [1141x1 double]
       YGradients: [1141x1 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Plot the solution in 3-D with the "jet" coloring and a mesh, and include the gradient as a quiver plot.

u = results.NodalSolution;
ux = results.XGradients;
uy = results.YGradients;
msh = results.Mesh;
h = pdeplot(msh,XYData=u,ZData=u, ...
                FaceAlpha=0.5, ...
                FlowData=[ux,uy], ...
                ColorMap="jet", ...
                Mesh="on");

Figure contains an axes object. The axes object contains 2 objects of type patch, quiver.

Plot 2-D Mesh

Open Live Script

Create an femodel object and include the geometry of the built-in function lshapeg.

model = femodel(Geometry=@lshapeg);

Generate and plot the mesh.

model = generateMesh(model);
msh = model.Geometry.Mesh;
pdeplot(msh)

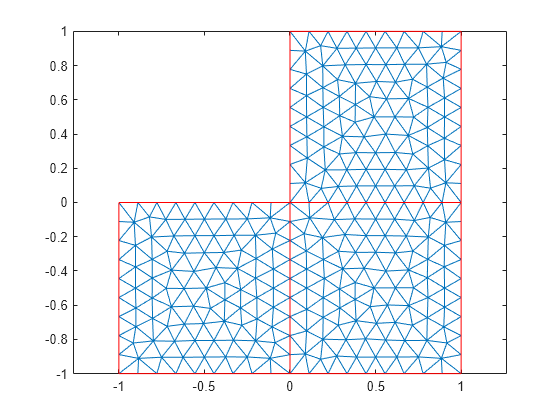
Figure contains an axes object. The axes object contains 2 objects of type line.

Alternatively, you can use the nodes and elements of the mesh as input arguments for pdeplot.

pdeplot(msh.Nodes,msh.Elements)

Figure contains an axes object. The axes object contains an object of type line.

Display the node labels. Use xlim and ylim to zoom in on particular nodes.

pdeplot(msh,NodeLabels="on")
xlim([-0.2,0.2])
ylim([-0.2,0.2])

Figure contains an axes object. The axes object contains 2 objects of type line.

Display the element labels.

pdeplot(msh,ElementLabels="on")
xlim([-0.2,0.2])
ylim([-0.2,0.2])

Figure contains an axes object. The axes object contains 2 objects of type line.

Input Arguments

collapse all

`mesh` — Mesh description
`FEMesh` object

Mesh description, specified as an FEMesh object.

`nodes` — Nodal coordinates
2-by-NumNodes matrix

Nodal coordinates, specified as a 2-by-NumNodes matrix. NumNodes is the number of nodes.

`elements` — Element connectivity matrix in terms of node IDs
3-by-NumElements matrix | 6-by-NumElements matrix

Element connectivity matrix in terms of the node IDs, specified as a 3-by-NumElements or 6-by-NumElements matrix. Linear meshes contain only corner nodes. For linear meshes, the connectivity matrix has three nodes per 2-D element. Quadratic meshes contain corner nodes and nodes in the middle of each edge of an element. For quadratic meshes, the connectivity matrix has six nodes per 2-D element.

A linear triangular element with a node in each corner and a quadratic triangular element with an additional node in the middle of each edge

`model` — Model object
`PDEModel` object | `ThermalModel` object | `StructuralModel` object | `ElectromagneticModel` object

Model object, specified as a PDEModel object, ThermalModel object, StructuralModel object, or ElectromagneticModel object.

`p` — Mesh points
matrix

Mesh points, specified as a 2-by-Np matrix of points, where Np is the number of points in the mesh. For a description of the (p,e,t) matrices, see Mesh Data as [p,e,t] Triples.

Typically, you use the p, e, and t data exported from the PDE Modeler app, or generated by initmesh or refinemesh.

Example: [p,e,t] = initmesh(gd)

Data Types: double

`e` — Mesh edges
matrix

Mesh edges, specified as a 7-by-Ne matrix of edges, where Ne is the number of edges in the mesh. For a description of the (p,e,t) matrices, see Mesh Data as [p,e,t] Triples.

Typically, you use the p, e, and t data exported from the PDE Modeler app, or generated by initmesh or refinemesh.

Example: [p,e,t] = initmesh(gd)

Data Types: double

`t` — Mesh triangles
matrix

Mesh triangles, specified as a 4-by-Nt matrix of triangles, where Nt is the number of triangles in the mesh. For a description of the (p,e,t) matrices, see Mesh Data as [p,e,t] Triples.

Typically, you use the p, e, and t data exported from the PDE Modeler app, or generated by initmesh or refinemesh.

Example: [p,e,t] = initmesh(gd)

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: pdeplot(results.Mesh,XYData=u,ZData=u)

Tip

Specify at least one of the FlowData (vector field plot), XYData (colored surface plot), or ZData (3-D height plot) name-value pairs. Otherwise, pdeplot plots the mesh with no data.

Data Plots

collapse all

`XYData` — Colored surface plot data
vector

Colored surface plot data, specified as a vector. If you use a [p,e,t] representation, specify data for points in a vector of length size(p,2), or specify data for triangles in a vector of length size(t,2).

Typically, you set XYData to the solution u. The pdeplot function uses XYData for coloring both 2-D and 3-D plots.
pdeplot uses the colormap specified in the ColorMap name-value pair, using the style specified in the XYStyle name-value pair.
When the Contour name-value pair is "on", pdeplot also plots level curves of XYData.
pdeplot plots the real part of complex data.

To plot the kth component of a solution to a PDE system, extract the relevant part of the solution, for example:

results = solvepde(model);
u = results.NodalSolution; % each column of u has one component of u
pdeplot(results.Mesh,XYData=u(:,k)) % data for column k

Example: XYData=u

Data Types: double

`XYStyle` — Coloring choice
`"interp"` (default) | `"off"` | `"flat"`

Coloring choice, specified as one of the following values:

"off" — No shading, only mesh is displayed.
"flat" — Each triangle in the mesh has a uniform color.
"interp" — Plot coloring is smoothly interpolated.

The coloring choice relates to the XYData name-value pair.

Example: XYStyle="flat"

Data Types: char | string

`ZData` — Data for 3-D plot heights
matrix

Data for the 3-D plot heights, specified as a matrix. If you use a [p,e,t] representation, provide data for points in a vector of length size(p,2) or data for triangles in a vector of length size(t,2).

Typically, you set ZData to u, the solution. The XYData name-value pair sets the coloring of the 3-D plot.
The ZStyle name-value pair specifies whether the plot is continuous or discontinuous.
pdeplot plots the real part of complex data.

To plot the kth component of a solution to a PDE system, extract the relevant part of the solution, for example:

results = solvepde(model);
u = results.NodalSolution; % each column of u has one component of u
pdeplot(results.Mesh,XYData=u(:,k),ZData=u(:,k)) % data for column k

Example: ZData=u

Data Types: double

`ZStyle` — 3-D plot style
`"continuous"` (default) | `"off"` | `"discontinuous"`

3-D plot style, specified as one of these values:

"off" — No 3-D plot.
"discontinuous" — Each triangle in the mesh has a uniform height in a 3-D plot.
"continuous" — 3-D surface plot is continuous.

If you use ZStyle without specifying the ZData name-value pair, then pdeplot ignores ZStyle.

Example: ZStyle="discontinuous"

Data Types: char | string

`FlowData` — Data for quiver plot
matrix

Data for the quiver plot, specified as an M-by-2 matrix, where M is the number of mesh nodes. FlowData contains the x and y values of the field at the mesh points.

When you use ZData to represent a 2-D PDE solution as a 3-D plot and you also include a quiver plot, the quiver plot appears in the z = 0 plane.

pdeplot plots the real part of complex data.

Example: FlowData=[ux uy]

Data Types: double

`FlowStyle` — Indicator to show quiver plot
`"arrow"` (default) | `"off"`

Indicator to show the quiver plot, specified as "arrow" or "off". Here, "arrow" displays the quiver plot specified by the FlowData name-value pair.

Example: FlowStyle="off"

Data Types: char | string

`XYGrid` — Indicator to convert mesh data to x-y grid
`"off"` (default) | `"on"`

Indicator to convert the mesh data to x-y grid before plotting, specified as "off" or "on".

Note

This conversion can change the geometry and lessen the quality of the plot.

By default, the grid has about sqrt(size(t,2)) elements in each direction.

Example: XYGrid="on"

Data Types: char | string

`GridParam` — Customized x-y grid
`[tn;a2;a3]` from an earlier call to `tri2grid`

Customized x-y grid, specified as a matrix [tn;a2;a3]. For example:

[~,tn,a2,a3] = tri2grid(p,t,u,x,y);
pdeplot(p,e,t,XYGrid="on",GridParam=[tn;a2;a3],XYData=u)

For details on the grid data and its x and y arguments, see tri2grid. The tri2grid function does not work with PDEModel objects.

Example: GridParam=[tn;a2;a3]

Data Types: double

Mesh Plots

collapse all

`NodeLabels` — Node labels
`"off"` (default) | `"on"`

Node labels, specified as "off" or "on".

pdeplot ignores NodeLabels when you use it with ZData.

Example: NodeLabels="on"

Data Types: char | string

`ElementLabels` — Element labels
`"off"` (default) | `"on"`

Element labels, specified as "off" or "on".

pdeplot ignores ElementLabels when you use it with ZData.

Example: ElementLabels="on"

Data Types: char | string

Structural Analysis Plots

collapse all

`Deformation` — Data for plotting deformed shape
`Displacement` property of `StaticStructuralResults` object

Data for plotting the deformed shape for a structural analysis model, specified as the Displacement property of the StaticStructuralResults object.

In an undeformed shape, center nodes in quadratic meshes are always added at half-distance between corners. When you plot a deformed shape, the center nodes might move away from the edge centers.

Example: Deformation = structuralresults.Displacement

`DeformationScaleFactor` — Scaling factor for plotting deformed shape
real number

Scaling factor for plotting the deformed shape, specified as a real number. Use this argument with the Deformation name-value pair. The default value is defined internally, based on the dimensions of the geometry and the magnitude of the deformation.

Example: DeformationScaleFactor=100

Data Types: double

Annotations and Appearance

collapse all

`ColorBar` — Indicator to include color bar
`"on"` (default) | `"off"`

Indicator to include a color bar, specified as "on" or "off". Specify "on" to display a bar giving the numeric values of colors in the plot. For details, see colorbar. The pdeplot function uses the colormap specified in the ColorMap name-value pair.

Example: ColorBar="off"

Data Types: char | string

`ColorMap` — Colormap
`"cool"` (default) | `ColorMap` value or matrix of such values

Colormap, specified as a value representing a built-in colormap, or a colormap matrix. For details, see colormap.

ColorMap must be used with the XYData name-value pair.

Example: ColorMap="jet"

Data Types: double | char | string

`Mesh` — Indicator to show mesh
`"off"` (default) | `"on"`

Indicator to show the mesh, specified as "on" or "off". Specify "on" to show the mesh in the plot.

Example: Mesh="on"

Data Types: char | string

`Title` — Title of plot
string scalar | character vector

Title of plot, specified as a string scalar or character vector.

Example: Title="Solution Plot"

Data Types: char | string

`FaceAlpha` — Surface transparency for 3-D geometry
`1` (default) | real number from `0` through `1`

Surface transparency for 3-D geometry, specified as a real number from 0 through 1. The default value 1 indicates no transparency. The value 0 indicates complete transparency.

Example: FaceAlpha=0.5

Data Types: double

`Contour` — Indicator to plot level curves
`"off"` (default) | `"on"`

Indicator to plot level curves, specified as "off" or "on". Specify "on" to plot level curves for the XYData data. Specify the levels with the Levels name-value pair.

Example: Contour="on"

Data Types: char | string

`Levels` — Levels for contour plot
`10` (default) | positive integer | vector of level values

Levels for contour plot, specified as a positive integer or a vector of level values.

Positive integer — Plot Levels as equally spaced contours.
Vector — Plot contours at the values in Levels.

To obtain a contour plot, set the Contour name-value pair to "on".

Example: Levels=16

Data Types: double

Output Arguments

collapse all

`h` — Handles to graphics objects
vector

Handles to graphics objects, returned as a vector.

More About

collapse all

Quiver Plot

A quiver plot is a plot of a vector field. It is also called a flow plot.

Arrows show the direction of the field, with the lengths of the arrows showing the relative sizes of the field strength. For details on quiver plots, see quiver.

Version History

Introduced before R2006a

expand all

R2021a: Electromagnetic Analysis

You can now plot electromagnetic results, such as electric and magnetic potentials, fields, and fluxes.

R2020a: Improved performance for plots with many text labels

pdeplot shows faster rendering and better responsiveness for plots that display many text labels. Code containing findobj(fig,'Type','Text') no longer returns labels on figures produced by pdeplot.

R2018a: Highlighting particular nodes and elements on mesh plots

pdeplot accepts node and element IDs as input arguments, letting you highlight particular nodes and elements on mesh plots.

R2017b: Structural Analysis

You can now plot structural results, such as displacements, stresses, and strains.

R2017a: Thermal Analysis

You can now plot thermal results, such as temperatures and temperature gradients.

R2016b: Transparency, node and element labels

You can now set plot transparency by using FaceAlpha, and display node and element labels by using NodeLabels and ElementLabels, respectively.

pdeplot

Syntax

Description

Examples

Solve Transient Thermal Problem

Plot Deformed Shape for Static Plane-Strain Problem

Solve Modal Structural Analysis Problem

Solve 2-D Electrostatic Problem

Plot General PDE Solution

Plot Gradient of General PDE Solution

Plot General PDE Solution and Its Gradient

Plot 2-D Mesh

Input Arguments

mesh — Mesh description FEMesh object

nodes — Nodal coordinates 2-by-NumNodes matrix

elements — Element connectivity matrix in terms of node IDs 3-by-NumElements matrix | 6-by-NumElements matrix

model — Model object PDEModel object | ThermalModel object | StructuralModel object | ElectromagneticModel object

p — Mesh points matrix

e — Mesh edges matrix

t — Mesh triangles matrix

Name-Value Arguments

XYData — Colored surface plot data vector

XYStyle — Coloring choice "interp" (default) | "off" | "flat"

ZData — Data for 3-D plot heights matrix

ZStyle — 3-D plot style "continuous" (default) | "off" | "discontinuous"

FlowData — Data for quiver plot matrix

FlowStyle — Indicator to show quiver plot "arrow" (default) | "off"

XYGrid — Indicator to convert mesh data to x-y grid "off" (default) | "on"

GridParam — Customized x-y grid [tn;a2;a3] from an earlier call to tri2grid

NodeLabels — Node labels "off" (default) | "on"

ElementLabels — Element labels "off" (default) | "on"

Deformation — Data for plotting deformed shape Displacement property of StaticStructuralResults object

DeformationScaleFactor — Scaling factor for plotting deformed shape real number

ColorBar — Indicator to include color bar "on" (default) | "off"

ColorMap — Colormap "cool" (default) | ColorMap value or matrix of such values

Mesh — Indicator to show mesh "off" (default) | "on"

Title — Title of plot string scalar | character vector

FaceAlpha — Surface transparency for 3-D geometry 1 (default) | real number from 0 through 1

Contour — Indicator to plot level curves "off" (default) | "on"

Levels — Levels for contour plot 10 (default) | positive integer | vector of level values

Output Arguments

h — Handles to graphics objects vector

More About

Quiver Plot

Version History

R2021a: Electromagnetic Analysis

R2020a: Improved performance for plots with many text labels

R2018a: Highlighting particular nodes and elements on mesh plots

R2017b: Structural Analysis

R2017a: Thermal Analysis

R2016b: Transparency, node and element labels

See Also

Functions

Live Editor Tasks

Topics

`mesh` — Mesh description
`FEMesh` object

`nodes` — Nodal coordinates
2-by-NumNodes matrix

`elements` — Element connectivity matrix in terms of node IDs
3-by-NumElements matrix | 6-by-NumElements matrix

`model` — Model object
`PDEModel` object | `ThermalModel` object | `StructuralModel` object | `ElectromagneticModel` object

`p` — Mesh points
matrix

`e` — Mesh edges
matrix

`t` — Mesh triangles
matrix

`XYData` — Colored surface plot data
vector

`XYStyle` — Coloring choice
`"interp"` (default) | `"off"` | `"flat"`

`ZData` — Data for 3-D plot heights
matrix

`ZStyle` — 3-D plot style
`"continuous"` (default) | `"off"` | `"discontinuous"`

`FlowData` — Data for quiver plot
matrix

`FlowStyle` — Indicator to show quiver plot
`"arrow"` (default) | `"off"`

`XYGrid` — Indicator to convert mesh data to x-y grid
`"off"` (default) | `"on"`

`GridParam` — Customized x-y grid
`[tn;a2;a3]` from an earlier call to `tri2grid`

`NodeLabels` — Node labels
`"off"` (default) | `"on"`

`ElementLabels` — Element labels
`"off"` (default) | `"on"`

`Deformation` — Data for plotting deformed shape
`Displacement` property of `StaticStructuralResults` object

`DeformationScaleFactor` — Scaling factor for plotting deformed shape
real number

`ColorBar` — Indicator to include color bar
`"on"` (default) | `"off"`

`ColorMap` — Colormap
`"cool"` (default) | `ColorMap` value or matrix of such values

`Mesh` — Indicator to show mesh
`"off"` (default) | `"on"`

`Title` — Title of plot
string scalar | character vector

`FaceAlpha` — Surface transparency for 3-D geometry
`1` (default) | real number from `0` through `1`

`Contour` — Indicator to plot level curves
`"off"` (default) | `"on"`

`Levels` — Levels for contour plot
`10` (default) | positive integer | vector of level values

`h` — Handles to graphics objects
vector