Solve 2-D PDEs Using the PDE Modeler App
To solve 2-D PDE problems using the PDE Modeler app follow these steps:
Start the PDE Modeler app by using the Apps tab or typing
pdeModelerin the MATLAB® Command Window. For details, see Open the PDE Modeler App.Choose the application mode by selecting Application from the Options menu.
Create a 2-D geometry by drawing, rotating, and combining the basic shapes: circles, ellipses, rectangles, and polygons. To draw and rotate shapes, use the Draw menu or the corresponding toolbar buttons. To combine shapes, use the Set formula field. See 2-D Geometry Creation in PDE Modeler App.
Specify boundary conditions for each boundary segment. To do this, first switch to the Boundary Mode by using the Boundary menu. Click the boundary to select it, then specify the boundary condition for that boundary. You can have different types of boundary conditions on different boundary segments. The default boundary condition is the Dirichlet condition hu = r with h = 1 and r = 0. You can remove unnecessary subdomain borders by selecting Remove Subdomain Border or Remove All Subdomain Borders from the Boundary menu. For details, see Specify Boundary Conditions in the PDE Modeler App.
Specify PDE coefficients by selecting PDE Mode from the PDE menu. Then select a region or multiple regions for which you are specifying the coefficients. Select PDE Specification from the PDE menu or click the
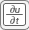 button on the toolbar. Type the coefficients in
the resulting dialog box. For details, see Coefficients for Scalar PDEs
and Coefficients for Systems of PDEs.
button on the toolbar. Type the coefficients in
the resulting dialog box. For details, see Coefficients for Scalar PDEs
and Coefficients for Systems of PDEs.You can specify the coefficients at any time before solving the PDE because the coefficients are independent of the geometry and the boundaries. If the PDE coefficients are material-dependent, specify them by double-clicking each particular region.
Generate a triangular mesh by selecting Initialize Mesh from the Mesh menu. Using the same menu, you can also refine mesh, display node and triangle labels, and control mesh parameters, letting you generate a mesh that is fine enough to adequately resolve the important features in the geometry, but is coarse enough to run in a reasonable amount of time and memory. See Specify Mesh Parameters in the PDE Modeler App.
Solve the PDE by clicking the
 button or by selecting Solve
PDE from the Solve menu. To use a
solver with non-default parameters, select Parameters
from the Solve menu to. The resulting dialog box lets
you:
button or by selecting Solve
PDE from the Solve menu. To use a
solver with non-default parameters, select Parameters
from the Solve menu to. The resulting dialog box lets
you:Invoke and control the nonlinear and adaptive solvers for elliptic problems.
Specify the initial values, and the times for which to generate the output for parabolic and hyperbolic problems.
Specify the interval in which to search for eigenvalues for eigenvalue problems.
When you solve the PDE, the app automatically plots the solution using the default settings. To customize the plot or plot other physical properties calculated using the solution, select Parameters from the Plot menu. See Plot the Solution in the PDE Modeler App.
Tips
After solving the problem, you can:
Export the solution or the mesh or both to the MATLAB workspace for further analysis.
Visualize other properties of the solution.
Change the PDE and recompute the solution.
Change the mesh and recompute the solution. If you select Initialize Mesh, the mesh is initialized; if you select Refine Mesh, the current mesh is refined. From the Mesh menu, you can also jiggle the mesh and undo previous mesh changes. You also can use the adaptive mesh refiner and solver,
adaptmesh. This option tries to find a mesh that fits the solution.Change the boundary conditions. To return to the mode where you can select boundaries, use the ∂Ω button or the Boundary Mode option from the Boundary menu.
Change the geometry. You can switch to the draw mode again by selecting Draw Mode from the Draw menu or by clicking one of the Draw Mode icons to add another shape.
The following are the shortcuts that you can use to skip one or more steps. In general, the PDE Modeler app adds the necessary steps automatically.
If you do not create a geometry, the PDE Modeler app uses an L-shaped geometry with the default boundary conditions.
If you initialize the mesh while in the draw mode, the PDE Modeler app first decomposes the geometry using the current set formula and assigns the default boundary condition to the outer boundaries. After that, it generate the mesh.
If you refine the mesh before initializing it, the PDE Modeler app first initializes the mesh.
If you solve the PDE without generating a mesh, the PDE Modeler app initializes a mesh before solving the PDE.
If you select a plot type and choose to plot the solution, the PDE Modeler app checks if the solution to the current PDE is available. If not, the PDE Modeler app first solves the current PDE. The app displays the solution using the selected plot options.
If do not specify the coefficients and use the default Generic Scalar application mode, the PDE Modeler app solves the default PDE, which is Poisson's equation:
–Δu = 10.
This corresponds to the generic elliptic PDE with c = 1, a = 0, and f = 10. The default PDE settings depend on the application mode.