Health Indicator Designer
Interactively transform a set of features into a single composite health indicator that can be used to predict the remaining useful life (RUL) of a machine
Since R2024a
Description
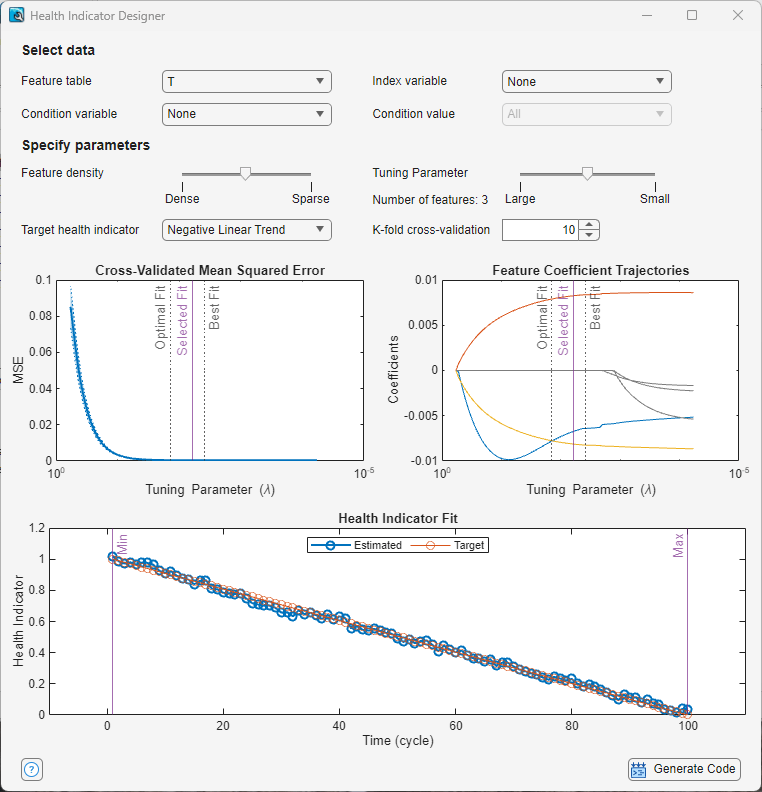
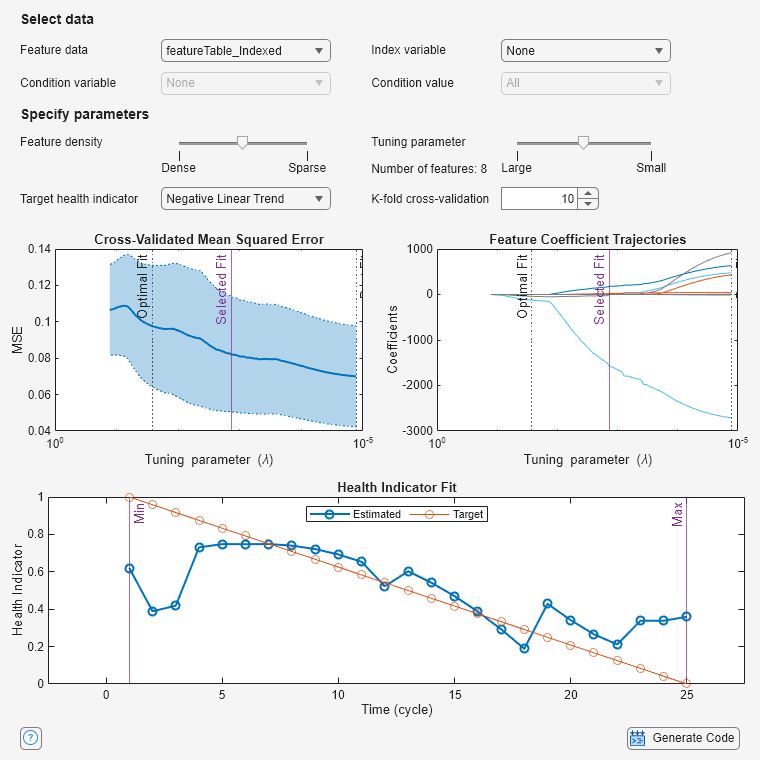
The Health Indicator Designer app allows you to fuse a set of features into a single health indicator (HI) that represents the state of health for the overall system. You can use this single indicator to simplify condition monitoring and RUL predictions in RUL applications.
The app generates MATLAB® code that encapsulates the construction of the HI, which is expressed as a weighted sum, with a weight value for each feature that the HI includes.
H(t) = a0 + a1f1(t) + a2f2(t) + … + anfn(t)
Here, the ai terms are the coefficients that weight the feature contributions. The fi terms are the values of the individual features at time t. a0 is the intercept value. H is typically normalized to a range of [0,1] or [1,0].
To use the app, perform the following general steps.
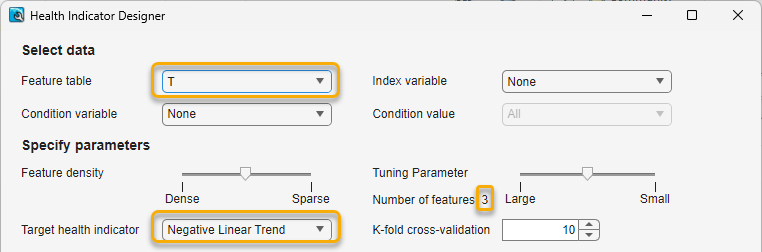
Import feature data that contains an ordered set of features that are extracted from measured or simulated data, such as a feature table you export from Diagnostic Feature Designer.
Specify a target profile that represents the degradation profile that you expect the system to follow.
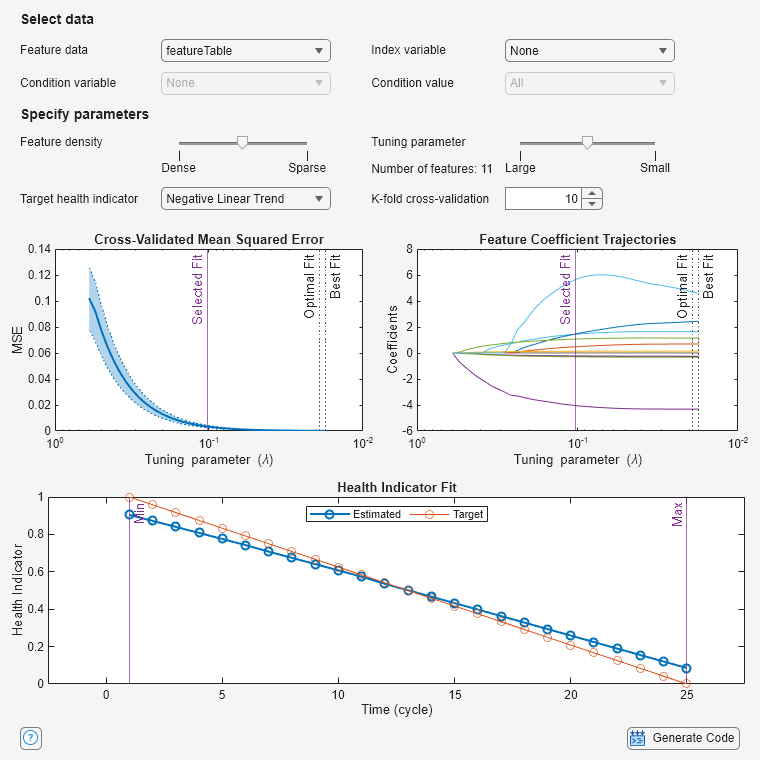
Use the sliders to trade off the number of features in the HI linear model with the mean squared error (MSE) of the fit of the HI to the target profile. The goal is to maintain an acceptable level of MSE while using as few features as possible.
Use the Tuning Parameter slider to tune the MSE. As you move the slider from Large to Small, you reduce the MSE but increase the number of features that the HI includes.
Use the Feature Density slider to distribute the features with respect to the tuning parameter position. Spreading the features out in this way provides finer control over which features the model incorporates. Feature Density is particularly useful for controlling the number of partially correlated features that the HID includes.
For more information on the app options and the plot contents, see the corresponding items in the Parameters section.
For information on the algorithms that the app uses, see Algorithms.
Open the Health Indicator Designer App
MATLAB toolstrip: On the Apps tab, under Control System Design and Analysis, click the app icon.
MATLAB command prompt: Enter
healthIndicatorDesigner.
Examples
Parameters
Programmatic Use
Algorithms
Health Indicator Designer uses the elastic net method, which is related to the lasso algorithm (least absolute shrinkage and selection operator), from the Statistics and Machine Learning Toolbox™ to fit a model to the target. Elastic net regularization is a popular approach for model reduction, as it balances mean squared error and uncertainty.
The parameters and plots that the app displays are products of the lasso processing, which the app configures for the elastic net option. A key
lasso tuning parameter is the regularization parameter λ, which influences
how many predictors or, for Health Indicator Designer, features, to use in the
model. The elastic net algorithm uses both λ and a second parameter,
α, which, for elastic net, is constrained between 0 and 1. Using
α has benefits especially when working with highly correlated predictors.
In the app, the Feature density slider represents
α.
For more information about the lasso and elastic net algorithms, see Lasso and Elastic Net.
References
[1] Zou, Hui, and Trevor Hastie. “Regularization and Variable Selection Via the Elastic Net.” Journal of the Royal Statistical Society Series B: Statistical Methodology, vol. 67, no. 2, Apr. 2005, pp. 301–20.
[2] Moradi, Morteza, et al. “Intelligent Health Indicator Construction for Prognostics of Composite Structures Utilizing a Semi-Supervised Deep Neural Network and SHM Data.” Engineering Applications of Artificial Intelligence, vol. 117, Jan. 2023, p. 105502. DOI.org (Crossref), https://doi.org/10.1016/j.engappai.2022.105502.
Version History
Introduced in R2024a