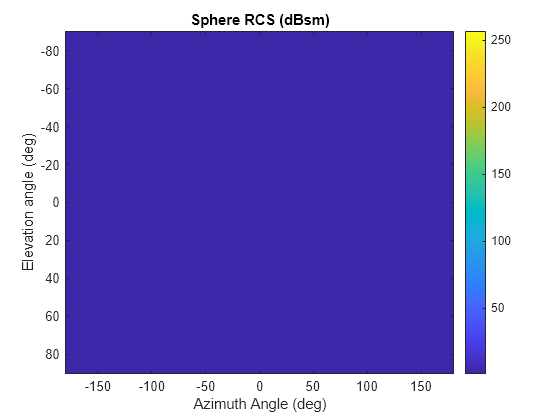
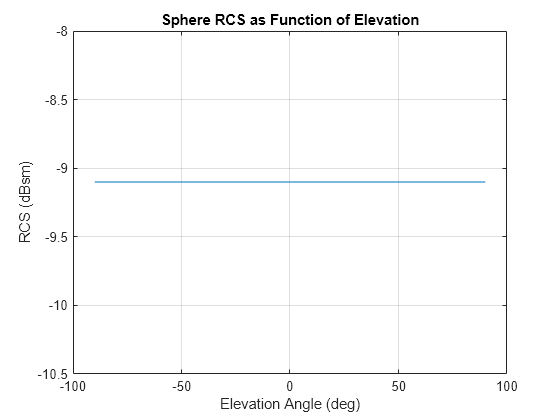
rcssphere
Syntax
Description
Examples
Input Arguments
Output Arguments
More About
References
[1] Mahafza, Bassem. Radar Systems Analysis and Design Using MATLAB, 2nd Ed. Boca Raton, FL: Chapman & Hall/CRC, 2005.
Extended Capabilities
Version History
Introduced in R2021a
See Also
rcscylinder | rcsdisc | rcstruncone | phased.BackscatterRadarTarget | phased.RadarTarget