Water Distribution System Scheduling Using Reinforcement Learning

Fix Random Seed Generator to Improve Reproducibility

The example code may involve computation of random numbers at various stages such as initialization of the agent, creation of the critic, resetting the environment during simulations, generating observations (for stochastic environments), generating exploration actions, and sampling min-batches of experiences for learning. Fixing the random number stream preserves the sequence of the random numbers every time you run the code and improves reproducibility of results. You will fix the random number stream at various locations in the example.

Fix the random number stream with the seed 0 and random number algorithm Mersenne Twister. For more information on random number generation see rng.

previousRngState = rng(0,"twister")

previousRngState = struct with fields:
     Type: 'twister'
     Seed: 0
    State: [625x1 uint32]

The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.

Water Distribution System

The following figure shows a water distribution system.

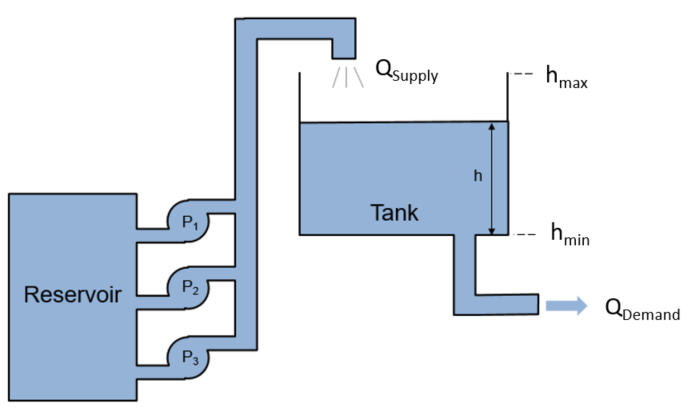
Here:

The objective of the reinforcement learning agent is to schedule the number of pumps running to both minimize the energy usage of the system and satisfy the usage demand ($\mathit{h}>0$). The dynamics of the tank system are governed by the following equation.

Here, $\mathit{A}=40{\mathit{m}}^2$ and ${\mathit{h}}_{\max }=7\mathit{m}$. The demand over a 24 hour period is a function of time given as

where $\mu \left(\mathit{t}\right)$is the expected demand and $\eta \left(\mathit{t}\right)$ represents the demand uncertainty, which is sampled from a uniform random distribution.

The supply is determined by the number of pumps running, $\mathit{a}\in \left\{0,1,2,3\right\}$according to the following mapping.

To simplify the problem, power consumption is defined as the number of pumps running, $\mathit{a}$.

The following function is the reward for this environment. To avoid overflowing or emptying the tank, an additional cost is added if the water height is close to the maximum or minimum water levels, ${\mathit{h}}_{\max }$or ${\mathit{h}}_{\min }$, respectively.

Generate Demand Profile

To generate and a water demand profile based on the number of days considered, use generateWaterDemand defined at the end of this example.

num_days = 4; % Number of days
[WaterDemand,T_max] = generateWaterDemand(num_days);

View the demand profile.

plot(WaterDemand)

Open and Configure Model

Open the distribution system Simulink® model.

mdl = "watertankscheduling";
open_system(mdl)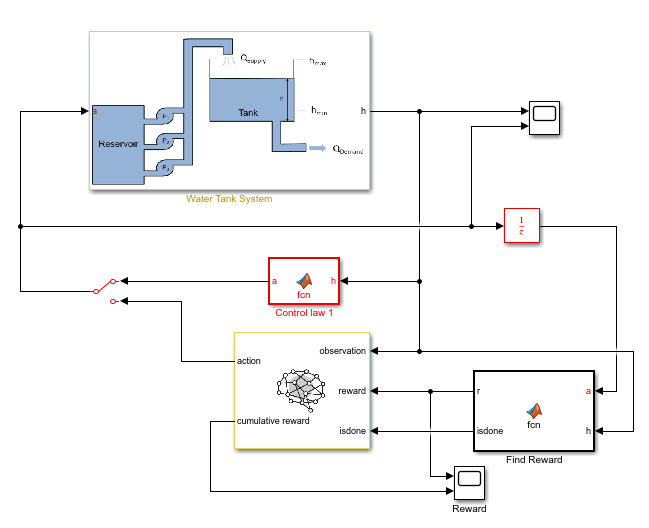

In addition to the reinforcement learning agent, a simple baseline controller is defined in the Control law MATLAB Function block. This controller activates a certain number of pumps depending on the water level.

Specify the initial water height.

h0 = 3; % m

Specify the model parameters.

SampleTime = 0.2;
H_max = 7; % Max tank height (m)
A_tank = 40; % Area of tank (m^2)

Create Environment Object

To create an environment interface for the Simulink model, first define the action and observation specifications, actInfo and obsInfo, respectively. The agent action is the selected number of pumps. The agent observation is the water height, which is measured as a continuous-time signal.

actInfo = rlFiniteSetSpec([0,1,2,3]);
obsInfo = rlNumericSpec([1,1]);

Create the environment interface.

env = rlSimulinkEnv(mdl,mdl+"/RL Agent",obsInfo,actInfo);

Initialize the random seed for each simulation.

simulationSeed(0);

Specify the custom reset function localResetFcn, which is defined at the end of this example, that randomizes the initial water height and the water demand. Doing so allows the agent to be trained on different initial water levels and water demand functions for each episode.

env.ResetFcn = @localResetFcn;

Create DQN Agent

DQN agents use a parametrized Q-value function approximator to estimate the value of the policy. Since DQN agents have a discrete action space, you have the option to create a vector (that is multi-output) Q-value function critic, which is generally more efficient than a comparable single-output critic.

A vector Q-value function takes only the observation as input and returns as output a single vector with as many elements as the number of possible actions. The value of each output element represents the expected discounted cumulative long-term reward when an agent starts from the state corresponding to the given observation and executes the action corresponding to the element number (and follows a given policy afterwards).

The network parameters are initialized randomly. Ensure reproducibility by fixing the seed of the random generator.

rng(0,"twister");

To model the parametrized Q-value function within the critic, use a non-recurrent neural network.

layers = [
    featureInputLayer(obsInfo.Dimension(1))
    fullyConnectedLayer(32)
    reluLayer
    fullyConnectedLayer(32)
    reluLayer
    fullyConnectedLayer(32)
    reluLayer
    fullyConnectedLayer(numel(actInfo.Elements))
    ];

Create to a dlnetwork object and display the number of parameters.

dnn = dlnetwork(layers);
summary(dnn)

   Initialized: true

   Number of learnables: 2.3k

   Inputs:
      1   'input'   1 features

Create a critic using rlVectorQValueFunction using the defined deep neural network and the environment specifications.

critic = rlVectorQValueFunction(dnn,obsInfo,actInfo);

Create DQN Agent With Custom Network

Specify training options for the critic and the actor using rlOptimizerOptions.

criticOpts = rlOptimizerOptions(LearnRate=1e-2,GradientThreshold=10);

Specify the agent options using rlDQNAgentOptions. If you are using an LSTM network, set the sequence length to 20.

opt = rlDQNAgentOptions(SampleTime=SampleTime); 
opt.DiscountFactor = 0.995;
opt.ExperienceBufferLength = 1e6;
opt.EpsilonGreedyExploration.EpsilonDecay = 1e-5;
opt.EpsilonGreedyExploration.EpsilonMin = .02;
opt.MiniBatchSize = 128;
opt.TargetSmoothFactor = 1e-2;

Include the training options for the critic.

opt.CriticOptimizerOptions = criticOpts;

Create the agent using the critic and the options object.

agent = rlDQNAgent(critic,opt);    

Train Agent

To train the agent, first specify the training options. For this example, use the following options.

Specify the options for training using an rlTrainingOptions object.

trainOpts = rlTrainingOptions(...
    MaxEpisodes=500, ...
    MaxStepsPerEpisode=ceil(T_max/SampleTime), ...
    Verbose=false, ...
    Plots="training-progress",...
    StopTrainingCriteria="none",...
    ScoreAveragingWindowLength=100);

Fix the random stream for reproducibility.

rng(0,"twister");

Train the agent using the train function. Training this agent is a computationally intensive process that takes several hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

doTraining = false;
if doTraining

    % Connect the RL Agent block by toggling 
    % the Manual Switch block
    set_param(mdl+"/Manual Switch","sw","0");

    % Train the agent.
    trainingStats = train(agent,env,trainOpts);
else
    % Load the pretrained agent for the example.
    load("SimulinkWaterDistributionDQN.mat","agent")
end

The following figure shows the training progress.

Simulate DQN Agent

To validate the performance of the trained agent, simulate it in the water-tank environment. For more information on agent simulation, see rlSimulationOptions and sim.

To simulate the agent performance, connect the RL Agent block by toggling the manual switch block.

set_param(mdl+"/Manual Switch","sw","0");

Set the maximum number of steps for each simulation and the number of simulations. For this example, run 30 simulations. The environment reset function sets a different initial water height and water demand are different in each simulation.

NumSimulations = 30;
simOptions = rlSimulationOptions( ...
    MaxSteps=T_max/SampleTime,...
    NumSimulations=NumSimulations);

To compare the agent with the baseline controller under the same conditions, reset the initial random seed used in the environment reset function.

simulationSeed(0);

Simulate the agent against the environment.

experienceDQN = sim(env,agent,simOptions);

Simulate Baseline Controller

To compare DQN agent with the baseline controller, you must simulate the baseline controller using the same simulation options and initial random seed for the reset function.

Enable the baseline controller.

set_param(mdl+"/Manual Switch","sw","1");

To compare the agent with the baseline controller under the same conditions, reset the random seed used in the environment reset function.

simulationSeed(0);

Simulate the baseline controller against the environment.

experienceBaseline = sim(env,agent,simOptions);

Compare DQN Agent with Baseline Controller

Initialize cumulative reward result vectors for both the agent and baseline controller.

resultVectorDQN = zeros(NumSimulations, 1);
resultVectorBaseline = zeros(NumSimulations,1);

Calculate cumulative rewards for both the agent and the baseline controller.

for ct = 1:NumSimulations
    resultVectorDQN(ct) = sum(experienceDQN(ct).Reward);
    resultVectorBaseline(ct) = sum(experienceBaseline(ct).Reward);
end

Plot the cumulative rewards.

plot([resultVectorDQN resultVectorBaseline],"o")
set(gca,"xtick",1:NumSimulations)
xlabel("Simulation number")
ylabel("Cumulative Reward")
legend("DQN","Baseline","Location","NorthEastOutside")

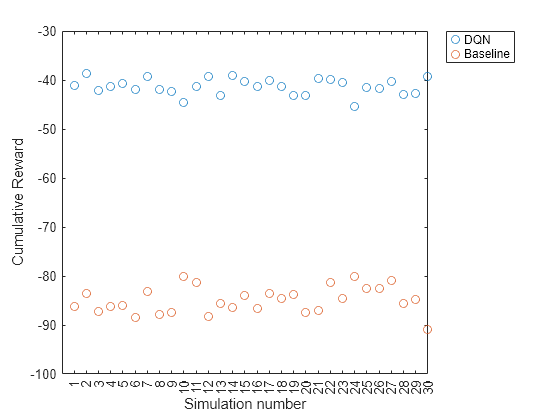
The cumulative reward obtained by the agent is consistently around –40. This value is much greater than the average reward obtained by the baseline controller. Therefore, the DQN agent consistently outperforms the baseline controller in terms of energy savings.

Restore the random number stream using the information stored in previousRngState.

rng(previousRngState);

Local Functions

Water Demand Function

function [WaterDemand,T_max] = generateWaterDemand(num_days)

    t = 0:(num_days*24)-1; % hr
    T_max = t(end);

    Demand_mean = [28, 28, 28, 45, 55, 110, ...
                   280, 450, 310, 170, 160, 145, ... 
                   130, 150, 165, 155, 170, 265, ...
                   360, 240, 120, 83, 45, 28 ]'; % m^3/hr

    Demand = repmat(Demand_mean,1,num_days);
    Demand = Demand(:);

    % Add noise to demand
    a = -25; % m^3/hr
    b = 25; % m^3/hr
    Demand_noise = a + (b-a).*rand(numel(Demand),1);

    WaterDemand = timeseries(Demand + Demand_noise,t);
    WaterDemand.Name = "Water Demand";
    WaterDemand.TimeInfo.Units = "hours";
end

Reset Function

function in = localResetFcn(in)

    % Use a persistent random seed value to evaluate the agent 
    % and the baseline controller under the same conditions.

    randomSeed = simulationSeed(simulationSeed() + 1);
    rng(randomSeed);
    
    % Randomize water demand.
    num_days = 4;
    H_max = 7;
    [WaterDemand,~] = generateWaterDemand(num_days);
    assignin("base","WaterDemand",WaterDemand)

    % Randomize initial height.
    h0 = 3*randn;
    while h0 <= 0 || h0 >= H_max
        h0 = 3*randn;
    end

    blk = "watertankscheduling/Water Tank System/Initial Water Height";
    in = setBlockParameter(in,blk,"Value",num2str(h0));

end
function s = simulationSeed(u)
    persistent x;
    if isempty(x)
        x = 0;
    end
    if nargin
        x = u;
    end
    s = x;
end