Main Content

rf.Mixer

Model RF and IQ modulator and RF and IQ demodulator with impairments and noise

Since R2024b

expand all in page

Description

Use the rf.Mixer System object™ to create an idealized mixer for command line simulation. The rf.Mixer System object models four complex baseband mixers with impairments and noise. The four mixer types that this System object models are modulator, demodulator, IQ modulator, and IQ demodulator. You can also add impairments, include IQ gain, and phase mismatch where appropriate, while noise includes both system and LO phase noise to the mixer element.

To create an idealized mixer to process complex signals:

  1. Create the rf.Mixer object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

rfmix = rf.Mixer
rfmix = rf.Mixer(Name=Value)

Description

rfmix = rf.Mixer creates an idealized mixer that allows you to process complex signals with noise and nonlinearities.

example

rfmix = rf.Mixer(Name=Value) sets properties of the rf.Mixer object using one or more name-value arguments. For example, rfmix = rf.Mixer(Model='iqmod') creates an idealized IQ modulator element. Properties you do not specify retain their default values.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Main

Type of mixer, specified as one of the following:

  • mod — Modulator

  • demod — Demodulator

  • iqmod — IQ Modulator

  • iqdemod — IQ Demodulator

For more information, see Mixer Architectures and Design Equations (RF Blockset).

Sidebands of the mixer, specified as upper or lower.

For more information, see Mixer Sidebands (RF Blockset).

Dependencies

To enable this property, set Sideband to mod.

Conversion gain for the mixer model, specified as a real number in dB.

RF carrier frequency for the mixer model, specified as a positive real number in Hz.

Local oscillator frequency for the mixer model, specified as a positive real number in Hz.

Impairments

LO phase offset, specified as a real number in degrees.

Dependencies

To enable this property, set Model to mod or demod.

IQ gain imbalance, specified as a nonnegative real number in dB.

Dependencies

To enable this property, set Model to iqmod or iqdemod.

IQ phase imbalance, specified as a real number in degrees.

Dependencies

To enable this property, set Model to iqmod or iqdemod.

Type of third-order nonlinearity type in the cubic polynomial model, specified as IIP3, OIP3, IP1dB, OP1dB, IPsat, or OPsat.

For more information, see Nonlinearities in Idealized Baseband Mixer Block (RF Blockset).

Input third-order intercept point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Nonlinearity to IIP3.

Output third-order intercept point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Nonlinearity to OIP3.

Input 1 dB compression point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Nonlinearity to IP1dB.

Output 1 dB compression point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Nonlinearity to OP1dB.

Input saturation point, specified as a real positive number in dBm.

Dependencies

To enable this property, set Nonlinearity to IPsat.

Output saturation point, specified as a positive real number in dBm.

Dependencies

To enable this property, set Nonlinearity to OPsat.

Mixer Noise

Options to add mixer noise to the system, specified as logical 1(true) or 0 (false).

For more information, see Mixer (System) Noise Simulations (RF Blockset).

Type of noise, specified as a noise-temperature, NF, or noise-factor.

For more information, see Mixer (System) Noise Simulations (RF Blockset).

Dependencies

To enable this property, set IncludeNoise to 1 or true.

Noise temperature to model the mixer noise, specified as a nonnegative real number in kelvin.

Dependencies

To enable this property, set IncludeNoiseto 1 or true and set NoiseType to noise-temperature.

Noise figure to model the mixer noise, specified as a nonnegative real number in dB.

Dependencies

To enable this property, set IncludeNoiseto 1 or true and set NoiseType to NF.

Noise factor to model mixer noise, specified as a positive integer scalar greater than or equal to 1.

Dependencies

To enable this property, set IncludeNoise to 1 or true and set NoiseType to noise-factor.

Source of initial seed used to prepare the Gaussian random number noise generator, specified as one of the following:

  • auto — When you set NoiseSeedSource to auto, the object generates seeds for each mixer instance using a random number generator. The reset method of the instance has no effect.

  • user — When you set NoiseSeedSource to user, the object uses the value you provide in the NoiseSeed property to initialize the random number generator. The reset method resets the random number generator using the NoiseSeed property value.

Dependencies

To enable this property, set IncludeNoise to 1 or true.

Seed for the random number generator, specified as a nonnegative integer less than 232. Use this value to initialize the random number generator.

Dependencies

To enable this property, set IncludeNoise to 1 or true and NoiseSeedSource to user.

Phase Noise

Add LO phase noise to LO signal, specified as a logical 0 (false) or 1 (true).

For more information, see Phase Noise in Mixer Block (RF Blockset).

Phase noise level relative to carrier, specified as negative real scalar or vector in dBc/Hz.

Note

The number of terms specified in the PhaseNoiseLevel property must equal the number of terms in the PhaseNoiseFrequencyOffset property.

Dependencies

To enable this property, set IncludePhaseNoise to 1 or true.

Data Types: double

Phase frequency offset, specified as a positive real scalar or vector of positive increasing real scalar of type double in Hz.

Note

The number of terms specified in the PhaseNoiseFrequencyOffset property must equal the number of terms in the PhaseNoiseLevel property.

Dependencies

To enable this property, set IncludePhaseNoise to 1 or true.

Options to automatically determine number of frequency bins used in a two-sided phase noise spectrum, specified as a logical 0 (false) or 1 (true).

You can also set the number of frequency bins using the PhaseNoiseNumSamples and SampleRate properties when you set the PhaseNoiseNumSamples property is set to off.

Dependencies

To enable this property, set IncludePhaseNoise to 1 or true.

Number of samples in the time-domain signal, specified as a real nonnegative integer less than or equal to 65536.

The value you specify here can also represent the number of frequency lines (bins) in the signal's two-sided frequency spectrum required to achieve the frequency resolution for the frequency offset specified in the PhaseNoiseFrequencyOffset property.

The distance between frequency lines is SampleRate/PhaseNoiseNumSamples. For non-positive values, the object estimates PhaseNoiseNumSamples using the values of the PhaseNoiseLevel and PhaseNoiseFrequencyOffset properties. Frequency resolution increases as the number of signal samples increases.

Note

You must set the value of this parameter to a power of 2.

Dependencies

To enable this parameter, set the IncludePhaseNoise to 1 or true parameter and set PhaseNoiseNumSamples to 0 (false).

Source of initial seed used to prepare the Gaussian random number LO phase noise generator, specified as one of the following:

  • auto — When you set the PhaseNoiseSeedSource to auto, the object generates seeds for each mixer instance using a random number generator. The reset method of the instance has no effect.

  • user — When you set the PhaseNoiseSeedSource to user, the object uses the value you provide in the PhaseNoiseSeed property to initialize the random number generator. The reset method resets the random number generator using the PhaseNoiseSeed property value.

Dependencies

To enable this property, set IncludePhaseNoise to 1 or true.

Seed for the random number generator, specified as a nonnegative integer less than 232. Use this value to initialize the random number generator.

Dependencies

To enable this property, set IncludePhaseNoise to 1 or true and PhaseNoiseSeedSource to user.

Sample rate, specified as a nonnegative real scalar of data type double in samples per second.

Dependencies

To enable this property, set IncludePhaseNoise to 1 or true.

Usage

Syntax

out = rfmix(in)

Description

out = rfmix(in) returns a time-dependent output signal out based on the time-dependent input signal in.

example

Input Arguments

expand all

Time-dependent input signal, specified as a real scalar, real column, complex scalar, or complex column. A column represents consecutive points in time.

Data Types: double | single

Output Arguments

expand all

Time-dependent output signal, returned as a complex scalar or complex column. The output time-dependent signal is equal in size to the input time-dependent signal.

Data Types: double | single

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

visualizePowerPlot power characteristics of idealized mixer
visualizePhaseNoisePlot phase noise characteristics of idealized mixer
stepRun System object algorithm
releaseRelease resources and allow changes to System object property values and input characteristics
resetReset internal states of System object

Examples

collapse all

This example uses:

Open Live Script

Create an rf.Mixer System object.

rfmix = rf.Mixer('Nonlinearity','IPsat','IPsat',30);

Generate a 16 QAM signal.

in = qammod(randi([0 15],1000,1),16,'UnitAveragePower',true);

Apply the cubic nonlinearity mixer model to the16 QAM signal and plot the results. 

out = rfmix(in);
scatterplot(out)

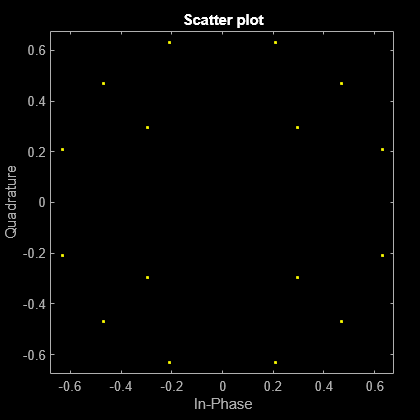
Figure Scatter Plot contains an axes object. The axes object with title Scatter plot, xlabel In-Phase, ylabel Quadrature contains a line object which displays its values using only markers. This object represents Channel 1.

Open Live Script

Define modulation order, samples per symbol, and input power.

M = 16;       
sps = 4;       
pindBm = 0;

Create an idealized baseband mixer element with the phase offset of 2 degrees.

  rfMixer = rf.Mixer('PhaseOffset',2);

Apply pulse shaping by interpolating an input signal using a raised cosine finite impulse response (FIR) filter.

txfilter = comm.RaisedCosineTransmitFilter('RolloffFactor',0.9, 'FilterSpanInSymbols',6, ...
      'OutputSamplesPerSymbol',sps,'Gain',sqrt(sps));

Define the input signal.

pin = 10.^((pindBm-30)/10);     % Unit: W
data = randi([0 M-1],1000,1);

Define the modulated, filtered, and mixer signals.

modSignal = qammod(data,M,'UnitAveragePower',true)*sqrt(pin);
filterSignal = txfilter(modSignal);
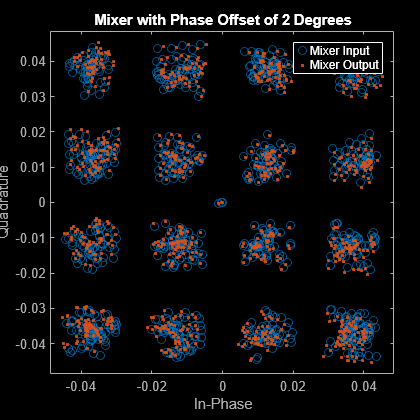
mixerSignal = rfMixer(filterSignal);

Plot the mixer characteristics with a phase offset of 2 degrees.

scatFig = scatterplot(filterSignal,sps,0,'o');
hold on
scatterplot(mixerSignal,sps,0,'.',scatFig)
legend({'Mixer Input' 'Mixer Output'},'Location','northeast')
title('Mixer with Phase Offset of 2 Degrees')

Figure Scatter Plot contains an axes object. The axes object with title Mixer with Phase Offset of 2 Degrees, xlabel In-Phase, ylabel Quadrature contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Mixer Input, Mixer Output.

This example uses:

Open Live Script

This example shows how to input a two-tone signal to an idealized system. To design this RF system:

  • First, generate a two-tone source.

  • Second, connect this two-tone source to an idealized RF PA.

  • Finally, observe the output response of this system.

Introduction

The RF system designed in this example uses the Idealized Baseband System object™ to analyze a cascade of mathematical models of RF components within the MATLAB® environment. During analysis, these System objects uses complex-baseband representation of the RF elements to compute time-domain waveforms. These complex modulated signals represent the transmitted information, assumed to be centered around an implicit carrier frequency. The models from the Idealized Baseband library do not model out-of-band behavior or spurious harmonics generated by nonlinear effects or interfering signals. Additionally, models from the Idealized Baseband library do not model impedance mismatches and assume that all blocks are perfectly matched. As a result, RF models built with the Idealized Baseband library simulate rapidly.

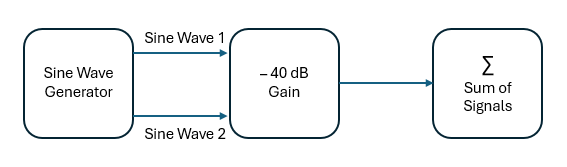
Create Two-Tone Source Generator

This figure shows the architecture of a two-tone source generator. This generator consists of a sine wave generator that produces two sinusoidal signals. These signals are multiplied by a -40 dB gain and then processed by a summer.

signalgen.png

Define sample rate and samples per frame of the sine wave signals.

sampleRate = 1/2e-8;
samplesPerFrame = 512;

Define a gain of - 40 dB.

m40dB = 10^(-40/20); % Request Jeff: Why -40 dB?

Create two sinusoid signals at 1.8 GHz and 2.6 GHz.

SineObj1 = dsp.SineWave('Frequency',1.8e6,'SampleRate',sampleRate,      ...
    SamplesPerFrame=samplesPerFrame,ComplexOutput=true);
SineObj2 = dsp.SineWave('Frequency',2.6e6,'SampleRate',sampleRate,      ...
    SamplesPerFrame=samplesPerFrame,ComplexOutput=true);

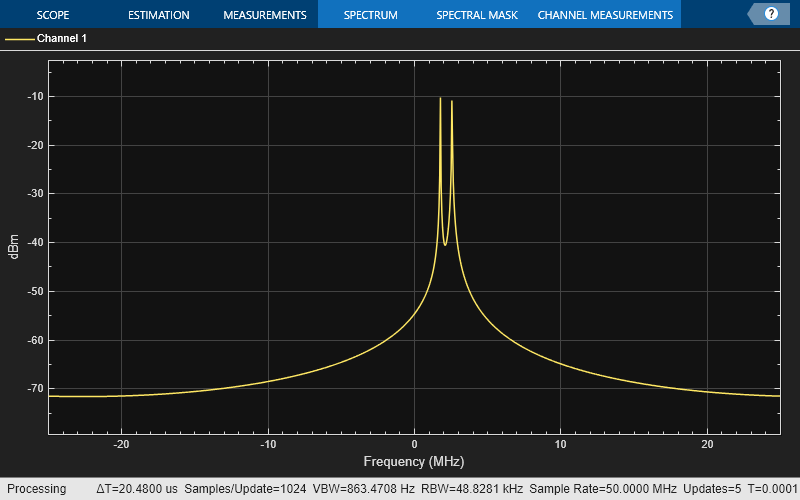
Display the spectral analysis of a two tone signal source, where each tone is -10 dBm.

SpectAnal = spectrumAnalyzer('SampleRate',sampleRate,'ShowLegend',true);

for Iter = 1:10
    sineWave1 = SineObj1();
    sineWave2 = SineObj2();
    sigIn = m40dB*(sineWave1 + sineWave2);
    SpectAnal(sigIn);
end

Simulate Idealized System

This figure shows how to create a system to IQ modulate the two-tone signal and amplify using an RF PA. The system architecture involves connecting a cubic polynomial amplifier to an IQ modulator. The output from the IQ modulator is then connected to a cross-term (CT) memory power amplifier. A two-tone signal is supplied as input to the system, and the output is connected to a spectrum analyzer for visualizing the power amplifier characteristics.

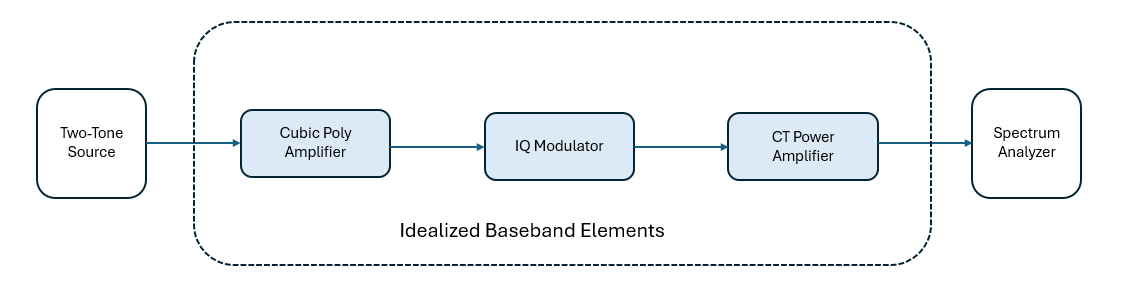
twotonesystem.png

Load the pre-computed PA coefficient matrix.

load('PAcoefficients_rf.mat','fitCoefMat')

Create an idealized baseband cubic polynomial amplifier and IQ modulator with nonlinearity and noise.

preAmpIQ = rf.Amplifier('Gain',8,'Nonlinearity','IIP3','IIP3',45,       ...
    'IncludeNoise',true,NF=1.5);
mixerModIQ = rf.Mixer('Model','iqmod','Gain',0,'LO',1e8,                ...
    'PhaseImbalance',.5,'Nonlinearity','IIP3',IIP3=50,                  ...
    IncludeNoise=true,NoiseType='NF',NF=6);

Create an idealized baseband cross-term memory PA. 

powerAmp = rf.PAmemory('Model','Cross-term memory',                     ...
    'CoefficientMatrix','fitCoefMat');

Connect the RF chain and provide the two-tone signal as input. 

SpectAnal = spectrumAnalyzer('SampleRate',sampleRate,'ShowLegend',true);

for Iter = 1:10
    sineWave1 = SineObj1();
    sineWave2 = SineObj2();
    sineIn = m40dB*(sineWave1 + sineWave2);
    ampIQ = preAmpIQ(sineIn);
    modIQ = mixerModIQ(ampIQ);
    paOut = powerAmp(modIQ*sqrt(50))/sqrt(50);

    SpectAnal(paOut);
end

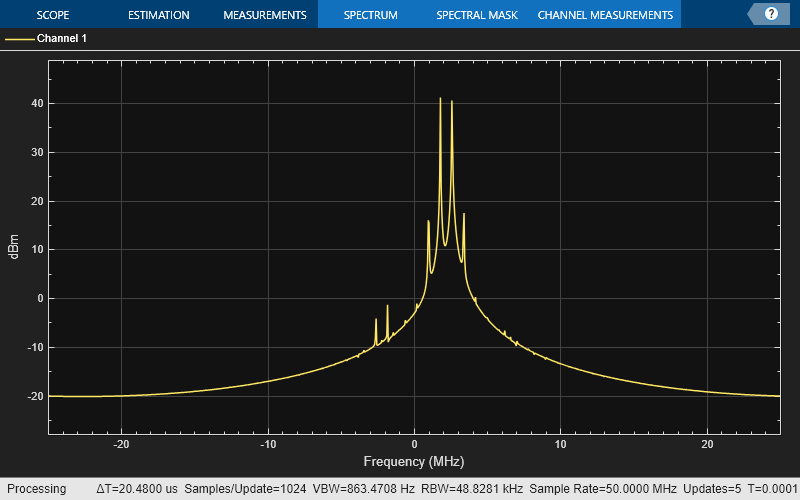
References

[1] Razavi, Behzad. “Basic Concepts “ in RF Microelectronics, 2nd edition, Prentice Hall, 2012.

[2] Kundert, Ken.“ Accurate and Rapid Measurement of IP2 and IP3,“ The Designer Guide Community, May 22, 2002.

[3] Kasdin, N.J. “Discrete Simulation of Colored Noise and Stochastic Processes and 1/f α Power Law Noise Generation.” Proceedings of the IEEE 83, no. 5 (May 1995): 802–27. https://doi.org/10.1109/5.381848.

Version History

Introduced in R2024b

See Also

Blocks