Main Content

modelCalibration

Compute R-square, RMSE, correlation, and sample mean error of predicted and observed EADs

Since R2023a

collapse all in page

Syntax

CalMeasure = modelCalibration(eadModel,data)
[CalMeasure,CalData] = modelCalibration(___,Name=Value)

Description

CalMeasure = modelCalibration(eadModel,data) computes the R-square, root mean square error (RMSE), correlation, and sample mean error of observed vs. predicted exposure at default (EAD) data. modelCalibration supports comparison against a reference model and also supports different correlation types. By default, modelCalibration computes the metrics in the EAD scale. You can use the ModelLevel name-value argument to compute metrics using the underlying model's transformed scale.

example

[CalMeasure,CalData] = modelCalibration(___,Name=Value) specifies options using one or more name-value arguments in addition to the input arguments in the previous syntax.

example

Examples

collapse all

Open Live Script

This example shows how to use fitEADModel to create a Tobit model and then use modelCalibration to compute the R-Square, RMSE, correlation, and sample mean error of predicted and observed EAD.

Load EAD Data

Load the EAD data. 

load EADData.mat
head(EADData)
    UtilizationRate    Age     Marriage        Limit         Drawn          EAD    
    _______________    ___    ___________    __________    __________    __________

        0.24359        25     not married         44776         10907         44740
        0.96946        44     not married    2.1405e+05    2.0751e+05         40678
              0        40     married        1.6581e+05             0    1.6567e+05
        0.53242        38     not married    1.7375e+05         92506        1593.5
         0.2583        30     not married         26258        6782.5        54.175
        0.17039        54     married        1.7357e+05         29575        576.69
        0.18586        27     not married         19590          3641        998.49
        0.85372        42     not married    2.0712e+05    1.7682e+05    1.6454e+05

rng('default');
NumObs = height(EADData);
c = cvpartition(NumObs,'HoldOut',0.4);
TrainingInd = training(c);
TestInd = test(c);

Select Model Type

Select a model type for Tobit or Regression.

ModelType = "Tobit";

Select Conversion Measure

Select a conversion measure for the EAD response values.

ConversionMeasure = "LCF";

Create Tobit EAD Model

Use fitEADModel to create a Tobit model using EADData.

eadModel = fitEADModel(EADData(TrainingInd,:),ModelType,PredictorVars={'UtilizationRate','Age','Marriage'}, ...
    ConversionMeasure=ConversionMeasure,DrawnVar="Drawn",LimitVar="Limit",ResponseVar="EAD");
disp(eadModel);
  Tobit with properties:

        CensoringSide: "both"
            LeftLimit: 0
           RightLimit: 1
              ModelID: "Tobit"
          Description: ""
      UnderlyingModel: [1x1 risk.internal.credit.TobitModel]
        PredictorVars: ["UtilizationRate"    "Age"    "Marriage"]
          ResponseVar: "EAD"
             LimitVar: "Limit"
             DrawnVar: "Drawn"
    ConversionMeasure: "lcf"

Display the underlying model. The underlying model's response variable is the transformation of the EAD response data. Use the 'LimitVar' and 'DrwanVar' name-value arguments to modify the transformation.

disp(eadModel.UnderlyingModel);
Tobit regression model:
     EAD_lcf = max(0,min(Y*,1))
     Y* ~ 1 + UtilizationRate + Age + Marriage

Estimated coefficients:
                             Estimate         SE         tStat        pValue  
                            __________    __________    ________    __________

    (Intercept)                0.22467      0.031085      7.2276    6.4149e-13
    UtilizationRate             0.4714      0.020682      22.793             0
    Age                     -0.0014209    0.00075844     -1.8735      0.061111
    Marriage_not married     -0.010543      0.015817    -0.66654       0.50512
    (Sigma)                     0.3618     0.0049991      72.374             0

Number of observations: 2627
Number of left-censored observations: 0
Number of uncensored observations: 2626
Number of right-censored observations: 1
Log-likelihood: -1057.9

Predict EAD

EAD prediction operates on the underlying compact statistical model and then transforms the predicted values back to the EAD scale. You can specify the predict function with different options for the 'ModelLevel' name-value argument.

predictedEAD = predict(eadModel,EADData(TestInd,:),ModelLevel="ead");
predictedConversion = predict(eadModel,EADData(TestInd,:),ModelLevel="ConversionMeasure");

Validate EAD Model

For model validation, use modelDiscrimination, modelDiscriminationPlot, modelCalibration, and modelCalibrationPlot.

Use modelDiscrimination and then modelDiscriminationPlot to plot the ROC curve.

ModelLevel = "ead";

[DiscMeasure1,DiscData1] = modelDiscrimination(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel);
modelDiscriminationPlot(eadModel,EADData(TestInd, :),ModelLevel=ModelLevel,SegmentBy="Marriage");

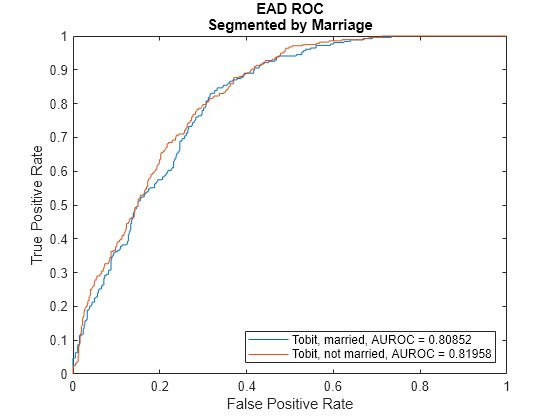
Figure contains an axes object. The axes object with title EAD ROC Segmented by Marriage, xlabel False Positive Rate, ylabel True Positive Rate contains 2 objects of type line. These objects represent Tobit, married, AUROC = 0.80852, Tobit, not married, AUROC = 0.81958.

Use modelCalibration, and modelCalibrationPlot to show a scatter plot of the predictions.

YData = "Observed";

[CalMeasure1,CalData1] = modelCalibration(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel)
CalMeasure1=1×4 table
             RSquared    RMSE     Correlation    SampleMeanError
             ________    _____    ___________    _______________

    Tobit     0.3919     42494      0.62602          -1240.7    


CalData1=1751×3 table
     Observed     Predicted_Tobit    Residuals_Tobit
    __________    _______________    _______________

         44740           14893              29847   
        54.175          8730.2              -8676   
        987.39           13244             -12257   
        9606.4          7367.5             2238.9   
        83.809           27501             -27417   
         73538           45726              27812   
        96.949          5522.5            -5425.5   
        873.21          4426.3            -3553.1   
        328.35          5952.4            -5624.1   
         55237           28040              27198   
         30359           19047              11312   
         39211           28368              10843   
    2.0885e+05      1.0539e+05         1.0346e+05   
        1921.7           19939             -18017   
         15230          5427.4             9802.4   
         20063          9359.6              10703   
      ⋮


modelCalibrationPlot(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel,YData=YData);

Figure contains an axes object. The axes object with title Scatter Tobit, R-Squared: 0.3919, xlabel EAD Predicted, ylabel EAD Observed contains 2 objects of type scatter, line. These objects represent Data, Fit.

Open Live Script

This example shows how to use fitEADModel to create a Beta model and then use modelCalibration to compute the R-Square, RMSE, correlation, and sample mean error of predicted and observed EAD.

Load EAD Data

Load the EAD data. 

load EADData.mat
head(EADData)
    UtilizationRate    Age     Marriage        Limit         Drawn          EAD    
    _______________    ___    ___________    __________    __________    __________

        0.24359        25     not married         44776         10907         44740
        0.96946        44     not married    2.1405e+05    2.0751e+05         40678
              0        40     married        1.6581e+05             0    1.6567e+05
        0.53242        38     not married    1.7375e+05         92506        1593.5
         0.2583        30     not married         26258        6782.5        54.175
        0.17039        54     married        1.7357e+05         29575        576.69
        0.18586        27     not married         19590          3641        998.49
        0.85372        42     not married    2.0712e+05    1.7682e+05    1.6454e+05

rng('default');
NumObs = height(EADData);
c = cvpartition(NumObs,'HoldOut',0.4);
TrainingInd = training(c);
TestInd = test(c);

Select Model Type

Select a model type for Beta.

ModelType = "Beta";

Select Conversion Measure

Select a conversion measure for the EAD response values.

ConversionMeasure = "LCF";

Create Beta EAD Model

Use fitEADModel to create a Beta model using the TrainingInd data.

eadModel = fitEADModel(EADData(TrainingInd,:),ModelType,PredictorVars={'UtilizationRate','Age','Marriage'}, ...
    ConversionMeasure=ConversionMeasure,DrawnVar="Drawn",LimitVar="Limit",ResponseVar="EAD");
disp(eadModel);
  Beta with properties:

    BoundaryTolerance: 1.0000e-07
              ModelID: "Beta"
          Description: ""
      UnderlyingModel: [1x1 risk.internal.credit.BetaModel]
        PredictorVars: ["UtilizationRate"    "Age"    "Marriage"]
          ResponseVar: "EAD"
             LimitVar: "Limit"
             DrawnVar: "Drawn"
    ConversionMeasure: "lcf"

Display the underlying model. The underlying model's response variable is the transformation of the EAD response data. Use the 'LimitVar' and 'DrwanVar' name-value arguments to modify the transformation.

disp(eadModel.UnderlyingModel);
Beta regression model:
     logit(EAD_lcf) ~ 1_mu + UtilizationRate_mu + Age_mu + Marriage_mu
     log(EAD_lcf) ~ 1_phi + UtilizationRate_phi + Age_phi + Marriage_phi

Estimated coefficients:
                                Estimate        SE         tStat        pValue  
                                _________    _________    ________    __________

    (Intercept)_mu               -0.65566      0.11484     -5.7093    1.2614e-08
    UtilizationRate_mu             1.7014     0.078094      21.787             0
    Age_mu                       -0.00559    0.0027603     -2.0252      0.042952
    Marriage_not married_mu     -0.012576     0.052098     -0.2414       0.80926
    (Intercept)_phi              -0.50132     0.094625     -5.2979    1.2685e-07
    UtilizationRate_phi           0.39731     0.066707       5.956    2.9304e-09
    Age_phi                     -0.001167    0.0023161    -0.50386       0.61441
    Marriage_not married_phi    -0.013275     0.042627    -0.31143        0.7555

Number of observations: 2627
Log-likelihood: -3140.21

Predict EAD

EAD prediction operates on the underlying compact statistical model and then transforms the predicted values back to the EAD scale. You can specify the predict function with different options for the 'ModelLevel' name-value argument.

predictedEAD = predict(eadModel,EADData(TestInd,:),ModelLevel="ead");
predictedConversion = predict(eadModel,EADData(TestInd,:),ModelLevel="ConversionMeasure");

Validate EAD Model

For model validation, use modelDiscrimination, modelDiscriminationPlot, modelCalibration, and modelCalibrationPlot.

Use modelDiscrimination and then modelDiscriminationPlot to plot the ROC curve.

ModelLevel = "ead";

[DiscMeasure1,DiscData1] = modelDiscrimination(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel);
modelDiscriminationPlot(eadModel,EADData(TestInd, :),ModelLevel=ModelLevel,SegmentBy="Marriage");

Figure contains an axes object. The axes object with title EAD ROC Segmented by Marriage, xlabel False Positive Rate, ylabel True Positive Rate contains 2 objects of type line. These objects represent Beta, married, AUROC = 0.80597, Beta, not married, AUROC = 0.81734.

Use modelCalibration, and modelCalibrationPlot to show a scatter plot of the predictions.

YData = "Observed";

[CalMeasure1,CalData1] = modelCalibration(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel)
CalMeasure1=1×4 table
            RSquared    RMSE     Correlation    SampleMeanError
            ________    _____    ___________    _______________

    Beta    0.38655     43817      0.62173          -7393.4    


CalData1=1751×3 table
     Observed     Predicted_Beta    Residuals_Beta
    __________    ______________    ______________

         44740           18039           26701    
        54.175           10560          -10506    
        987.39           15551          -14564    
        9606.4          8407.7          1198.8    
        83.809           33318          -33234    
         73538           52120           21418    
        96.949          6598.1         -6501.2    
        873.21          5471.1         -4597.9    
        328.35            7335         -7006.6    
         55237           32580           22658    
         30359           21563          8796.4    
         39211           33177          6033.6    
    2.0885e+05      1.2586e+05           82987    
        1921.7           23319          -21397    
         15230          6565.9            8664    
         20063           11075          8987.5    
      ⋮


modelCalibrationPlot(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel,YData=YData);

Figure contains an axes object. The axes object with title Scatter Beta, R-Squared: 0.38655, xlabel EAD Predicted, ylabel EAD Observed contains 2 objects of type scatter, line. These objects represent Data, Fit.

Input Arguments

collapse all

Loss given default model, specified as a previously created Regression, Tobit, or Beta object using fitEADModel.

Data Types: object

Data, specified as a NumRows-by-NumCols table with predictor and response values. The variable names and data types must be consistent with the underlying model.

Data Types: table

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: [CalMeasure,CalData] = modelCalibration(eadModel,data(TestInd,:),DataID='Testing',CorrelationType='spearman')

Correlation type, specified as CorrelationType and a character vector or string.

Data Types: char | string

Data set identifier, specified as DataID and a character vector or string. The DataID is included in the output for reporting purposes.

Data Types: char | string

Model level, specified as ModelLevel and a character vector or string.

Note

Regression models support all three model levels, but a Tobit or Beta model supports model levels only for "ead" and "conversionMeasure".

Data Types: char | string

EAD values predicted for data by the reference model, specified as ReferenceEAD and a NumRows-by-1 numeric vector. The modelCalibration output information is reported for both the eadModel object and the reference model.

Data Types: double

Identifier for the reference model, specified as ReferenceID and a character vector or string. ReferenceID is used in the modelCalibration output for reporting purposes.

Data Types: char | string

Output Arguments

collapse all

Calibration measure, returned as a table with columns 'RSquared', 'RMSE', 'Correlation', and 'SampleMeanError'. CalMeasure has one row if only the eadModel accuracy is measured and it has two rows if reference model information is given. The row names of CalMeasure report the model ID and data ID (if provided).

Calibration data, returned as a table with observed EAD values, predicted EAD values, and residuals (observed minus predicted). Additional columns for predicted and residual values are included for the reference model, if provided. The ModelID and ReferenceID labels are appended in the column names.

More About

collapse all

Model Calibration

Model calibration measures the accuracy of the predicted probability of EAD values using different metrics.

  • R-squared — To compute the R-squared metric, modelCalibration fits a linear regression of the observed EAD values against the predicted EAD values:

    EADobs=a+b∗EADpred+ε

    The R-square of this regression is reported. For more information, see Coefficient of Determination (R-Squared).

  • RMSE — To compute the root mean square error (RMSE), modelCalibration uses the following formula where N is the number of observations:

    RMSE=1N∑i=1N(EADiobs−EADipred)2

  • Correlation — This metric is the correlation between the observed and predicted EAD:

    corr(EADobs,EADpred)

    For more information and details about the different correlation types, see corr.

  • Sample mean error — This metric is the difference between the mean observed EAD and the mean predicted EAD or, equivalently, the mean of the residuals:

    SampleMeanError=1N∑i=1N(EADiobs−EADipred)

References

[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.

[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.

[3] Brown, Iain. Developing Credit Risk Models Using SAS Enterprise Miner and SAS/STAT: Theory and Applications. SAS Institute, 2014.

[4] Roesch, Daniel and Harald Scheule. Deep Credit Risk. Independently published, 2020.

Version History

Introduced in R2023a

See Also

| | | | | | |

Topics