Main Content

modelDiscriminationPlot

Plot ROC curve

Since R2021b

collapse all in page

Syntax

modelDiscriminationPlot(eadModel,data)
modelDiscriminationPlot(___,Name=Value)
h = modelDiscriminationPlot(ax,___,Name=Value)

Description

modelDiscriminationPlot(eadModel,data) generates the receiver operating characteristic (ROC) curve. modelDiscriminationPlot supports segmentation and comparison against a reference model.

example

modelDiscriminationPlot(___,Name=Value) specifies options using one or more name-value arguments in addition to the input arguments in the previous syntax.

example

h = modelDiscriminationPlot(ax,___,Name=Value) specifies options using one or more name-value arguments in addition to the input arguments in the previous syntax and returns the figure handle h.

example

Examples

collapse all

Open Live Script

This example shows how to use fitEADModel to create a Tobit model and then use modelDiscriminationPlot to plot the ROC.

Load EAD Data

Load the EAD data. 

load EADData.mat
head(EADData)
    UtilizationRate    Age     Marriage        Limit         Drawn          EAD    
    _______________    ___    ___________    __________    __________    __________

        0.24359        25     not married         44776         10907         44740
        0.96946        44     not married    2.1405e+05    2.0751e+05         40678
              0        40     married        1.6581e+05             0    1.6567e+05
        0.53242        38     not married    1.7375e+05         92506        1593.5
         0.2583        30     not married         26258        6782.5        54.175
        0.17039        54     married        1.7357e+05         29575        576.69
        0.18586        27     not married         19590          3641        998.49
        0.85372        42     not married    2.0712e+05    1.7682e+05    1.6454e+05

rng('default');
NumObs = height(EADData);
c = cvpartition(NumObs,'HoldOut',0.4);
TrainingInd = training(c);
TestInd = test(c);

Select Model Type

Select a model type for Tobit or Regression.

ModelType = "Tobit";

Select Conversion Measure

Select a conversion measure for the EAD response values.

ConversionMeasure = "LCF";

Create Tobit EAD Model

Use fitEADModel to create a Tobit model using the TrainingInd data.

eadModel = fitEADModel(EADData(TrainingInd,:),ModelType,PredictorVars={'UtilizationRate','Age','Marriage'}, ...
    ConversionMeasure=ConversionMeasure,DrawnVar="Drawn",LimitVar="Limit",ResponseVar="EAD");
disp(eadModel);
  Tobit with properties:

        CensoringSide: "both"
            LeftLimit: 0
           RightLimit: 1
              ModelID: "Tobit"
          Description: ""
      UnderlyingModel: [1x1 risk.internal.credit.TobitModel]
        PredictorVars: ["UtilizationRate"    "Age"    "Marriage"]
          ResponseVar: "EAD"
             LimitVar: "Limit"
             DrawnVar: "Drawn"
    ConversionMeasure: "lcf"

Display the underlying model. The underlying model's response variable is the transformation of the EAD response data. Use the 'LimitVar' and 'DrawnVar' name-value arguments to modify the transformation.

disp(eadModel.UnderlyingModel);
Tobit regression model:
     EAD_lcf = max(0,min(Y*,1))
     Y* ~ 1 + UtilizationRate + Age + Marriage

Estimated coefficients:
                             Estimate         SE         tStat        pValue  
                            __________    __________    ________    __________

    (Intercept)                0.22467      0.031085      7.2276    6.4149e-13
    UtilizationRate             0.4714      0.020682      22.793             0
    Age                     -0.0014209    0.00075844     -1.8735      0.061111
    Marriage_not married     -0.010543      0.015817    -0.66654       0.50512
    (Sigma)                     0.3618     0.0049991      72.374             0

Number of observations: 2627
Number of left-censored observations: 0
Number of uncensored observations: 2626
Number of right-censored observations: 1
Log-likelihood: -1057.9

Predict EAD

EAD prediction operates on the underlying compact statistical model and then transforms the predicted values back to the EAD scale. You can specify the predict function with different options for the 'ModelLevel' name-value argument.

predictedEAD = predict(eadModel,EADData(TestInd,:),ModelLevel="ead");
predictedConversion = predict(eadModel,EADData(TestInd,:),ModelLevel="ConversionMeasure");

Validate EAD Model

For model validation, use modelDiscrimination, modelDiscriminationPlot, modelCalibration, and modelCalibrationPlot.

Use modelDiscrimination and then modelDiscriminationPlot to plot the ROC curve.

ModelLevel = "ead";

[DiscMeasure1,DiscData1] = modelDiscrimination(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel);
modelDiscriminationPlot(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel,SegmentBy="Marriage");

Figure contains an axes object. The axes object with title EAD ROC Segmented by Marriage, xlabel False Positive Rate, ylabel True Positive Rate contains 2 objects of type line. These objects represent Tobit, married, AUROC = 0.80852, Tobit, not married, AUROC = 0.81958.

Open Live Script

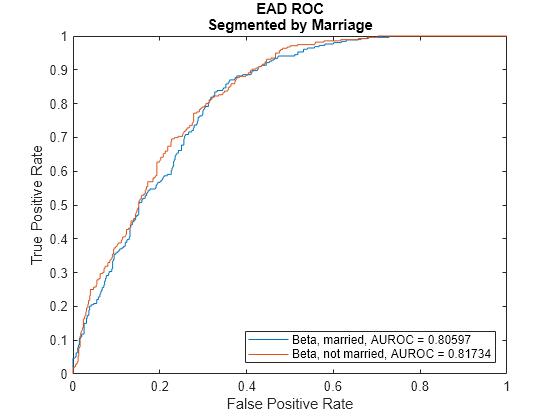
This example shows how to use fitEADModel to create a Beta model and then use modelDiscriminationPlot to plot the ROC.

Load EAD Data

Load the EAD data. 

load EADData.mat
head(EADData)
    UtilizationRate    Age     Marriage        Limit         Drawn          EAD    
    _______________    ___    ___________    __________    __________    __________

        0.24359        25     not married         44776         10907         44740
        0.96946        44     not married    2.1405e+05    2.0751e+05         40678
              0        40     married        1.6581e+05             0    1.6567e+05
        0.53242        38     not married    1.7375e+05         92506        1593.5
         0.2583        30     not married         26258        6782.5        54.175
        0.17039        54     married        1.7357e+05         29575        576.69
        0.18586        27     not married         19590          3641        998.49
        0.85372        42     not married    2.0712e+05    1.7682e+05    1.6454e+05

rng('default');
NumObs = height(EADData);
c = cvpartition(NumObs,'HoldOut',0.4);
TrainingInd = training(c);
TestInd = test(c);

Select Model Type

Select a model type for Beta.

ModelType = "Beta";

Select Conversion Measure

Select a conversion measure for the EAD response values.

ConversionMeasure = "LCF";

Create Beta EAD Model

Use fitEADModel to create a Beta model using the TrainingInd data.

eadModel = fitEADModel(EADData(TrainingInd,:),ModelType,PredictorVars={'UtilizationRate','Age','Marriage'}, ...
    ConversionMeasure=ConversionMeasure,DrawnVar="Drawn",LimitVar="Limit",ResponseVar="EAD");
disp(eadModel);
  Beta with properties:

    BoundaryTolerance: 1.0000e-07
              ModelID: "Beta"
          Description: ""
      UnderlyingModel: [1x1 risk.internal.credit.BetaModel]
        PredictorVars: ["UtilizationRate"    "Age"    "Marriage"]
          ResponseVar: "EAD"
             LimitVar: "Limit"
             DrawnVar: "Drawn"
    ConversionMeasure: "lcf"

Display the underlying model. The underlying model's response variable is the transformation of the EAD response data. Use the 'LimitVar' and 'DrawnVar' name-value arguments to modify the transformation.

disp(eadModel.UnderlyingModel);
Beta regression model:
     logit(EAD_lcf) ~ 1_mu + UtilizationRate_mu + Age_mu + Marriage_mu
     log(EAD_lcf) ~ 1_phi + UtilizationRate_phi + Age_phi + Marriage_phi

Estimated coefficients:
                                Estimate        SE         tStat        pValue  
                                _________    _________    ________    __________

    (Intercept)_mu               -0.65566      0.11484     -5.7093    1.2614e-08
    UtilizationRate_mu             1.7014     0.078094      21.787             0
    Age_mu                       -0.00559    0.0027603     -2.0252      0.042952
    Marriage_not married_mu     -0.012576     0.052098     -0.2414       0.80926
    (Intercept)_phi              -0.50132     0.094625     -5.2979    1.2685e-07
    UtilizationRate_phi           0.39731     0.066707       5.956    2.9304e-09
    Age_phi                     -0.001167    0.0023161    -0.50386       0.61441
    Marriage_not married_phi    -0.013275     0.042627    -0.31143        0.7555

Number of observations: 2627
Log-likelihood: -3140.21

Predict EAD

EAD prediction operates on the underlying compact statistical model and then transforms the predicted values back to the EAD scale. You can specify the predict function with different options for the 'ModelLevel' name-value argument.

predictedEAD = predict(eadModel,EADData(TestInd,:),ModelLevel="ead");
predictedConversion = predict(eadModel,EADData(TestInd,:),ModelLevel="ConversionMeasure");

Validate EAD Model

For model validation, use modelDiscrimination, modelDiscriminationPlot, modelCalibration, and modelCalibrationPlot.

Use modelDiscrimination and then modelDiscriminationPlot to plot the ROC curve.

ModelLevel = "ead";

[DiscMeasure1,DiscData1] = modelDiscrimination(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel);
modelDiscriminationPlot(eadModel,EADData(TestInd,:),ModelLevel=ModelLevel,SegmentBy="Marriage");

Figure contains an axes object. The axes object with title EAD ROC Segmented by Marriage, xlabel False Positive Rate, ylabel True Positive Rate contains 2 objects of type line. These objects represent Beta, married, AUROC = 0.80597, Beta, not married, AUROC = 0.81734.

Input Arguments

collapse all

Exposure at default model, specified as a previously created Regression, Tobit, or Beta object using fitEADModel.

Data Types: object

Data, specified as a NumRows-by-NumCols table with predictor and response values. The variable names and data types must be consistent with the underlying model.

Data Types: table

(Optional) Valid axis object, specified as an ax object that is created using axes. The plot will be created in the axes specified by the optional ax argument instead of in the current axes (gca). The optional argument ax must precede any of the input argument combinations.

Data Types: object

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: modelDiscriminationPlot(eadModel,data(TestInd,:),DataID='Testing',DiscretizeBy='median')

Data set identifier, specified as DataID and a character vector or string. The DataID is included in the output for reporting purposes.

Data Types: char | string

Discretization method for EAD data at the defined ModelLevel, specified as DiscretizeBy and a character vector or string.

  • 'mean' — Discretized response is 1 if observed EAD is greater than or equal to the mean EAD, 0 otherwise.

  • 'median' — Discretized response is 1 if observed EAD is greater than or equal to the median EAD, 0 otherwise.

Data Types: char | string

Name of a column in the data input, not necessarily a model variable, to be used to segment the data set, specified as SegmentBy and a character vector or string. One AUROC is reported for each segment, and the corresponding ROC data for each segment is returned in the optional output.

Data Types: char | string

Model level, specified as ModelLevel and a character vector or string.

Note

Regression models support all three model levels, but a Tobit or Beta model supports model levels only for "ead" and "conversionMeasure".

Data Types: char | string

EAD values predicted for data by the reference model, specified as ReferenceEAD and a NumRows-by-1 numeric vector. The ROC curve is plotted for both the eadModel object and the reference model.

Data Types: double

Identifier for the reference model, specified as ReferenceID and a character vector or string. 'ReferenceID' is used in the plot for reporting purposes.

Data Types: char | string

Output Arguments

collapse all

Figure handle for the line objects, returned as handle object.

More About

collapse all

Model Discrimination Plot

The modelDiscriminationPlot function plots the receiver operator characteristic (ROC) curve.

The modelDiscriminationPlot function also shows the area under the receiver operator characteristic (AUROC) curve, sometimes called simply the area under the curve (AUC). This metric is between 0 and 1 and higher values indicate better discrimination.

A numeric prediction and a binary response are needed to plot the ROC and compute the AUROC. For EAD models, the predicted EAD is used directly as the prediction. However, the observed EAD must be discretized into a binary variable. By default, observed EAD values greater than or equal to the mean observed EAD are assigned a value of 1, and values below the mean are assigned a value of 0. This discretized response is interpreted as "high EAD" vs. "low EAD." The ROC curve and the AUROC curve measure how well the predicted EAD separates the "high EAD" vs. the "low EAD" observations. You can change the level to compute the model discrimination with the ModelLevel name-value pair argument and the discretization criterion with the DiscretizeBy name-value pair argument.

The ROC curve is a parametric curve that plots the proportion of

  • High EAD cases with predicted EAD greater than or equal to a parameter t, or true positive rate (TPR)

  • Low EAD cases with predicted EAD greater than or equal to the same parameter t, or false positive rate (FPR)

The parameter t sweeps through all the observed predicted EAD values for the given data. If the AUROC value or the ROC curve data are needed programmatically, use the modelDiscrimination function. For more information about ROC curves, see ROC Curve and Performance Metrics.

References

[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.

[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.

[3] Brown, Iain. Developing Credit Risk Models Using SAS Enterprise Miner and SAS/STAT: Theory and Applications. SAS Institute, 2014.

[4] Roesch, Daniel and Harald Scheule. Deep Credit Risk. Independently published, 2020.

Version History

Introduced in R2021b

expand all

See Also

| | | | | |

Topics