besself

贝塞尔模拟滤波器设计

语法

[b,a] = besself(n,Wo)

[z,p,k] = besself(___)

[A,B,C,D] = besself(___)

说明

[b,a] = besself(n,Wo) 返回 n 阶低通模拟贝塞尔滤波器的传递函数系数，其中 Wo 是滤波器的群延迟达到大致恒定的最大角频率。n 值越大，越能产生在 Wo 范围内更好地逼近恒定的群延迟。besself 函数不支持数字贝塞尔滤波器的设计。

示例

[z,p,k] = besself(___) 设计低通模拟贝塞尔滤波器并返回其零点、极点和增益。

示例

[A,B,C,D] = besself(___) 设计模拟贝塞尔滤波器并返回指定其状态空间表示的矩阵。

示例

全部折叠

低通贝塞尔滤波器的频率响应

打开实时脚本

设计一个五阶模拟低通贝塞尔滤波器，其群延迟在频率达到 $1 0^{4}$ 弧度/秒前大致恒定。使用 freqs 绘制滤波器的幅值和相位响应。

wc = 10000;
[b,a] = besself(5,wc);
freqs(b,a)

Figure contains 2 axes objects. Axes object 1 with xlabel Frequency (rad/s), ylabel Phase (degrees) contains an object of type line. Axes object 2 with xlabel Frequency (rad/s), ylabel Magnitude contains an object of type line.

计算展开相位响应的导数的负值以得到滤波器的群延迟响应。绘制群延迟，以验证它在不超过截止频率前大致恒定。

[h,w] = freqs(b,a);
grpdel = -diff(unwrap(angle(h)))./diff(w);

clf
loglog(w(2:end),grpdel)
xlabel("Frequency (rad/s)")
ylabel("Group delay (s)")
xline(wc)
grid on

Figure contains an axes object. The axes object with xlabel Frequency (rad/s), ylabel Group delay (s) contains 2 objects of type line, constantline.

模拟和数字低通贝塞尔滤波器

打开实时脚本

从其等效模拟滤波器设计一个具有最平坦群延迟的四阶数字 IIR 滤波器。

设计一个截止频率为 300 Hz 的模拟低通四阶贝塞尔滤波器。

[b,a] = besself(4,2*pi*300);

使用冲激不变性方法将模拟滤波器转换为数字滤波器。采样率为 1000 Hz。

Fs = 10000;
[bd,ad] = impinvar(b,a,Fs);

计算模拟和数字贝塞尔滤波器的频率响应和群延迟。指定 2048 个频率点，它们在 1 Hz 到 1 kHz 之间呈几何分布。绘制群延迟响应。两种设计产生相同的结果。

f = logspace(1,3,2048);

HfAnalog = freqs(b,a,2*pi*f);
HfDigital = freqz(bd,ad,2*pi*f/Fs);
gdAnalog = -diff(unwrap(angle(HfAnalog)))./diff(2*pi*f);
gdDigital = -diff(unwrap(angle(HfDigital)))./diff(2*pi*f);

semilogx(f(2:end),gdAnalog,"-",f(2:end),gdDigital,"--")
xlabel("Frequency (Hz)")
ylabel("Group delay (sec)")
legend(["Analog","  Digital"])
grid on

Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Group delay (sec) contains 2 objects of type line. These objects represent Analog, Digital.

模拟 IIR 低通滤波器的比较

打开实时脚本

设计截止频率为 2 GHz 的五阶模拟巴特沃斯低通滤波器。乘以 $2 π$ 以将频率转换为弧度/秒。计算滤波器在 4096 个点上的频率响应。

n = 5;
wc = 2*pi*2e9;
w = 2*pi*1e9*logspace(-2,1,4096)';

[zb,pb,kb] = butter(n,wc,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,w);
gdb = -diff(unwrap(angle(hb)))./diff(wb);

设计一个具有相同边缘频率和 3 dB 通带波纹的五阶切比雪夫 I 型滤波器。计算它的频率响应。

[z1,p1,k1] = cheby1(n,3,wc,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,w);
gd1 = -diff(unwrap(angle(h1)))./diff(w1);

设计一个具有相同边缘频率和 30 dB 阻带衰减的 5 阶切比雪夫 II 型滤波器。计算它的频率响应。

[z2,p2,k2] = cheby2(n,30,wc,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,w);
gd2 = -diff(unwrap(angle(h2)))./diff(w2);

设计一个具有相同边缘频率和 3 dB 通带波纹、30 dB 阻带衰减的五阶椭圆滤波器。计算它的频率响应。

[ze,pe,ke] = ellip(n,3,30,wc,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,w);
gde = -diff(unwrap(angle(he)))./diff(we);

设计一个具有相同边缘频率的 5 阶贝塞尔滤波器。计算它的频率响应。

[zf,pf,kf] = besself(n,wc);
[bf,af] = zp2tf(zf,pf,kf);
[hf,wf] = freqs(bf,af,w);
gdf = -diff(unwrap(angle(hf)))./diff(wf);

对衰减绘图，以分贝为单位。以千兆赫为单位表示频率。比较滤波器。

fGHz = [wb w1 w2 we wf]/(2e9*pi);
plot(fGHz,mag2db(abs([hb h1 h2 he hf])))
axis([0 5 -45 5])
grid on
xlabel("Frequency (GHz)")
ylabel("Attenuation (dB)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Attenuation (dB) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

绘制采样中的群延迟。以千兆赫表示频率，以纳秒表示群延迟。比较滤波器。

gdns = [gdb gd1 gd2 gde gdf]*1e9;
gdns(gdns<0) = NaN;
loglog(fGHz(2:end,:),gdns)
grid on
xlabel("Frequency (GHz)")
ylabel("Group delay (ns)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Group delay (ns) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

巴特沃斯和切比雪夫 II 型滤波器具有平坦的通带和宽过渡带。切比雪夫 I 型和椭圆滤波器滚降更快，但有通带波纹。切比雪夫 II 型设计函数的频率输入设置阻带的起点，而不是通带的终点。贝塞尔滤波器沿通带具有大致恒定的群延迟。

输入参数

全部折叠

`n` — 滤波器阶数
最大为 25 的整数标量

滤波器阶数，指定为小于或等于 25 的整数标量。对于带通和带阻设计，n 表示滤波器阶数的一半。

数据类型: double

`Wo` — 截止频率
正标量

截止频率，指定为正标量。截止频率是滤波器群延迟大致恒定的频率范围的上界或下界。以弧度/秒为单位表示截止频率。

数据类型: double

输出参量

全部折叠

`b`, `a` — 传递函数系数
行向量

滤波器的传递函数系数，对于低通滤波器和高通滤波器，以长度为 n + 1 的行向量形式返回；对于带通滤波器和带阻滤波器，以长度为 2n + 1 的行向量形式返回。传递函数用 b 和 a 表示，如下所示：

$H (s) = \frac{b_{1} s^{r - 1} + b_{2} s^{r - 2} + \dots + b_{r}}{a_{1} s^{r - 1} + a_{2} s^{r - 2} + \dots + a_{r}}$

数据类型: double

`z`, `p`, `k` — 零点、极点和增益
列向量、标量

滤波器的零点、极点和增益，以长度为 n（对于带通和带阻设计则为 2n）的两个列向量以及标量形式返回。传递函数用 z、p 和 k 表示，如下所示：

$H (s) = k \frac{(s - z_{1}) (s - z_{2}) \dots (s - z_{r})}{(s - p_{1}) (s - p_{2}) \dots (s - p_{r})}$

数据类型: double

`A`, `B`, `C`, `D` — 状态空间矩阵
矩阵

滤波器的状态空间表示，以矩阵形式返回。如果 m = n（对于低通和高通设计）或 m = 2n（对于带通和带阻滤波器），则 A 为 m×m，B 为 m×1，C 为 1×m，而 D 为 1×1。

状态空间矩阵通过

$\begin{array}{l} \dot{x} = A x + B u \\ y = C x + D u . \end{array}$

与状态向量 x、输入 u 和输出 y 相关

数据类型: double

算法

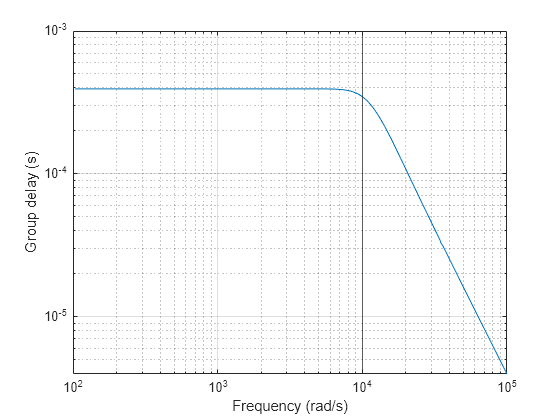
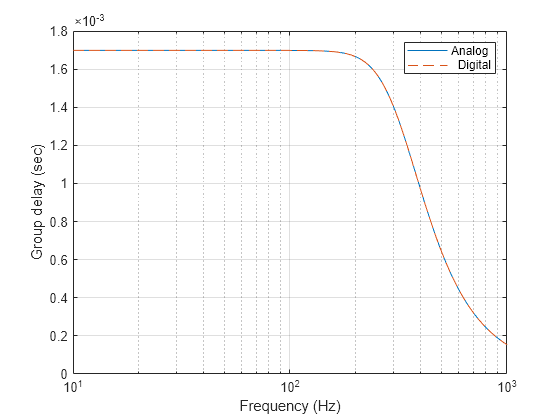
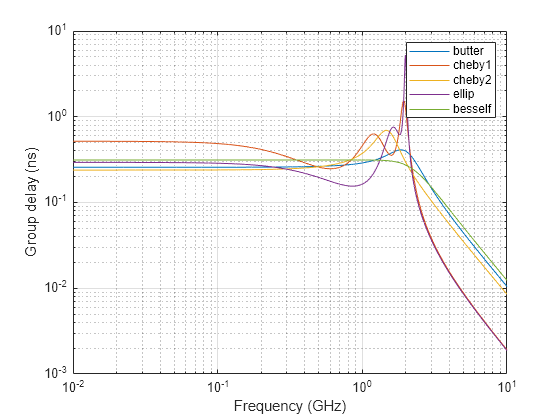
besself 设计模拟贝塞尔滤波器，其特点是在整个通带内具有几乎恒定的群延迟，从而保持通带内滤波信号的波形。

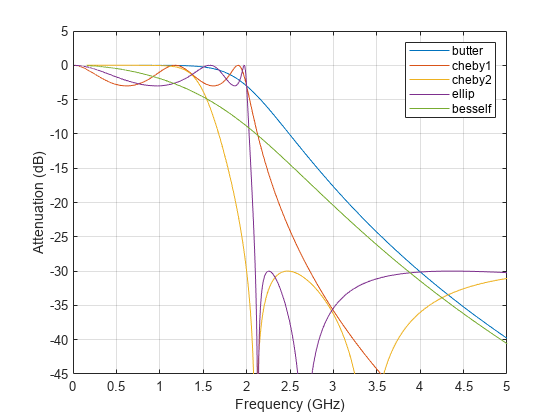
与低通巴特沃斯滤波器一样，低通贝塞尔滤波器具有单调递减的幅值响应。与巴特沃斯、切比雪夫和椭圆滤波器相比，贝塞尔滤波器具有最慢的滚降，并且需要最高阶数来满足衰减设定。

对于高阶滤波器，状态空间形式在数值上最准确，其次是零极点增益形式。传递函数系数形式最不准确；对于低至 15 阶的滤波器，可能会出现数值问题。

besself 使用一个四步算法：

使用 besselap 函数查找低通模拟原型的极点、零点和增益。
将极点、零点和增益转换为状态空间形式。
使用 lp2lp 函数将连续时间状态空间低通滤波器原型转换为具有指定截止频率的低通滤波器。
根据需要将状态空间滤波器转换回传递函数或零极点增益形式。

参考

[1] Parks, Thomas W., and C. Sidney Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987.

版本历史记录

在 R2006a 之前推出

另请参阅

besselap | butter | cheby1 | cheby2 | ellip

besself

语法

说明

示例

低通贝塞尔滤波器的频率响应

模拟和数字低通贝塞尔滤波器

模拟 IIR 低通滤波器的比较

输入参数

n — 滤波器阶数 最大为 25 的整数标量

Wo — 截止频率 正标量

输出参量

b, a — 传递函数系数 行向量

z, p, k — 零点、极点和增益 列向量、标量

A, B, C, D — 状态空间矩阵 矩阵

算法

参考

版本历史记录

另请参阅

`n` — 滤波器阶数
最大为 25 的整数标量

`Wo` — 截止频率
正标量

`b`, `a` — 传递函数系数
行向量

`z`, `p`, `k` — 零点、极点和增益
列向量、标量

`A`, `B`, `C`, `D` — 状态空间矩阵
矩阵