[B,A] = cheby1(n,Rp,Wp,"ctf") 使用二阶级联传递函数 (CTF) 设计低通数字切比雪夫 I 型滤波器。该函数返回列出滤波器传递函数的分母和分子多项式系数的矩阵，表示为级联的滤波器节。与单节传递函数相比，这种方法生成的 IIR 滤波器具有更高的数值稳定性。 (自 R2024b 起)

示例

[___] = cheby1(n,Rp,Wp,fType,"ctf") 设计低通、高通、带通或带阻数字切比雪夫 I 型滤波器，并使用 CTF 格式返回滤波器表示。得到的设计节为 2 阶（低通和高通滤波器）或 4 阶（带通和带阻滤波器）。 (自 R2024b 起)

[___,gS] = cheby1(___) 还返回系统的总增益。您必须指定 "ctf" 才能返回 gS。 (自 R2024b 起)

示例

全部折叠

低通切比雪夫 I 型传递函数

打开实时脚本

设计一个 6 阶低通切比雪夫 I 型滤波器，通带波纹为 10 dB，通带边缘频率为 300 Hz（对于以 1000 Hz 采样的数据，对应于 $0.6 π$ 弧度/采样点）。绘制其幅值和相位响应。用它对长度为 1000 个采样的随机信号进行滤波。

fc = 300;
fs = 1000;

[b,a] = cheby1(6,10,fc/(fs/2));

freqz(b,a,[],fs)

subplot(2,1,1)
ylim([-100 20])

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Frequency (Hz), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Frequency (Hz), ylabel Magnitude (dB) contains an object of type line.

dataIn = randn(1000,1);
dataOut = filter(b,a,dataIn);

带阻切比雪夫 I 型滤波器

打开实时脚本

设计一个 6 阶切比雪夫 I 型带阻滤波器，归一化边缘频率为 $0.2 π$ 和 $0.6 π$ 弧度/采样点，通带波纹为 5 dB。绘制其幅值和相位响应。用它对随机数据进行滤波。

[b,a] = cheby1(3,5,[0.2 0.6],'stop');
freqz(b,a)

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

dataIn = randn(1000,1);
dataOut = filter(b,a,dataIn);

高通切比雪夫 I 型滤波器

打开实时脚本

设计一个 9 阶高通切比雪夫 I 型滤波器，通带波纹为 0.5 dB，通带边缘频率为 300 Hz（对于以 1000 Hz 采样的数据，对应于 $0.6 π$ 弧度/采样点）。将零点、极点和增益转换为二阶节。绘制滤波器的幅值和相位响应。

[z,p,k] = cheby1(9,0.5,300/500,'high');
sos = zp2sos(z,p,k);
freqz(sos)

带通切比雪夫 I 型滤波器

打开实时脚本

设计一个 20 阶切比雪夫 I 型带通滤波器，通带频率下限为 400 Hz，通带频率上限为 560 Hz。指定通带波纹为 3 dB、采样率为 1500 Hz。使用状态空间表示。

fs = 1500;

[A,B,C,D] = cheby1(10,3,[400 560]/(fs/2));

将状态空间表示转换为二阶节，并可视化滤波器响应。

sos = ss2sos(A,B,C,D);
freqz(sos,[],fs)

使用 designfilt 设计一个相同的滤波器。可视化滤波器响应。

d = designfilt("bandpassiir",FilterOrder=20, ...
    PassbandFrequency1=400,PassbandFrequency2=560, ...
    PassbandRipple=3,SampleRate=fs);
freqz(d,[],fs)

模拟 IIR 低通滤波器的比较

打开实时脚本

设计截止频率为 2 GHz 的五阶模拟巴特沃斯低通滤波器。乘以 $2 π$ 以将频率转换为弧度/秒。计算滤波器在 4096 个点上的频率响应。

n = 5;
wc = 2*pi*2e9;
w = 2*pi*1e9*logspace(-2,1,4096)';

[zb,pb,kb] = butter(n,wc,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,w);
gdb = -diff(unwrap(angle(hb)))./diff(wb);

设计一个具有相同边缘频率和 3 dB 通带波纹的五阶切比雪夫 I 型滤波器。计算它的频率响应。

[z1,p1,k1] = cheby1(n,3,wc,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,w);
gd1 = -diff(unwrap(angle(h1)))./diff(w1);

设计一个具有相同边缘频率和 30 dB 阻带衰减的 5 阶切比雪夫 II 型滤波器。计算它的频率响应。

[z2,p2,k2] = cheby2(n,30,wc,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,w);
gd2 = -diff(unwrap(angle(h2)))./diff(w2);

设计一个具有相同边缘频率和 3 dB 通带波纹、30 dB 阻带衰减的五阶椭圆滤波器。计算它的频率响应。

[ze,pe,ke] = ellip(n,3,30,wc,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,w);
gde = -diff(unwrap(angle(he)))./diff(we);

设计一个具有相同边缘频率的 5 阶贝塞尔滤波器。计算它的频率响应。

[zf,pf,kf] = besself(n,wc);
[bf,af] = zp2tf(zf,pf,kf);
[hf,wf] = freqs(bf,af,w);
gdf = -diff(unwrap(angle(hf)))./diff(wf);

对衰减绘图，以分贝为单位。以千兆赫为单位表示频率。比较滤波器。

fGHz = [wb w1 w2 we wf]/(2e9*pi);
plot(fGHz,mag2db(abs([hb h1 h2 he hf])))
axis([0 5 -45 5])
grid on
xlabel("Frequency (GHz)")
ylabel("Attenuation (dB)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Attenuation (dB) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

绘制采样中的群延迟。以千兆赫表示频率，以纳秒表示群延迟。比较滤波器。

gdns = [gdb gd1 gd2 gde gdf]*1e9;
gdns(gdns<0) = NaN;
loglog(fGHz(2:end,:),gdns)
grid on
xlabel("Frequency (GHz)")
ylabel("Group delay (ns)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Group delay (ns) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

巴特沃斯和切比雪夫 II 型滤波器具有平坦的通带和宽过渡带。切比雪夫 I 型和椭圆滤波器滚降更快，但有通带波纹。切比雪夫 II 型设计函数的频率输入设置阻带的起点，而不是通带的终点。贝塞尔滤波器沿通带具有大致恒定的群延迟。

级联高通切比雪夫 I 型滤波器

打开实时脚本

设计一个 9 阶高通切比雪夫 I 型滤波器，截止频率为 300 Hz，采样率为 1000 Hz。通带波纹为 5 dB。以级联二阶节形式返回滤波器系统的系数。

Wn = 300/(1000/2);
[B,A] = cheby1(9,5,Wn,"high","ctf")

B = 5×3

    0.1336   -0.1336         0
    0.1336   -0.2671    0.1336
    0.1336   -0.2671    0.1336
    0.1336   -0.2671    0.1336
    0.1336   -0.2671    0.1336

A = 5×3

    1.0000    0.9022         0
    1.0000    1.6117    0.8336
    1.0000    1.1993    0.8788
    1.0000    0.8296    0.9291
    1.0000    0.6335    0.9767

绘制滤波器的幅值响应。

filterAnalyzer(B,A)

输入参数

全部折叠

`n` — 滤波器阶数
最大为 500 的整数标量

滤波器阶数，指定为小于或等于 500 的整数标量。对于带通和带阻设计，n 表示滤波器阶数的一半。

数据类型: double

`Rp` — 峰间通带波纹（以 dB 为单位）
正标量

峰间通带波纹，指定为正标量，以分贝表示。

如果您的设定 ℓ 采用线性单位，您可以使用 Rp = 40 log₁₀((1+ℓ)/(1–ℓ)) 将其转换为分贝。

数据类型: double

`Wp` — 通带边缘频率
标量 | 二元素向量

通带边缘频率，指定为标量或二元素向量。通带边缘频率是滤波器幅值响应为 -Rp 时的频率。通带波纹 Rp 的值越小，过渡带越宽。

如果 Wp 是标量，则 cheby1 设计的是边缘频率为 Wp 的低通或高通滤波器。
如果 Wp 是二元素向量 [w1 w2]，其中 w1 < w2，则 cheby1 设计的是边缘频率下限为 w1 且边缘频率上限为 w2 的带通或带阻滤波器。
对于数字滤波器，通带边缘频率必须介于 0 与 1 之间，其中 1 对应于奈奎斯特速率（即采样率的一半）或 π 弧度/采样点。
对于模拟滤波器，通带边缘频率必须用弧度/秒表示，并且可以取任何正值。

数据类型: double

`fType` — 滤波器类型
`"low"` | `"bandpass"` | `"high"` | `"stop"`

滤波器类型，指定为以下项之一：

"low" 指定通带边缘频率为 Wp 的低通滤波器。"low" 是标量 Wp 的默认值。
"high" 指定通带边缘频率为 Wp 的高通滤波器。
如果 Wp 是二元素向量，则 "bandpass" 指定阶数为 2n 的带通滤波器。当 Wp 有两个元素时，"bandpass" 是默认值。
如果 Wp 是二元素向量，则 "stop" 指定阶数为 2n 的带阻滤波器。

输出参量

全部折叠

`b,a` — 传递函数系数
行向量

滤波器的传递函数系数，以行向量形式返回。给定滤波器阶数 n，该函数返回具有 r 个采样的 b 和 a，其中：对于低通和高通滤波器，r = n+1，对于带通和带阻滤波器，r = 2*n+1。

传递函数用 b = [b₁ b₂ ⋯ b_r] 和 a = [a₁ a₂ ⋯ a_r] 表示，如下列各项之一所示：

$H (z) = \frac{b_{1} + b_{2} z^{- 1} + \dots + b_{r} z^{- (r - 1)}}{a_{1} + a_{2} z^{- 1} + \dots + a_{r} z^{- (r - 1)}}$ 用于数字滤波器。
$H (s) = \frac{b_{1} s^{r - 1} + b_{2} s^{r - 2} + \dots + b_{r}}{a_{1} s^{r - 1} + a_{2} s^{r - 2} + \dots + a_{r}}$ 用于模拟滤波器。

数据类型: double

`z,p,k` — 零点、极点和增益
列向量、标量

滤波器的零点、极点和增益，以两个列向量和一个标量形式返回。给定滤波器阶数 n，该函数返回具有 r 个采样的 z 和 p，其中：对于低通和高通滤波器，r = n，对于带通和带阻滤波器，r = 2*n。

传递函数用 z = [z₁ z₂ ⋯ z_r]、p = [p₁ p₂ ⋯ p_r] 和 k 表示，如下列各项之一所示：

$H (z) = k \frac{(1 - z_{1} z^{- 1}) (1 - z_{2} z^{- 1}) \dots (1 - z_{r} z^{- 1})}{(1 - p_{1} z^{- 1}) (1 - p_{2} z^{- 1}) \dots (1 - p_{r} z^{- 1})}$ 用于数字滤波器。
$H (s) = k \frac{(s - z_{1}) (s - z_{2}) \dots (s - z_{r})}{(s - p_{1}) (s - p_{2}) \dots (s - p_{r})}$ 用于模拟滤波器。

数据类型: double

`A,B,C,D` — 状态空间表示
矩阵

滤波器的状态空间表示，以矩阵形式返回。如果 r = n（对于低通和高通设计）或 r = 2n（对于带通和带阻滤波器），则 A 为 r×r，B 为 r×1，C 为 1×r，而 D 为 1×1。

状态空间矩阵通过以下方程组之一使状态向量 x、输入 u 和输出 y 相关。

对于数字滤波器：

$\begin{matrix} x (k + 1) = A x (k) + B u (k) \\ y (k) = C x (k) + D u (k) . \end{matrix}$
对于模拟滤波器：

$\begin{array}{l} \dot{x} = A x + B u \\ y = C x + D u . \end{array}$

数据类型: double

`B,A` — 级联传递函数 (CTF) 系数
行向量 | 矩阵

自 R2024b 起

级联传递函数 (CTF) 系数，以行向量或矩阵形式返回。B 和 A 分别列出级联传递函数的分子系数和分母系数。

B 和 A 的大小分别为 L×(m +1) 和 L×(n +1)。该函数将 A 的第一列返回为 1，因此当 A 是行向量时，A(1)=1。

L 表示滤波器节的数量。
m 表示滤波器分子的阶。
n 表示滤波器分母的阶。

cheby1 函数返回具有以下阶数设定的 CTF 系数：

m = n = 2 用于低通和高通滤波器。
m = n = 4 用于带通和带阻滤波器。

注意

要自定义 CTF 系数计算，例如在 CTF 系数中设置不同阶或自定义增益定标，请指定返回 z,p,k，然后使用 zp2ctf 获得 B,A。

有关级联传递函数格式和系数矩阵的详细信息，请参阅以 CTF 格式返回数字滤波器。

`gS` — 总系统增益
实数值标量

自 R2024b 起

总系统增益，以实数值标量形式返回。

如果指定返回 gS，则 cheby1 函数会对分子系数进行归一化，使 B 的第一列为 1，并在 gS 中返回总系统增益。
如果不指定返回 gS，则 cheby1 函数会使用 scaleFilterSections 函数将系统增益均匀分布在所有系统节上。

详细信息

全部折叠

级联传递函数

将 IIR 数字滤波器划分为级联节可提高其数值稳定性，并降低其对系数量化误差的易感性。以 L 传递函数 H₁(z)、H₂(z)、…、H_L(z) 表示的传递函数 H(z) 的级联形式为

$H (z) = \prod_{l = 1}^{L} H_{l} (z) = H_{1} (z) \times H_{2} (z) \times \dots \times H_{L} (z) .$

以 CTF 格式返回数字滤波器

指定 B 和 A 以返回滤波器系数。您也可以指定 gS 来返回滤波器的整体系统增益。通过指定这些输出参量，您可以设计用于分析、可视化和信号滤波的 CTF 格式的数字滤波器。

滤波器系数

当您指定以 CTF 格式返回分子系数和分母系数时，L 行矩阵 B 和 A 将以下列形式返回：

$B = [\begin{matrix} b_{11} & b_{12} & \dots & b_{1, m + 1} \\ b_{21} & b_{22} & \dots & b_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{L 1} & b_{L 2} & \dots & b_{L, m + 1} \end{matrix}], A = [\begin{matrix} 1 & a_{12} & \dots & a_{1, n + 1} \\ 1 & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}],$

因此滤波器的完整传递函数为

$H (z) = \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{1 + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{1 + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{1 + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}},$

其中 m ≥ 0 是滤波器的分子阶数，n ≥ 0 是分母阶数。

注意

要使用级联传递函数对信号进行滤波，请使用 ctffilt 函数。
要分析表示为级联传递函数的滤波器，请使用滤波器分析器。您还可以使用以下 Signal Processing Toolbox™ 函数来可视化和分析 CTF 格式的滤波器：
- 时域响应 - impzlength、impz 和 stepz
- 频域响应 - freqz、grpdelay、phasedelay、phasez、zerophase、zplane
- 滤波器探查 - filtord、islinphase、ismaxphase、isminphase 和 isstable

系数和增益

您可以使用输出参量三元组 [B,A,gS] 指定返回系数和整体系统增益。在这种情况下，分子系数归一化，以如下形式返回滤波器系数矩阵和增益：

$B = [\begin{matrix} 1 & β_{12} & \dots & β_{1, m + 1} \\ 1 & β_{22} & \dots & β_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & β_{L 2} & \dots & β_{L, m + 1} \end{matrix}], A = [\begin{matrix} 1 & a_{12} & \dots & a_{1, n + 1} \\ 1 & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}], g_{S},$

因此传递函数为

$H (z) = g_{S} (\frac{1 + β_{12} z^{- 1} + \dots + β_{1, m + 1} z^{- m}}{1 + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{1 + β_{22} z^{- 1} + \dots + β_{2, m + 1} z^{- m}}{1 + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{1 + β_{L 2} z^{- 1} + \dots + β_{L, m + 1} z^{- m}}{1 + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}}) .$

此传递函数等效于在滤波器系数节中定义的传递函数，其中 g_S = b₁₁×b₂₁×...×b_L1 和 β_li = b_li/b_l1 对应于 i = 1,2,…,m 和 l = 1,2,…,L。

传递函数和 CTF

传递函数语法的数值不稳定性

一般情况下，使用级联传递函数（"ctf" 语法）来设计 IIR 数字滤波器。如果使用传递函数（任何 [b,a] 语法）设计滤波器，可能会遇到数值不稳定的问题。这些不稳定性是舍入误差造成的，并且可能在阶数 n 小至 4 时出现。此示例说明了这一限制。

n = 6;
Rp = 0.6;
Fs = 200e6;
Wn = [0.5e6 6e6]/(Fs/2);
ftype = "bandpass";

% Transfer Function (TF) design
[b,a] = cheby1(n,Rp,Wn,ftype); % This is an unstable filter

% CTF design
[B,A] = cheby1(n,Rp,Wn,ftype,"ctf");

% Compare frequency responses
[hTF,f] = freqz(b,a,8192,Fs);
hCTF = freqz(B,A,8192,Fs);

semilogx(f/1e6,db(hTF),".-",f/1e6,db(hCTF))
grid on
legend(["TF Design" "CTF Design"])
xlabel("Frequency (MHz)")
ylabel("Magnitude (dB)")

Figure contains an axes object. The axes object with xlabel Frequency (MHz), ylabel Magnitude (dB) contains 2 objects of type line. These objects represent TF Design, CTF Design.

算法

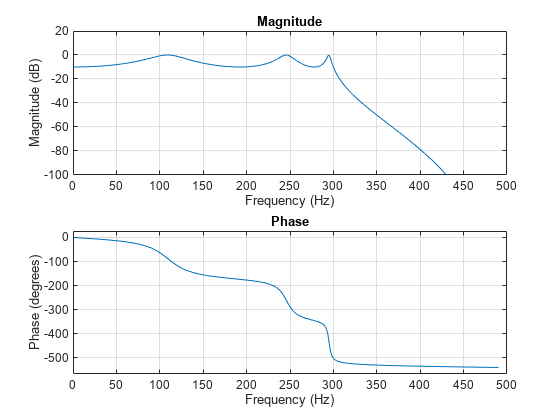
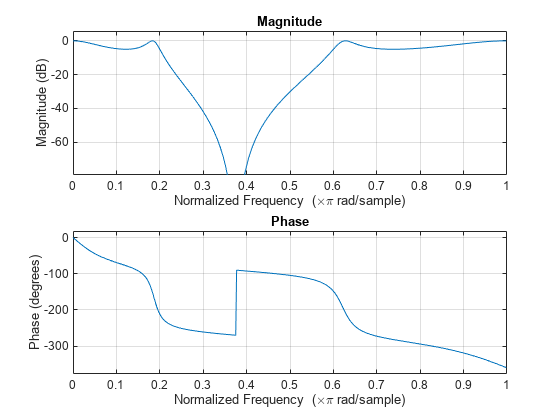
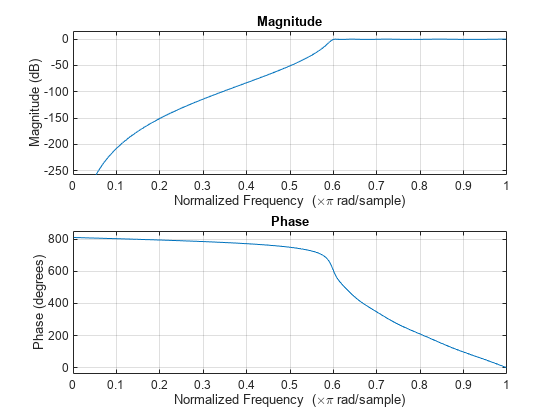
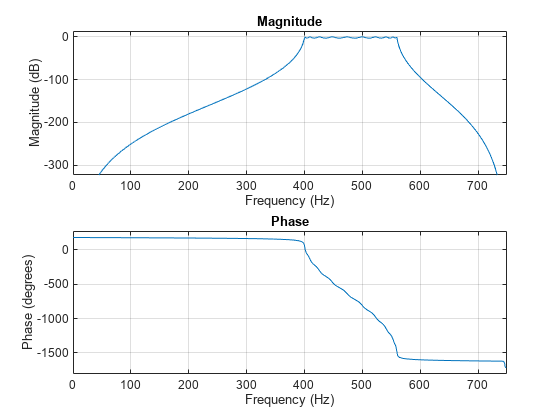
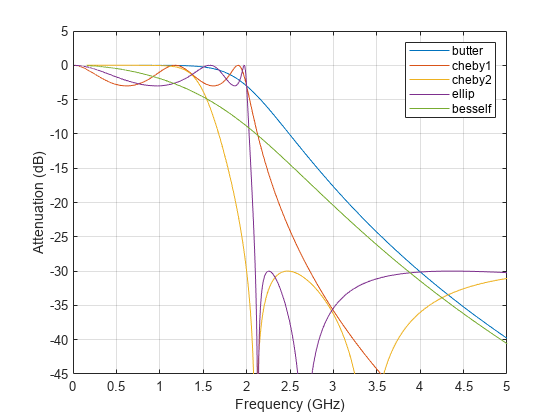
切比雪夫 I 型滤波器在通带中采用等波纹，在阻带中呈现单调性。I 型滤波器的滚降速度比 II 型滤波器快，但前者在通带内的单位偏差更大。

cheby1 使用一个五步算法：

它使用函数 cheb1ap 查找低通模拟原型的极点、零点和增益。
它将极点、零点和增益转换为状态空间形式。
如果需要，它使用状态空间变换将低通滤波器变换为具有所需频率约束的高通、带通或带阻滤波器。
对于数字滤波器设计，它使用 bilinear 通过具有频率预修正的双线性变换将模拟滤波器转换为数字滤波器。经过仔细调整频率，模拟滤波器和数字滤波器在 Wp 或 w1 和 w2 处可具有相同的频率响应幅值。
根据需要，它将状态空间滤波器转换回传递函数或零极点增益形式。

参考

[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

所有输入都必须为常量。如果表达式或变量的值不变，则可以使用这些表达式或变量。

版本历史记录

在 R2006a 之前推出

全部展开

R2024b: 使用级联传递函数设计数字滤波器

cheby1 函数支持级联传递函数 (CTF) 格式的输出。

另请参阅

App

滤波器分析器 | 滤波器设计工具

函数

besself | butter | cheb1ap | cheb1ord | cheby2 | ctffilt | designfilt | ellip | filter | freqz | sosfilt | zp2ctf

cheby1

语法

说明

示例

低通切比雪夫 I 型传递函数

带阻切比雪夫 I 型滤波器

高通切比雪夫 I 型滤波器

带通切比雪夫 I 型滤波器

模拟 IIR 低通滤波器的比较

级联高通切比雪夫 I 型滤波器

输入参数

n — 滤波器阶数 最大为 500 的整数标量

Rp — 峰间通带波纹（以 dB 为单位） 正标量

Wp — 通带边缘频率 标量 | 二元素向量

fType — 滤波器类型 "low" | "bandpass" | "high" | "stop"

输出参量

b,a — 传递函数系数 行向量

z,p,k — 零点、极点和增益 列向量、标量

A,B,C,D — 状态空间表示 矩阵

B,A — 级联传递函数 (CTF) 系数 行向量 | 矩阵

gS — 总系统增益 实数值标量

详细信息

级联传递函数

以 CTF 格式返回数字滤波器

传递函数和 CTF

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

R2024b: 使用级联传递函数设计数字滤波器

另请参阅

App

函数

`n` — 滤波器阶数
最大为 500 的整数标量

`Rp` — 峰间通带波纹（以 dB 为单位）
正标量

`Wp` — 通带边缘频率
标量 | 二元素向量

`fType` — 滤波器类型
`"low"` | `"bandpass"` | `"high"` | `"stop"`

`b,a` — 传递函数系数
行向量

`z,p,k` — 零点、极点和增益
列向量、标量

`A,B,C,D` — 状态空间表示
矩阵

`B,A` — 级联传递函数 (CTF) 系数
行向量 | 矩阵

`gS` — 总系统增益
实数值标量

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。