Main Content

cfirpm

Complex and nonlinear-phase equiripple FIR filter design

collapse all in page

Syntax

b = cfirpm(n,f,fresp)
b = cfirpm(n,f,fresp,w)
b = cfirpm(n,f,a)
b = cfirpm(n,f,a,w)
b = cfirpm(___,sym)
b = cfirpm(___,debug)
b = cfirpm(___,lgrid)
b = cfirpm(___,'skip_stage2')
[b,delta] = cfirpm(___)
[b,delta,res] = cfirpm(___)

Description

b = cfirpm(n,f,fresp) returns a length n+1 FIR filter with the best approximation to the desired response at the frequencies in f as returned by the fresp function, which is called by its function handle @fresp. For more information, see User-Defined Frequency Response Functions.

example

b = cfirpm(n,f,fresp,w) uses the weights specified by w to weight the fit in each frequency band.

b = cfirpm(n,f,a) specifies amplitudes a at the band edges in f. This syntax returns the same result as b = cfirpm(n,f,{@multiband,a}). For more information, see Predefined Frequency Response Functions.

b = cfirpm(n,f,a,w) applies an optional set of positive weights, one per band, for use during optimization. If you do not specify w, the function sets the weights to unity.

b = cfirpm(___,sym) imposes a symmetry constraint on the impulse response of the design. In addition to specifying sym, specify an input combination from any of the previous syntaxes.

example

b = cfirpm(___,debug) displays or hides the intermediate results during the filter design.

b = cfirpm(___,lgrid) controls the density of the frequency grid.

b = cfirpm(___,'skip_stage2') disables the second-stage optimization algorithm, which executes only when the cfirpm function determines that an optimal solution has not been reached by the standard firpm error-exchange. Disabling this algorithm can increase the speed of computation but incur a reduction in accuracy. By default, the second-stage optimization is enabled.

[b,delta] = cfirpm(___) returns the maximum ripple height delta.

example

[b,delta,res] = cfirpm(___) also returns the frequency response characteristics as a structure res.

Examples

collapse all

Open Live Script

Design a 30th-order linear-phase lowpass filter. Display its magnitude and phase responses.

b = cfirpm(30,[-1 -0.5 -0.4 0.7 0.8 1],@lowpass);
freqz(b,1,[],"whole")

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.

Open Live Script

Use cfirpm to design an FIR filter of order N = 22 that approximates a nonlinear-phase allpass system in the normalized frequency interval w∈[-1,1]. Compute the frequency response of the filter.

n = 22;
w = [-1 1];

b = cfirpm(n,w,"allpass");

[h,f] = freqz(b,1,[],'whole');

The cfirpm algorithm approximates a filter response given by exp(-jπwN/2+j4πw|w|). Plot the real and imaginary parts of the frequency response and overlay the target response.

gf = linspace(-1,1,256);
d = exp(-1j*pi*gf*n/2 + 4j*pi*gf.*abs(gf));

figure
subplot(2,1,1)
plot(f/pi,real(h), ...
    gf+1,fftshift(real(d)),'.')
ylabel("Real")
ylim(1.1*[-1 1])

subplot(2,1,2)
plot(f/pi,imag(h), ...
    gf+1,fftshift(imag(d)),'.')
ylabel("Imaginary")
ylim(1.1*[-1 1])

Figure contains 2 axes objects. Axes object 1 with ylabel Real contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 2 with ylabel Imaginary contains 2 objects of type line. One or more of the lines displays its values using only markers

Plot the magnitude and phase responses of the FIR filter. Express the magnitude response in dB and the phase response in degrees.

freqz(b,1,[],'whole')

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.

Open Live Script

Design a lowpass filter of order 30 using a custom frequency response function fresp. The code for the fresp function is available at the end of the example.

[b,delta]= cfirpm(30,linspace(-1,1,32),@fresp);

Visualize the magnitude response of the filter.

freqz(b,1,"whole")

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.

User-Defined fresp Function: Design a lowpass filter

The fresp function lets you choose to design a lowpass filter, a highpass filter, or a differentiator. The filter order N and frequency array F must be specified. If the frequency grid GF and weights W are unspecified, the function determines those values automatically. 

function [dh,dw] = fresp(N,F,GF,W)

W = [1;1]*(W(:).'); W = W(:);

type = 'lowpass';

mags = zeros(size(W));

switch type
    case 'lowpass'
        mags(10:end-10) = 1;
    case 'highpass'
        mags(1:10) = 1;
        mags(end-10:end) = 1;
    case 'differentiator'
        mags = abs(linspace(-pi,pi,length(mags)));
end

dh = interp1(F(:),mags,GF).*exp(-1j*pi*GF*N/2);
dw = interp1(F(:),W,GF);

end

Input Arguments

collapse all

Filter order, specified as a real positive scalar.

Normalized frequency points, specified as a real-valued vector with elements in the range [–1, 1], where 1 corresponds to the normalized Nyquist frequency. The frequencies must be in increasing order, and f must have even length. The frequency bands span f(k) to f(k+1) for k odd. The intervals f(k+1) to f(k+2) for k odd are transition bands or don't care regions during optimization.

Frequency response, specified as a function handle. For more information, see Predefined Frequency Response Functions and User-Defined Frequency Response Functions.

Desired amplitudes at the points specified in f, specified as a vector. The desired amplitude at frequencies between pairs of points f(k) and f(k+1) for k odd is the line segment connecting the points (f(k),a(k)) and (f(k+1),a(k+1)).

Weights used to adjust the fit in each frequency band, specified as a real-valued vector. The length of w is half the length of f, so exactly one weight exists per band. If you do not specify w, the function sets the weights to unity.

Symmetry constraint imposed on the impulse response of the filter design, specified as one of these values:

  • 'none' — Impose no symmetry constraint. This option is the default if you pass any negative band frequencies to the function or if fresp does not supply a default value.

  • 'even' — Impose a real and even impulse response. This option is the default for highpass, lowpass, allpass, bandpass, bandstop, inverse-sinc, and multiband designs.

  • 'odd' — Impose a real and odd impulse response. This option is the default for Hilbert and differentiator designs.

  • 'real' — Impose conjugate symmetry for the frequency response.

If you specify a value other than 'none', you must specify the band edges over only positive frequencies (the negative frequency region is filled in from symmetry). If you do not specify sym, the function queries fresp for a default setting. Any user-supplied fresp function must return a valid sym option when it is passed 'defaults' as the filter order n.

Display of intermediate results during the filter design, specified as 'off', 'trace', 'plots', or 'both'.

Density of frequency grid, specified as a cell array of an integer. The frequency grid has roughly 2^nextpow2(lgrid*n) frequency points.

Output Arguments

collapse all

Filter coefficients, returned as a row vector of length n+1.

Maximum ripple height, returned as a scalar.

Frequency response characteristics, returned as a structure. The structure res has the following fields:

Field

Description

res.fgrid

Frequency grid vector used for the filter design optimization

res.des

Desired frequency response for each point in res.fgrid

res.wt

Weighting for each point in res.fgrid

res.H

Actual frequency response for each point in res.fgrid

res.error

Error at each point in res.fgrid (res.des-res.H)

res.iextr

Vector of indices into res.fgrid for extremal frequencies

res.fextr

Vector of extremal frequencies

More About

collapse all

Predefined Frequency Response Functions

Predefined fresp frequency response functions are included for a number of common filter designs in this section. For more information on how to create a custom fresp function, see Create Function Handle.

For all of the predefined frequency response functions, the symmetry option sym defaults to 'even' if f contains no negative frequencies and d = 0. Otherwise sym defaults to 'none'. For details, see sym. For all of the predefined frequency response functions, d specifies a group-delay offset such that the filter response has a group delay of n/2+d in units of the sample interval. Negative values create less delay, and positive values create more delay. By default, d = 0.

  • @lowpass, @highpass, @allpass, @bandpass, @bandstop

    These functions share a common syntax, exemplified by @lowpass.

    b = cfirpm(n,f,@lowpass,...) and

    b = cfirpm(n,f,{@lowpass,d},...) design a linear-phase (n/2+d delay) filter.

    Note

    For @bandpass filters, the first element in the frequency vector must be less than or equal to zero and the last element must be greater than or equal to zero.

  • @multiband designs a linear-phase frequency response filter with arbitrary band amplitudes.

    b = cfirpm(n,f,{@multiband,a},...) and

    b = cfirpm(n,f,{@multiband,a,d},...) specify vector a containing the desired amplitudes at the band edges in f. The desired amplitude at frequencies between pairs of points f(k) and f(k+1) for k odd is the line segment connecting the points (f(k),a(k)) and (f(k+1),a(k+1)).

  • @differentiator designs a linear-phase differentiator. For these designs, zero-frequency must be in a transition band, and band weighting is set to be inversely proportional to frequency.

    b = cfirpm(n,f,{@differentiator,fs},...) and

    b = cfirpm(n,f,{@differentiator,fs,d},...) specify the sample rate fs used to determine the slope of the differentiator response. If omitted, fs defaults to 1.

  • @hilbfilt designs a linear-phase Hilbert transform filter response. For Hilbert designs, zero-frequency must be in a transition band.

    b = cfirpm(n,f,@hilbfilt,...) and

    b = cfirpm(N,F,{@hilbfilt,d},...) design a linear-phase (n/2+d delay) Hilbert transform filter.

  • @invsinc designs a linear-phase inverse-sinc filter response.

    b = cfirpm(n,f,{@invsinc,a},...) and

    b = cfirpm(n,f,{@invsinc,a,d},...) specify gain a for the sinc function, computed as sinc(a*g), where g contains the optimization grid frequencies normalized to the range [–1, 1]. By default, a = 1. The group-delay offset is d such that the filter response has a group delay of n/2+d in units of the sample interval, where n is the filter order. Negative values create less delay, and positive values create more delay. By default, d = 0.

User-Defined Frequency Response Functions

Instead of the predefined frequency response functions for fresp, you can use a user-defined function.

The cfirpm function calls this user-defined function using this syntax.

[dh,dw] = fresp(n,f,gf,w,p1,p2,...)

  • n is the filter order.

  • f is the vector of frequency band edges that appear monotonically between –1 and 1, where 1 corresponds to the Nyquist frequency.

  • gf is a vector of grid points that have been linearly interpolated over each specified frequency band by cfirpm. The input gf determines the frequency grid at which the response function must be evaluated. The cfirpm function returns this data in the fgrid field of the res structure.

  • w is a vector of real, positive weights, one per band, used during optimization. w is optional in the call to cfirpm. If you do not specify this input, cfirpm sets it to unity weighting before passing it to fresp.

  • dh and dw are the desired complex frequency response and band weight vectors, respectively, that are evaluated at each frequency in grid gf.

  • p1,p2,... are optional parameters that can be passed to fresp.

Additionally, the cfirpm function makes a preliminary call to fresp to determine the default symmetry sym. cfirpm makes this call using this syntax.

sym = fresp('defaults',{n,f,[],w,p1,p2,...})
The arguments can be used in determining an appropriate symmetry default as necessary. You can use the local function lowpass as a template for generating new frequency response functions. To find the lowpass function, enter edit cfirpm at the command line and search for lowpass in the cfirpm function code. You can copy the function, modify it, rename it, and save it in your path.

Algorithms

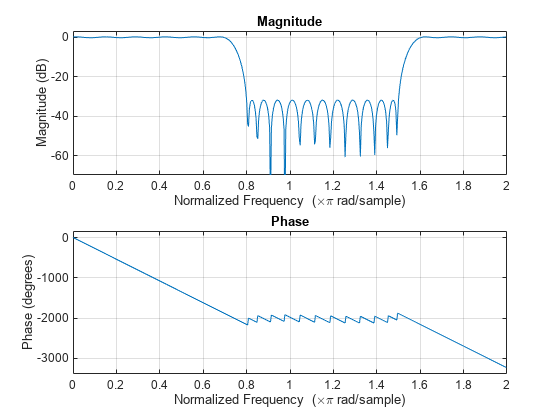
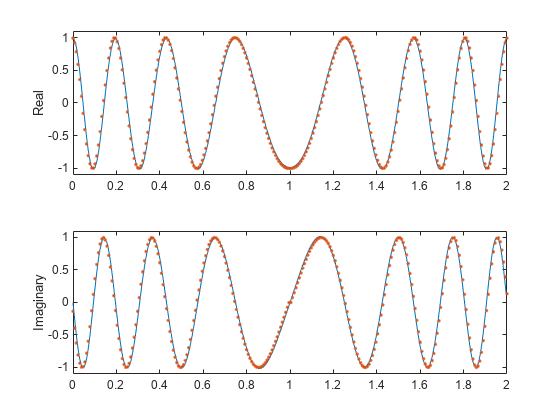
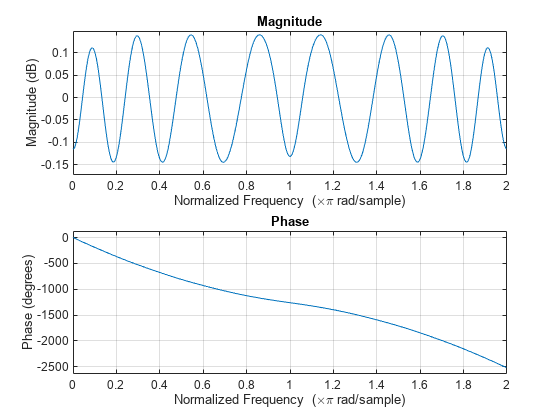
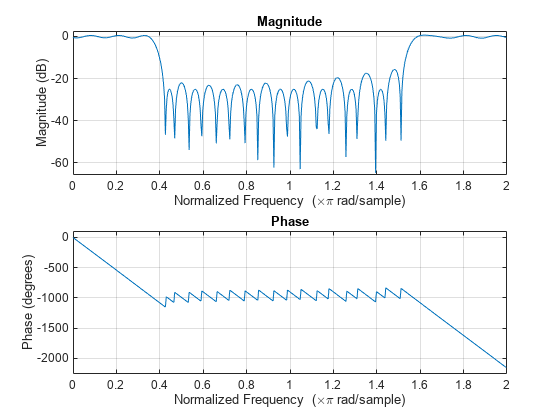
The cfirpm function enables you to specify arbitrary frequency-domain constraints for the design of a possibly complex FIR filter. The Chebyshev (or minimax) filter error is optimized, producing equiripple FIR filter designs.

An extended version of the Remez exchange method is implemented for the complex case. This exchange method obtains the optimal filter when the equiripple nature of the filter is restricted to have n+2 extrema. When the filter does not converge, the algorithm switches to an ascent-descent algorithm that takes over to finish the convergence to the optimal solution. For further details, see the references.

References

[1] Demjanjov, V. F., and V. N. Malozemov. Introduction to Minimax. New York: John Wiley & Sons, 1974.

[2] Karam, L.J. Design of Complex Digital FIR Filters in the Chebyshev Sense. Ph.D. Thesis, Georgia Institute of Technology, March 1995.

[3] Karam, L.J., and J. H. McClellan. "Complex Chebyshev Approximation for FIR Filter Design." IEEE® Transactions on Circuits and Systems II: Analog and Digital Signal Processing 42, no. 3 (March 1995): 207–216.

Extended Capabilities

Version History

Introduced before R2006a

See Also

Apps

Functions