fir2
基于频率采样的 FIR 滤波器设计
说明
示例
加载 MAT 文件 chirp。该文件包含信号 y（以频率 Fs = 8192 Hz 采样）。该信号的大部分功率高于 Fs/4 = 2048 Hz，即奈奎斯特频率的一半。向信号添加随机噪声。
load chirp
y = y + randn(size(y))/25;
t = (0:length(y)-1)/Fs;设计一个 34 阶 FIR 高通滤波器，以衰减低于 Fs/4 的信号的分量。指定归一化截止频率为 0.48，对应约 1966 Hz。可视化该滤波器的频率响应。
f = [0 0.48 0.48 1]; mhi = [0 0 1 1]; bhi = fir2(34,f,mhi); freqz(bhi,1,[],Fs)
对啁啾信号进行滤波。对滤波前后的信号绘图。
outhi = filter(bhi,1,y); figure subplot(2,1,1) plot(t,y) title('Original Signal') ylim([-1.2 1.2]) subplot(2,1,2) plot(t,outhi) title('Highpass Filtered Signal') xlabel('Time (s)') ylim([-1.2 1.2])
将滤波器从高通更改为低通。使用相同的阶数和截止频率。再次对信号进行滤波。结果大多是噪声。
mlo = [1 1 0 0]; blo = fir2(34,f,mlo); outlo = filter(blo,1,y); subplot(2,1,1) plot(t,y) title('Original Signal') ylim([-1.2 1.2]) subplot(2,1,2) plot(t,outlo) title('Lowpass Filtered Signal') xlabel('Time (s)') ylim([-1.2 1.2])
设计一个 30 阶低通滤波器，归一化截止频率为 弧度/采样点。对叠加实际频率响应的理想频率响应绘图。
f = [0 0.6 0.6 1]; m = [1 1 0 0]; b1 = fir2(30,f,m); [h1,w] = freqz(b1,1); plot(f,m,w/pi,abs(h1)) xlabel('\omega / \pi') lgs = {'Ideal','fir2 default'}; legend(lgs)
使用一个包含 64 个点的插值网格重新设计滤波器。
b2 = fir2(30,f,m,64); h2 = freqz(b2,1); hold on plot(w/pi,abs(h2)) lgs{3} = 'npt = 64'; legend(lgs)
使用包含 64 个点的插值网格和截止频率周围包含 13 个点的区间重新设计滤波器。
b3 = fir2(30,f,m,64,13);
h3 = freqz(b3,1);
plot(w/pi,abs(h3))
lgs{4} = 'lap = 13';
legend(lgs)
设计具有以下频率响应的 FIR 滤波器：
介于 0 与 弧度/采样点之间的正弦波。
F1 = 0:0.01:0.18; A1 = 0.5+sin(2*pi*7.5*F1)/4;
介于 与 弧度/采样点之间的分段线性部分。
F2 = [0.2 0.38 0.4 0.55 0.562 0.585 0.6 0.78]; A2 = [0.5 2.3 1 1 -0.2 -0.2 1 1];
介于 弧度/采样点与奈奎斯特频率之间的二次部分。
F3 = 0.79:0.01:1; A3 = 0.2+18*(1-F3).^2;
使用汉明窗设计滤波器。将滤波器阶数指定为 50。
N = 50; FreqVect = [F1 F2 F3]; AmplVect = [A1 A2 A3]; ham = fir2(N,FreqVect,AmplVect);
使用形状参数为 3 的凯塞窗重复计算。
kai = fir2(N,FreqVect,AmplVect,kaiser(N+1,3));
使用 designfilt 函数重新设计滤波器。designfilt 默认使用矩形窗。计算滤波器在 1024 个点上的零相位响应。
d = designfilt('arbmagfir','FilterOrder',N, ... 'Frequencies',FreqVect,'Amplitudes',AmplVect); [zd,wd] = zerophase(d,1024);
显示三个滤波器的零相位响应。叠加理想响应。
zerophase(ham,1) hold on zerophase(kai,1) plot(wd/pi,zd) plot(FreqVect,AmplVect,'k:') legend('Hamming','Kaiser','designfilt','ideal')
输入参数
输出参量
算法
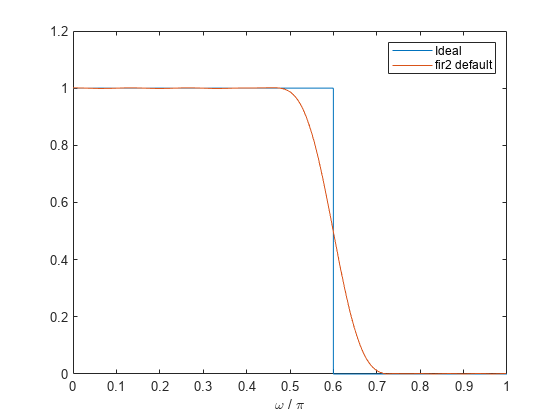
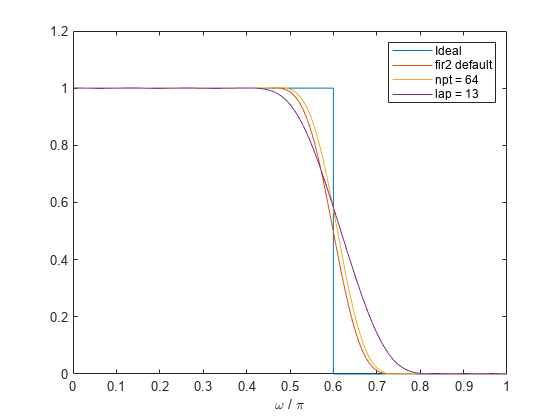
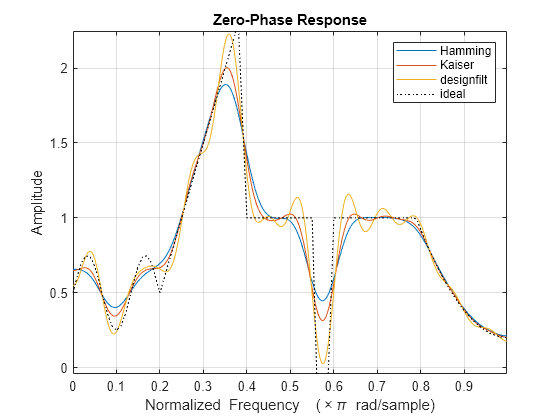
fir2 使用频率采样设计滤波器。该函数将所需的频率响应线性插值到长度为 npt 的密集、等间距网格上。fir2 还在 f 的重复值周围设置包含 lap 个点的区域以提供陡峭但平滑的过渡。为了获得滤波器系数，该函数对网格应用快速傅里叶逆变换并乘以 window。
参考
[1] Jackson, L. B. Digital Filters and Signal Processing. 3rd Ed. Boston: Kluwer Academic Publishers, 1996.
[2] Mitra, Sanjit K. Digital Signal Processing: A Computer Based Approach. New York: McGraw-Hill, 1998.
扩展功能
版本历史记录
在 R2006a 之前推出
