firpm

Parks-McClellan optimal FIR filter design

collapse all in page

Syntax

b = firpm(n,f,a)

b = firpm(n,f,a,w)

b = firpm(n,f,a,ftype)

b = firpm(n,f,a,lgrid)

[b,err] = firpm(___)

[b,err,res] = firpm(___)

b = firpm(n,f,fresp,w)

b = firpm(n,f,fresp,w,ftype)

Description

b = firpm(n,f,a) returns row vector b containing the n+1 coefficients of an order-n FIR filter. The frequency and amplitude characteristics of the resulting filter match those given by vectors f and a.

example

b = firpm(n,f,a,w) uses w to weigh the frequency bins.

example

b = firpm(n,f,a,ftype) uses a filter type specified by 'ftype'.

b = firpm(n,f,a,lgrid) uses the integer lgrid to control the density of the frequency grid.

[b,err] = firpm(___) returns the maximum ripple height in err. You can use this with any of the previous input syntaxes.

[b,err,res] = firpm(___) returns the frequency response characteristics as a structure res.

b = firpm(n,f,fresp,w) returns an FIR filter whose frequency-amplitude characteristics best approximate the response returned by function handle fresp.

b = firpm(n,f,fresp,w,ftype) designs antisymmetric (odd) filters, where ftype specifies the filter as a differentiator or Hilbert transformer. If you do not specify an ftype, a call is made to fresp to determine the default symmetry property.

Examples

collapse all

Parks-McClellan Bandpass Filter

Open Live Script

Use the Parks-McClellan algorithm to design an FIR bandpass filter of order 17. Specify normalized stopband frequencies of $0.3 π$ and $0.7 π$ rad/sample and normalized passband frequencies of $0.4 π$ and $0.6 π$ rad/sample. Plot the ideal and actual magnitude responses.

f = [0 0.3 0.4 0.6 0.7 1];
a = [0 0 1 1 0 0];
b = firpm(17,f,a);

[h,w] = freqz(b,1,512);
plot(f,a,w/pi,abs(h))
legend('Ideal','firpm Design')
xlabel 'Radian Frequency (\omega/\pi)', ylabel 'Magnitude'

Figure contains an axes object. The axes object with xlabel Radian Frequency ( omega / pi ), ylabel Magnitude contains 2 objects of type line. These objects represent Ideal, firpm Design.

Parks-McClellan Lowpass Filter

Open Live Script

Design a lowpass filter with a 1500 Hz passband cutoff frequency and 2000 Hz stopband cutoff frequency. Specify a sampling frequency of 8000 Hz. Require a maximum stopband amplitude of 0.01 and a maximum passband error (ripple) of 0.001. Obtain the required filter order, normalized frequency band edges, frequency band amplitudes, and weights using firpmord.

[n,fo,ao,w] = firpmord([1500 2000],[1 0],[0.001 0.01],8000);
b = firpm(n,fo,ao,w);
freqz(b,1,[],8000)

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Frequency (kHz), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Frequency (kHz), ylabel Magnitude (dB) contains an object of type line.

FIR Bandpass Filter with Asymmetric Attenuation

Open Live Script

Use the Parks-McClellan algorithm to create a 50th-order equiripple FIR bandpass filter to be used with signals sampled at 1 kHz.

N = 50;
Fs = 1e3;

Specify that the passband spans the frequencies between 200 Hz and 300 Hz and that the transition region on either side of the passband has a width of 50 Hz.

Fstop1 = 150;
Fpass1 = 200;
Fpass2 = 300;
Fstop2 = 350;

Design the filter so that the optimization fit weights the low-frequency stopband with a weight of 3, the passband with a weight of 1, and the high-frequency stopband with a weight of 100. Display the magnitude response of the filter.

Wstop1 = 3;
Wpass = 1;
Wstop2 = 100;

b = firpm(N,[0 Fstop1 Fpass1 Fpass2 Fstop2 Fs/2]/(Fs/2), ...
    [0 0 1 1 0 0],[Wstop1 Wpass Wstop2]);

freqz(b,1)

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

Input Arguments

collapse all

`n` — Filter order
real positive scalar

Filter order, specified as a real positive scalar.

`f` — Normalized frequency points
real-valued vector with elements in the range [0, 1]

Normalized frequency points, specified as a real-valued vector. The argument must be in the range [0, 1] , where 1 corresponds to the Nyquist frequency. The number of elements in the vector is always a multiple of 2. The frequencies must be in increasing order.

`a` — Desired amplitude
vector

Desired amplitudes at the points specified in f, specified as a vector. f and a must be the same length. The length must be an even number.

The desired amplitude at frequencies between pairs of points (f(k), f(k+1)) for k odd is the line segment connecting the points (f(k), a(k)) and (f(k+1), a(k+1)).
The desired amplitude at frequencies between pairs of points (f(k), f(k+1)) for k even is unspecified. The areas between such points are transition regions or regions that are not important for a particular application.

`w` — Weights
real-valued vector

Weights used to adjust the fit in each frequency band, specified as a real-valued vector. The length of w is half the length of f and a, so there is exactly one weight per band.

`ftype` — Filter type
`'hilbert'` | `'differentiator'`

Filter type for linear-phase filters with odd symmetry (type III and type IV), specified as either 'hilbert' or 'differentiator':

'hilbert' — The output coefficients in b obey the relation b(k) = –b(n + 2 – k), k = 1, ..., n + 1. This class of filters includes the Hilbert transformer, which has a desired amplitude of 1 across the entire band.
For example,
```
h = firpm(30,[0.1 0.9],[1 1],'hilbert');
```
designs an approximate FIR Hilbert transformer of length 31.
'differentiator' — For nonzero amplitude bands, the filter weighs the error by a factor of 1/f so that the error at low frequencies is much smaller than at high frequencies. For FIR differentiators, which have an amplitude characteristic proportional to frequency, these filters minimize the maximum relative error (the maximum of the ratio of the error to the desired amplitude).

`lgrid` — Density of frequency grid
`16` (default) | 1-by-1 cell array with integer value

Control the density of the frequency grid, which has roughly (lgrid*n)/(2*bw) frequency points, where bw is the fraction of the total frequency band interval [0,1] covered by f. Increasing lgrid often results in filters that more exactly match an equiripple filter, but that take longer to compute. The default value of 16 is the minimum value that should be specified for lgrid.

`fresp` — Frequency response
function handle

Frequency response, specified as a function handle. For more information, see Frequency Response Functions.

Output Arguments

collapse all

`b` — Filter coefficients
row vector

Filter coefficients, returned as a row vector of length n + 1. The coefficients are in increasing order.

`err` — Maximum ripple height
scalar

Maximum ripple height, returned as a scalar.

`res` — Frequency response characteristics
structure

Frequency response characteristics, returned as a structure. The structure res has the following fields:

`res.fgrid`	Frequency grid vector used for the filter design optimization
`res.des`	Desired frequency response for each point in `res.fgrid`
`res.wt`	Weighting for each point in `res.fgrid`
`res.H`	Actual frequency response for each point in `res.fgrid`
`res.error`	Error at each point in `res.fgrid` (`res.des-res.H`)
`res.iextr`	Vector of indices into `res.fgrid` for extremal frequencies
`res.fextr`	Vector of extremal frequencies

More About

collapse all

Frequency Response Functions

The predefined frequency response function handle for firpm is @firpmfrf, which designs a linear-phase FIR filter. The b = firpm(n,f,a,w) command is equivalent to b = firpm(n,f,{@firpmfrf,a},w). If desired, you can write your own response function. Use help private/firpmfrf and see Create Function Handle for more information.

User-Defined Frequency Response Functions

Instead of the firpmfrf predefined frequency response function for fresp, you can use a user-defined function.

The firpm function calls this user-defined function using this syntax.

[dh,dw] = fresp(n,f,gf,w,p1,p2,...)

n is the filter order.
f is the vector of frequency band edges that appear monotonically between 0 and 1, where 1 corresponds to the Nyquist frequency.
gf is a vector of grid points that have been linearly interpolated over each specified frequency band by firpm. The input gf determines the frequency grid at which the response function must be evaluated. The firpm function returns this data in the fgrid field of the res structure.
w is a vector of real, positive weights, one per band, used during optimization. w is optional in the call to firpm. If you do not specify this input, firpm sets it to unity weighting before passing it to fresp.
dh and dw are the desired complex frequency response and band weight vectors, respectively, that are evaluated at each frequency in grid gf.
p1,p2,... are optional parameters that can be passed to fresp.

Additionally, the firpm function makes a preliminary call to fresp to determine the default symmetry sym. firpm makes this call using this syntax.

sym = fresp('defaults',{n,f,[],w,p1,p2,...})

The arguments can be used in determining an appropriate symmetry default as necessary. You can use the firpmfrf function as a template for generating new frequency response functions. To find the firpmfrf function, enter

edit
                        private/firpmfrf

. You can copy the function, modify it, rename it, and save it in your path.

Tips

If your filter design fails to converge, the filter design might not be correct. Verify the design by checking the frequency response.

If your filter design fails to converge and the resulting filter design is not correct, attempt one or more of the following:

Increase the filter order.
Relax the filter design by reducing the attenuation in the stopbands and/or broadening the transition regions.

Algorithms

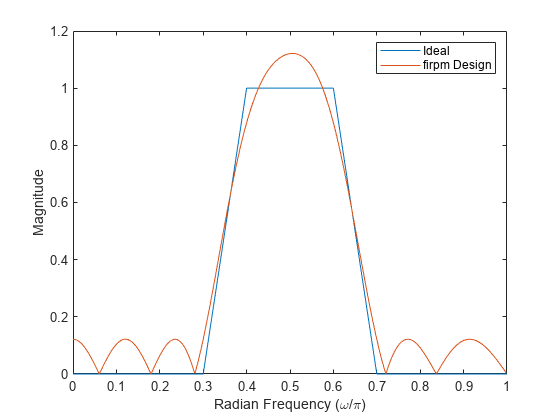
firpm designs a linear-phase FIR filter using the Parks-McClellan algorithm [2]. The Parks-McClellan algorithm uses the Remez exchange algorithm and Chebyshev approximation theory to design filters with an optimal fit between the desired and actual frequency responses. The filters are optimal in the sense that the maximum error between the desired frequency response and the actual frequency response is minimized. Filters designed this way exhibit an equiripple behavior in their frequency responses and are sometimes called equiripple filters. firpm exhibits discontinuities at the head and tail of its impulse response due to this equiripple nature.

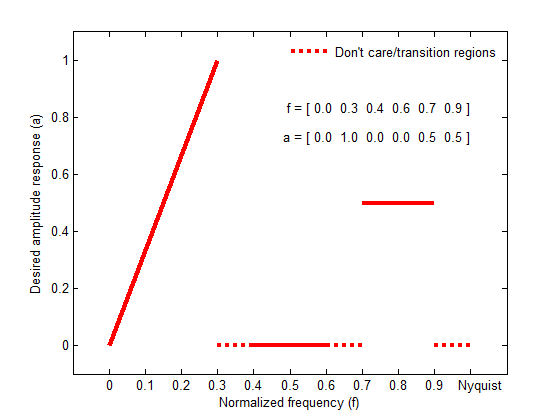
These are type I (n odd) and type II (n even) linear-phase filters. Vectors f and a specify the frequency-amplitude characteristics of the filter:

f is a vector of pairs of frequency points, specified in the range between 0 and 1, where 1 corresponds to the Nyquist frequency. The frequencies must be in increasing order.
a is a vector containing the desired amplitude at the points specified in f.
The desired amplitude function at frequencies between pairs of points (f(k), f(k+1)) for k odd is the line segment connecting the points (f(k), a(k)) and (f(k+1), a(k+1)).
The desired amplitude function at frequencies between pairs of points (f(k), f(k+1)) for k even is unspecified. These are transition or "don’t care" regions.
f and a are the same length. This length must be an even number.

The figure below illustrates the relationship between the f and a vectors in defining a desired amplitude response.

Desired amplitude response vs. normalized frequency. The plot includes the don't-care and transition regions.

firpm always uses an even filter order for configurations with even symmetry and a nonzero passband at the Nyquist frequency. The reason for the even filter order is that for impulse responses exhibiting even symmetry and odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, firpm increments it by 1.

firpm designs type I, II, III, and IV linear-phase filters. Type I and type II are the defaults for n even and n odd, respectively, while type III (n even) and type IV (n odd) are specified with 'hilbert' or 'differentiator', respectively, using the ftype argument. The different types of filters have different symmetries and certain constraints on their frequency responses. (See [3] for more details.)

Linear Phase Filter Type	Filter Order	Symmetry of Coefficients	Response H(f), f `=` 0	Response H(f), f `=` 1 (Nyquist)
Type I	Even	even: $b (k) = b (n + 2 - k), k = 1, ..., n + 1$	No restriction	No restriction
Type II	Odd	even: $b (k) = b (n + 2 - k), k = 1, ..., n + 1$	No restriction	H(1) `=` 0 `firpm` increments the filter order by 1 if you attempt to construct a type II filter with a nonzero passband at the Nyquist frequency.
Type III	Even	odd: $b (k) = - b (n + 2 - k), k = 1, ..., n + 1$	H(0) `=` 0	H(1) `=` 0
Type IV	Odd	odd: $b (k) = - b (n + 2 - k), k = 1, ..., n + 1$	H(0) `=` 0	No restriction

You can also use firpm to write a function that defines the desired frequency response. For more information, see User-Defined Frequency Response Functions.

References

[1] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Selected Papers in Digital Signal Processing. Vol. II. New York: IEEE Press, 1976.

[2] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979, algorithm 5.1.

[3] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, p. 486.

[4] Parks, Thomas W., and C. Sidney Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987, p. 83.

[5] Rabiner, Lawrence R., James H. McClellan, and Thomas W. Parks. "FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximation." Proceedings of the IEEE^®. Vol. 63, Number 4, 1975, pp. 595–610.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

All inputs must be constants. Expressions or variables are allowed if their values do not change.

Version History

Introduced before R2006a

firpm

Syntax

Description

Examples

Parks-McClellan Bandpass Filter

Parks-McClellan Lowpass Filter

FIR Bandpass Filter with Asymmetric Attenuation

Input Arguments

`n` — Filter order
real positive scalar

`f` — Normalized frequency points
real-valued vector with elements in the range [0, 1]

`a` — Desired amplitude
vector

`w` — Weights
real-valued vector

`ftype` — Filter type
`'hilbert'` | `'differentiator'`

`lgrid` — Density of frequency grid
`16` (default) | 1-by-1 cell array with integer value

`fresp` — Frequency response
function handle

Output Arguments

`b` — Filter coefficients
row vector

`err` — Maximum ripple height
scalar

`res` — Frequency response characteristics
structure

More About

Frequency Response Functions

Tips

Algorithms

References

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

See Also

Apps

Functions

firpm

Syntax

Description

Examples

Parks-McClellan Bandpass Filter

Parks-McClellan Lowpass Filter

FIR Bandpass Filter with Asymmetric Attenuation

Input Arguments

n — Filter order real positive scalar

f — Normalized frequency points real-valued vector with elements in the range [0, 1]

a — Desired amplitude vector

w — Weights real-valued vector

ftype — Filter type 'hilbert' | 'differentiator'

lgrid — Density of frequency grid 16 (default) | 1-by-1 cell array with integer value

fresp — Frequency response function handle

Output Arguments

b — Filter coefficients row vector

err — Maximum ripple height scalar

res — Frequency response characteristics structure

More About

Frequency Response Functions

Tips

Algorithms

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Version History

See Also

Apps

Functions

`n` — Filter order
real positive scalar

`f` — Normalized frequency points
real-valued vector with elements in the range [0, 1]

`a` — Desired amplitude
vector

`w` — Weights
real-valued vector

`ftype` — Filter type
`'hilbert'` | `'differentiator'`

`lgrid` — Density of frequency grid
`16` (default) | 1-by-1 cell array with integer value

`fresp` — Frequency response
function handle

`b` — Filter coefficients
row vector

`err` — Maximum ripple height
scalar

`res` — Frequency response characteristics
structure

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.