rainflow

疲劳分析的雨流计数

全页折叠

语法

c = rainflow(x)
c = rainflow(x,fs)
c = rainflow(x,t)
c = rainflow(xt)
c = rainflow(___,'ext')
[c,rm,rmr,rmm] = rainflow(___)
[c,rm,rmr,rmm,idx] = rainflow(___)
rainflow(___)

说明

c = rainflow(x) 根据 ASTM E 1049 标准返回加载时间历史记录 x 的周期计数。有关详细信息，请参阅算法。

c = rainflow(x,fs) 返回以 fs 速率采样的 x 的周期计数。

示例

c = rainflow(x,t) 返回以存储在 t 中的时间值采样的 x 的周期计数。

示例

c = rainflow(xt) 返回存储在 MATLAB® 时间表 xt 中的时间历史记录的周期计数。

示例

c = rainflow(___,'ext') 将时间历史记录指定为已标识的反转（波峰和波谷）的向量。'ext' 可以与上述任一语法结合使用。

示例

[c,rm,rmr,rmm] = rainflow(___) 输出一个雨流矩阵 rm 以及两个向量 rmr 和 rmm，分别包含 rm 的行和列的直方图 bin 边界。

[c,rm,rmr,rmm,idx] = rainflow(___) 还返回在输入中标识的反转的线性索引。

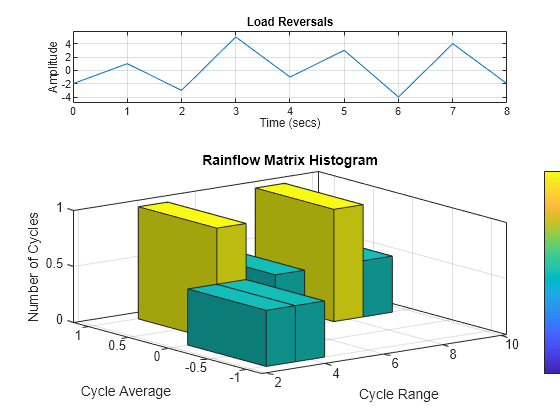
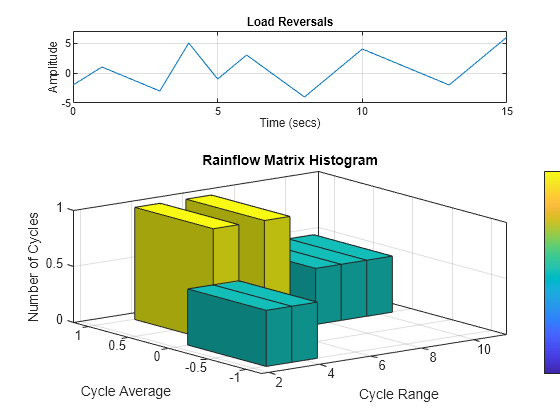
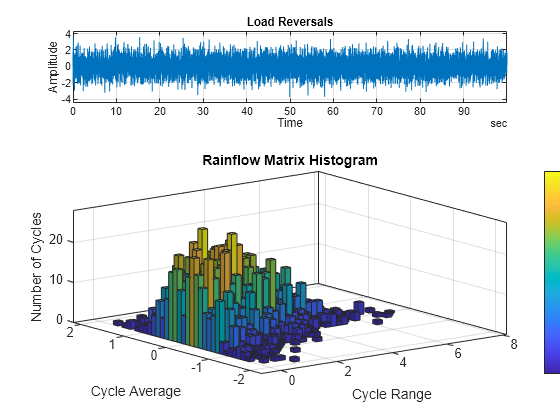
不带输出参量的 rainflow(___) 在当前图窗中绘制加载反转和雨流矩阵直方图。

示例

全部折叠

打开实时脚本

生成类似于加载历史记录的信号，该信号由连接已知的等间距反转的正弦半周期组成。该信号在 512 Hz 下采样 8 秒。绘制极值和信号。

fs = 512;

X = [-2 1 -3 5 -1 3 -4 4 -2];
lX = length(X)-1;

Y = -diff(X)/2.*cos(pi*(0:1/fs:1-1/fs)') + (X(1:lX)+X(2:lX+1))/2;
Y = [Y(:);X(end)];

plot(0:lX,X,"o",0:1/fs:lX,Y)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

计算数据的周期计数。显示周期计数的矩阵。

[c,hist,edges,rmm,idx] = rainflow(Y,fs);

T = array2table(c,VariableNames=["Count" "Range" "Mean" "Start" "End"])
T=7×5 table
    Count    Range    Mean    Start    End
    _____    _____    ____    _____    ___

     0.5       3      -0.5      0       1 
     0.5       4        -1      1       2 
       1       4         1      4       5 
     0.5       8         1      2       3 
     0.5       9       0.5      3       6 
     0.5       8         0      6       7 
     0.5       6         1      7       8

将周期计数直方图显示为应力范围的函数。

histogram(BinEdges=edges',BinCounts=sum(hist,2))
xlabel("Stress Range")
ylabel("Cycle Counts")

Figure contains an axes object. The axes object with xlabel Stress Range, ylabel Cycle Counts contains an object of type histogram.

使用不带输出参量的 rainflow 将周期直方图显示为周期均值和周期范围的函数。

rainflow(Y,fs)

Figure contains 2 axes objects. Axes object 1 with title Load Reversals, xlabel Time (secs), ylabel Amplitude contains an object of type line. Axes object 2 with title Rainflow Matrix Histogram, xlabel Cycle Range, ylabel Cycle Average contains an object of type histogram2.

打开实时脚本

生成类似于加载历史记录的信号，该信号由连接已知的非等间距反转的正弦半周期组成。该信号在 10 Hz 下采样 15 秒。绘制极值和信号。

fs = 10;

X = [0 1 3 4 5 6 8 10 13 15];
Y = [-2 1 -3 5 -1 3 -4 4 -2 6];

Z = [];
for k = 1:length(Y)-1
    x = X(k+1)-X(k);
    z = -(Y(k+1)-Y(k))*cos(pi*(0:1/fs:x-1/fs)/x)+Y(k+1)+Y(k);
    Z = [Z z/2];
end
Z = [Z Y(end)];

t = linspace(X(1),X(end),length(Z));
plot(X,Y,"o",t,Z)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

计算数据的周期计数。显示周期计数的矩阵。

[c,hist,edges,rmm,idx] = rainflow(Z,t);

TT = array2table(c,VariableNames=["Count" "Range" "Mean" "Start" "End"])
TT=7×5 table
    Count    Range    Mean    Start    End
    _____    _____    ____    _____    ___

     0.5       3      -0.5      0       1 
     0.5       4        -1      1       3 
       1       4         1      5       6 
     0.5       8         1      3       4 
       1       6         1     10      13 
     0.5       9       0.5      4       8 
     0.5      10         1      8      15

使用不带输出参量的 rainflow 将周期直方图显示为周期均值和周期范围的函数。

rainflow(Z,t)

Figure contains 2 axes objects. Axes object 1 with title Load Reversals, xlabel Time (secs), ylabel Amplitude contains an object of type line. Axes object 2 with title Rainflow Matrix Histogram, xlabel Cycle Range, ylabel Cycle Average contains an object of type histogram2.

打开实时脚本

生成一个以 100 Hz 的频率进行 100 秒采样的随机信号。将该信号及其时间信息存储在一个时间表中。

fs = 100;
t = seconds(0:1/fs:100-1/fs)';

x = randn(size(t));
TT = timetable(t,x);

显示该信号的反转和雨流矩阵。

rainflow(TT)

Figure contains 2 axes objects. Axes object 1 with title Load Reversals, xlabel Time, ylabel Amplitude contains an object of type line. Axes object 2 with title Rainflow Matrix Histogram, xlabel Cycle Range, ylabel Cycle Average contains an object of type histogram2.

打开实时脚本

生成一组类似于加载反转的极值。绘制数据图。

X = [-2 1 -3 5 -1 3 -4 4 -2]';

plot(X)
xlabel('Sample Index')  
ylabel('Stress')

Figure contains an axes object. The axes object with xlabel Sample Index, ylabel Stress contains an object of type line.

计算数据的周期计数。指定输入由已标识的极值组成。

[C,hist,edges] = rainflow(X,'ext');

将周期计数直方图显示为应力范围的函数。

histogram('BinEdges',edges','BinCounts',sum(hist,2))
xlabel('Stress Range')  
ylabel('Cycle Counts')

Figure contains an axes object. The axes object with xlabel Stress Range, ylabel Cycle Counts contains an object of type histogram.

使用不带输出参量的 rainflow 将周期直方图显示为周期均值和周期范围的函数。

rainflow(X,'ext')

Figure contains 2 axes objects. Axes object 1 with title Load Reversals, xlabel Samples, ylabel Amplitude contains an object of type line. Axes object 2 with title Rainflow Matrix Histogram, xlabel Cycle Range, ylabel Cycle Average contains an object of type histogram2.

输入参数

全部折叠

加载时间历史记录，指定为向量。x 必须具有有限值。

数据类型: single | double

采样率，指定为正实数标量。

数据类型: single | double

时间值，指定为向量、duration 数组或表示采样间时间间隔的 duration 标量。

示例: seconds(0:1/100:1) 是 duration 数组，表示在 100 Hz 下采样 1 秒。

数据类型: single | double | duration

加载时间历史记录，指定为时间表。xt 必须包含递增的有限行时间。时间表必须仅包含一个具有有限加载值的数值数据向量。

如果时间表有缺失或重复的时间点，您可以使用清理包含缺失、重复或不均匀时间的时间表中的提示进行修复。

示例: timetable(seconds(0:4)',rand(5,1)) 指定在 1 Hz 下采样 4 秒的随机变量。

数据类型: single | double

输出参量

全部折叠

周期计数，矩阵以形式返回。c 在其列中包含周期信息，顺序如下：计数、范围、均值、初始采样索引和最终采样索引。有关示例，请参阅算法。如果您指定采样率、时间间隔或时间值向量，则 c 的最后两列包含初始和最终周期时间。如果您以时间表为输入调用 rainflow，则最后两列以秒为单位表示初始和最终周期时间。

雨流矩阵。rm 的行对应周期范围，列对应周期均值。

直方图 bin 边界，以向量形式返回。rmr 和 rmm 分别包含 rm 的行和列的 bin 边界。

反转的线性索引，以向量形式返回。

算法

疲劳分析研究在承受应力周期性变化的物体中损伤如何累积。使物体断裂所需的周期次数取决于周期振幅。宽带输入激励包含不同振幅的周期，并且物体中滞后的存在导致一些周期嵌套在其他周期内，无论是完全还是部分嵌套。雨流计数估计作为周期振幅的函数的加载变化周期次数。

最初，rainflow 将加载历史记录转换为一个反转序列。反转是加载改变符号的局部最小值和最大值。该函数通过考虑序列的一个移动参考点 Z 和一个移动有序三点子集对周期进行计数，该子集具有以下特征：

  1. 第一个点和第二个点统称为 Y。

  2. 第二个点和第三个点统称为 X。

  3. 在 X 和 Y 中，各点按时间从早到晚排序，但它们不一定在反转序列中连续。

  4. X 的范围，由 r(X) 表示，是第一点的振幅与第二个点的振幅之差的绝对值。r(Y) 的定义类似。

rainflow 算法如下：

最后，该函数收集不同的周期和半周期，并对其范围、均值以及起始点和结束点进行制表。然后，此信息可用于生成周期直方图。

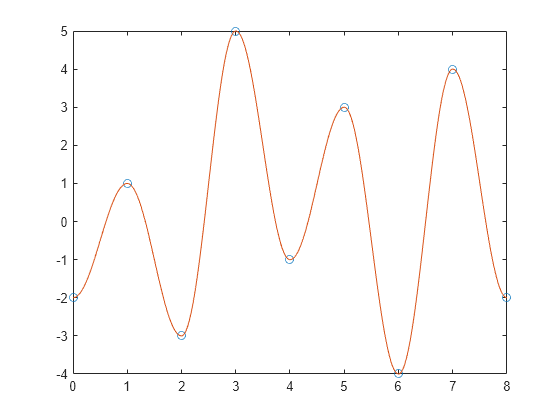
以如下反转序列为例：

步骤Z反转三个反转？Yr(Y)Xr(X)r(X) < r(Y)？Z 在 Y 中？动作
1AA、B、C是AB3BC4否是

  1. 将 AB 计为 ½ 个周期。

  2. 丢弃 A。

  3. 将 Z 设置为 B。

2BB、C否——————读取 D。
3BB、C、D是BC4CD8否是

  1. 将 BC 计为 ½ 个周期。

  2. 丢弃 B。

  3. 将 Z 设置为 C。

4CC、D否——————读取 E。
5CC、D、E是CD8DE6是—读取 F。
6CC、D、E、F是DE6EF4是—读取 G。
7CC、D、E、F、G是EF4FG7否否

  1. 将 EF 计为 1 个周期。

  2. 丢弃 E 和 F。

8CC、D、G是CD8DG9否是

  1. 将 CD 计为 ½ 个周期。

  2. 丢弃 C。

  3. 将 Z 设置为 D。

9DD、G否——————读取 H。
10DD、G、H是DG9GH8是—读取 J。
11DD、G、H、J是GH8HJ7是—读取 K。
12DD、G、H、J、K是HJ7JK4是—读取 L。
13DD、G、H、J、K、L是JK4KL3是—读取 M。
14DD、G、H、J、K、L、M是KL3LM5否否

  1. 将 KL 计为 1 个周期。

  2. 丢弃 K 和 L。

15DD、G、H、J、M是HJ7JM5是—读取 N。
16DD、G、H、J、M、N是JM5MN1是—读取 P。
17DD、G、H、J、M、N、P是MN1NP4否否

  1. 将 MN 计为 1 个周期。

  2. 丢弃 M 和 N。

18DD、G、H、J、P是HJ7JP9否否

  1. 将 HJ 计为 1 个周期。

  2. 丢弃 H 和 J。

19DD、G、P是DG9GP10否是

  1. 将 DG 计为 ½ 个周期。

  2. 丢弃 D。

  3. 将 Z 设置为 G。

20GG、P数据已用完——————

将 GP 计为 ½ 个周期。

现在收集结果。

周期计数范围均值起始结束
½3–0.5AB
½4–1BC
141EF
½81CD
13–0.5KL
112.5MN
170.5HJ
½90.5DG
½101GP

将此结果与对序列运行 rainflow 的结果进行比较：

q = rainflow([-2 1 -3 5 -1 3 -4 4 -3 1 -2 3 2 6])
q =

    0.5000    3.0000   -0.5000    1.0000    2.0000
    0.5000    4.0000   -1.0000    2.0000    3.0000
    1.0000    4.0000    1.0000    5.0000    6.0000
    0.5000    8.0000    1.0000    3.0000    4.0000
    1.0000    3.0000   -0.5000   10.0000   11.0000
    1.0000    1.0000    2.5000   12.0000   13.0000
    1.0000    7.0000    0.5000    8.0000    9.0000
    0.5000    9.0000    0.5000    4.0000    7.0000
    0.5000   10.0000    1.0000    7.0000   14.0000

参考

[1] ASTM E1049-85(2017), "Standard Practices for Cycle Counting in Fatigue Analysis." West Conshohocken, PA: ASTM International, 2017, https://www.astm.org/e1049-85r17.html.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

在 R2017b 中推出

另请参阅

| |

主题