thd
Total harmonic distortion
Syntax
Description
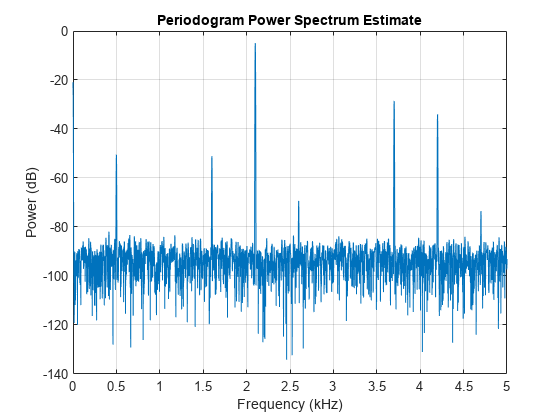
r = thd(x)x. The total harmonic distortion is determined from the
fundamental frequency and the first five harmonics using a modified periodogram
of the same length as the input signal. The modified periodogram uses a Kaiser
window with β = 38.
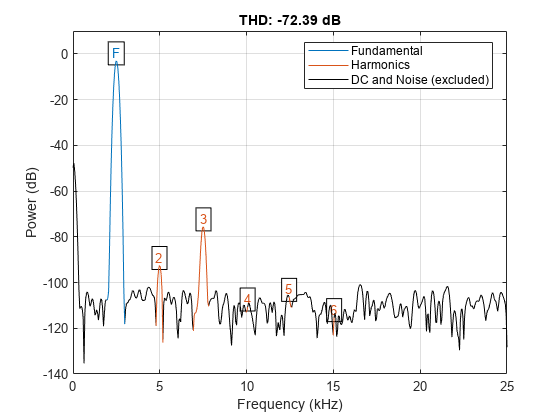
r = thd(___,"aliased")"omitaliases", then the function ignores any
harmonics of the fundamental frequency that lie beyond the Nyquist range.
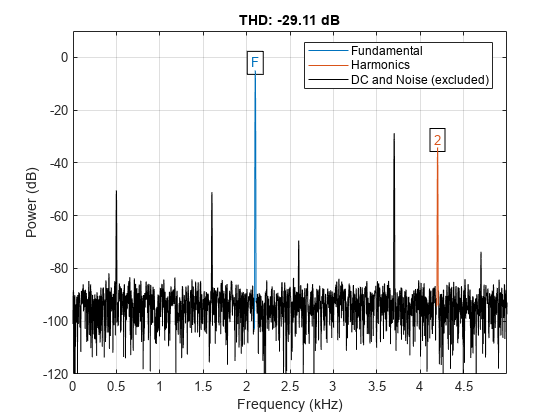
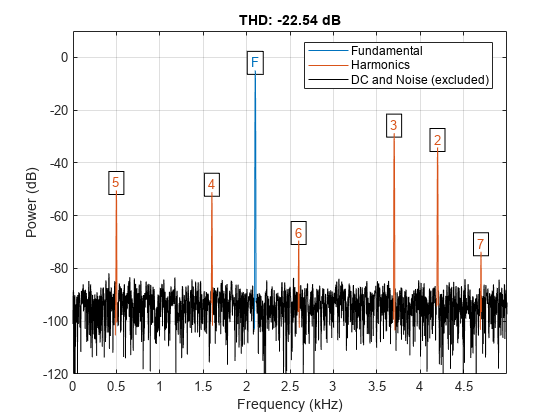
thd(___) with no output arguments
plots the spectrum of the signal and annotates the harmonics in the
current figure window. It uses different colors to draw the fundamental
component, the harmonics, and the DC level and noise. The THD appears
above the plot. The fundamental and harmonics are labeled. The DC
term is excluded from the measurement and is not labeled.