线性预测和自回归建模
此示例说明如何比较自回归建模和线性预测之间的关系。线性预测和自回归建模是两个不同的问题,但可以产生相同的数值结果。在这两种情况下,最终目标均为确定线性滤波器的参数。但是,每个问题中使用的滤波器不同。
简介
在线性预测的情况下,目的是确定一个 FIR 滤波器,以便能够基于过去采样的线性组合最优地预测自回归过程的将来采样。实际自回归信号和预测信号之间的差异称为预测误差。理想情况下,此误差为白噪声。
对于自回归建模的情况,目的是确定一个全极点 IIR 滤波器,当使用白噪声刺激该滤波器时,它产生与我们尝试建模的自回归过程具有相同统计量的信号。
使用以白噪声为输入的全极点滤波器生成 AR 信号
在此处,我们使用 LPC 函数和 FIR 滤波器来简单地得出参数,我们将使用这些参数来创建要处理的自回归信号。FIR1 和 LPC 的使用在此处并不重要。例如,我们可以用 [1 1/2 1/3 1/4 1/5 1/6 1/7 1/8] 这样简单的项代替 d,用 1e-6 这样的项代替 p0。但是,此滤波器的形状更好,因此我们使用它。
b = fir1(1024, .5); [d,p0] = lpc(b,7);
为了生成自回归信号,我们将使用方差为 p0 的高斯白噪声刺激全极点滤波器。请注意,为了获得方差 p0,我们必须在噪声生成器中使用 SQRT(p0) 作为 'gain' 项。
rng(0,'twister'); % Allow reproduction of exact experiment u = sqrt(p0)*randn(8192,1); % White Gaussian noise with variance p0
我们现在使用高斯白噪声信号和全极点滤波器来生成 AR 信号。
x = filter(1,d,u);
使用尤尔-沃克方法从信号中求得 AR 模型
通过求解尤尔-沃克方程,我们可以确定一个全极点滤波器的参数,当用白噪声刺激时,该滤波器将产生统计量与给定信号 x 的统计量相匹配的 AR 信号。同样,这也称为自回归建模。为了求解尤尔-沃克方程,需要估计 x 的自相关函数。然后使用莱文森算法以高效方式求解尤尔-沃克方程。ARYULE 函数可以完成所有这些工作。
[d1,p1] = aryule(x,7);
比较 AR 模型与 AR 信号
现在,我们想计算刚刚用于 AR 信号 x 建模的全极点滤波器的频率响应。众所周知,当此滤波器受高斯白噪声刺激时,它输出的功率谱密度由其频率响应的幅值平方乘以白噪声输入的方差给出。计算此输出功率谱密度的一种方法是使用 FREQZ,如下所示:
[H1,w1] = freqz(sqrt(p1),d1);
为了了解我们对自回归信号 x 的建模情况,我们将以下两者进行叠加:使用 FREQZ 计算的模型输出的功率谱密度,以及使用 PERIODOGRAM 计算的 x 的功率谱密度估计值。请注意,周期图按 2*pi 缩放,并且是单侧图。为了进行比较,我们需要对此进行调整。
periodogram(x) hold on hp = plot(w1/pi,20*log10(2*abs(H1)/(2*pi)),'r'); % Scale to make one-sided PSD hp.LineWidth = 2; xlabel('Normalized frequency (\times \pi rad/sample)') ylabel('One-sided PSD (dB/rad/sample)') legend('PSD estimate of x','PSD of model output')

使用 LPC 执行线性预测
我们现在看看线性预测问题。在此处,我们尝试确定一个 FIR 预测滤波器。我们用 LPC 来完成这项工作,但需要对 LPC 的结果稍加解释。LPC 返回整个白化滤波器 A(z) 的系数,此滤波器接受自回归信号 x 作为输入,并将预测误差作为输出返回。然而,A(z) 中嵌入了预测滤波器,其形式为 B(z) = 1- A(z),其中 B(z) 是预测滤波器。请注意,用 LPC 计算的系数和误差方差与用 ARYULE 计算的系数和误差方差基本相同,但其解释不同。
[d2,p2] = lpc(x,7); [d1.',d2.']
ans = 8×2
1.0000 1.0000
-3.5245 -3.5245
6.9470 6.9470
-9.2899 -9.2899
8.9224 8.9224
-6.1349 -6.1349
2.8299 2.8299
-0.6997 -0.6997
我们现在如上所述从 A(z) 中提取 B(z),以使用 FIR 线性预测变量滤波器来基于过去值的线性组合获得自回归信号将来值的估计值。
xh = filter(-d2(2:end),1,x);
比较实际信号和预测信号
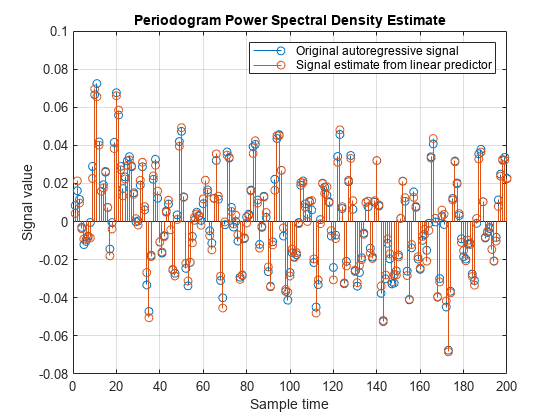
为了了解我们对 7 抽头 FIR 预测滤波器所做的工作,我们绘制原始自回归信号的 200 个采样以及基于线性预测变量生成的信号估计值,同时考虑预测滤波器中的单采样延迟。
cla stem([x(2:end),xh(1:end-1)]) xlabel('Sample time') ylabel('Signal value') legend('Original autoregressive signal','Signal estimate from linear predictor') axis([0 200 -0.08 0.1])
比较预测误差
预测误差功率(方差)作为 LPC 的第二个输出返回。其值(理论上)与在 AR 建模问题 (p1) 中驱动全极点滤波器的白噪声的方差相同。估计方差的另一种方法是基于预测误差本身来估计:
p3 = norm(x(2:end)-xh(1:end-1),2)^2/(length(x)-1);
以下所有值在理论上是相同的。差异是此处的各种计算和逼近误差造成的。
[p0 p1 p2 p3]
ans = 1×4
10-5 ×
0.5127 0.5305 0.5305 0.5068