仿真系统和风力涡轮叶片的模态分析
此示例说明如何根据试验数据估计频率响应函数 (FRF) 和模态参数。第一部分说明仿真试验,该试验用一系列锤击来激励一个三自由度 (3DOF) 系统,并记录由此产生的位移。同时还估计该结构的三个模态的频率响应函数、固有频率、阻尼比和模态振形向量。第二个部分根据来自风力涡轮叶片试验的频率响应函数估计值来估计模态振形向量。并对涡轮叶测量配置和产生的模态振形进行可视化。此示例需要 System Identification Toolbox™。
仿真波束的固有频率和阻尼
单输入/单输出锤激励
通过一系列锤击激励 3DOF 系统,使用传感器记录由此产生的位移。系统呈现了比例阻尼特性,其阻尼矩阵可表示为质量矩阵和刚度矩阵的线性组合。
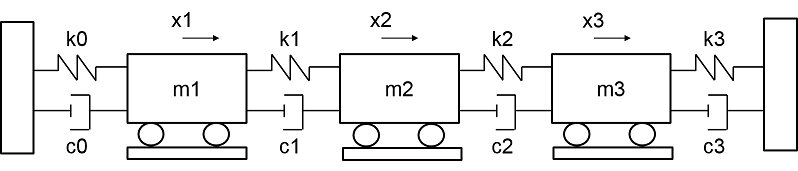
导入两组测量数据,包括激励信号、响应信号、时间信号和真实值频率响应函数。第一组响应信号 Y1 测量第一个质量的位移,第二组 Y2 测量第二个质量的位移。每个激励信号由十个串联的锤击组成,每个响应信号包含对应的位移。每个锤击信号的持续时间为 2.53 秒。激励信号和响应信号中存在加性噪声。可视化第一次测量的第一个激励和响应通道。
[t,fs,X1,X2,Y1,Y2,f0,H0] = helperImportModalData(); X0 = X1(:,1); Y0 = Y1(:,1); helperPlotModalAnalysisExample([t' X0 Y0]);

计算并绘制第一个激励和响应通道的动柔度 FRF,动柔度是作用力所产生的位移的测度 [1]。默认情况下,通过求加窗后各分段的频谱平均值来计算 FRF。由于每次锤击激励在下一次激励之前会明显衰减,因此可以使用矩形窗。将传感器指定为位移。
winLen = 2.5275*fs; % window length in samples modalfrf(X0,Y0,fs,winLen,'Sensor','dis')
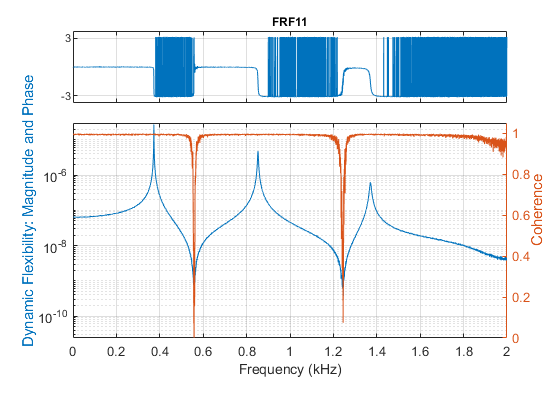
使用默认的 'H1' 估计量估计的 FRF 包含测量频带中的三个显著峰值,对应于三种柔性振动模态。在这些峰值附近,相干性接近 1,在反共振区域,相干性较低,反共振区域中响应测量的信噪比较低。接近 1 的相干性表示估计质量高。在噪声仅存在于输出测量值中的情况下,'H1' 估计值是最佳的;在加性噪声仅存在于输入端的情况下,'H2' 估计值是最佳的 [2]。为此 FRF 计算 'H1' 和 'H2' 估计值。
[FRF1,f1] = modalfrf(X0,Y0,fs,winLen,'Sensor','dis'); % Calculate FRF (H1) [FRF2,f2] = modalfrf(X0,Y0,fs,winLen,'Sensor','dis','Estimator','H2');
当存在显著的测量噪声或激励较弱时,参数化方法可以提供额外的选项,用于从数据中准确提取 FRF。'subspace' 方法首先对数据进行状态空间模型拟合 [3],然后计算其频率响应函数。配置状态空间估计时可以指定状态空间模型的阶(等于极点数)和馈通的存在与否。
[FRF3,f3] = modalfrf(X0,Y0,fs,winLen,'Sensor','dis','Estimator','subspace','Feedthrough',true);
此处,我们通过拟合包含馈通项且具有 1:10 范围内的最优阶的状态空间模型来估计 FRF3。将使用 'H1'、'H2' 和 'subspace' 方法估计的 FRF 与理论 FRF 进行比较。
helperPlotModalAnalysisExample(f1,FRF1,f2,FRF2,f3,FRF3,f0,H0);

该估计量在响应峰值附近表现相对较好,而 'H2' 估计量会高估反共振区域的响应。相干性不受所选估计量的影响。
接下来,使用峰值拾取法估计每个模态的固有频率。峰值拾取法是一种简单快速的识别 FRF 峰值的方法。它是一种局部方法,因为每个估计值都是由单个频率响应函数生成的。它也是一种单自由度 (SDOF) 方法,因为每个模态的峰值是独立考虑的。因此,每个 FRF 都会生成一组模态参数。根据前面的图,指定 200 至 1600 Hz 的频率范围,其中包含三个峰值。
fn = modalfit(FRF1,f1,fs,3,'FitMethod','PP','FreqRange',[200 1600])
fn =
1.0e+03 *
0.3727
0.8525
1.3707
固有频率约为 373、853 和 1371 Hz。绘制重新构造的 FRF 图,并使用 modalfit 将其与测量的数据进行比较。该 FRF 是使用从频率响应函数矩阵 FRF1 估计的模态参数重新构造的。在不带输出参量的情况下再次调用 modalfit,以生成包含重新构造的 FRF 的图。
modalfit(FRF1,f1,fs,3,'FitMethod','PP','FreqRange',[200 1600])
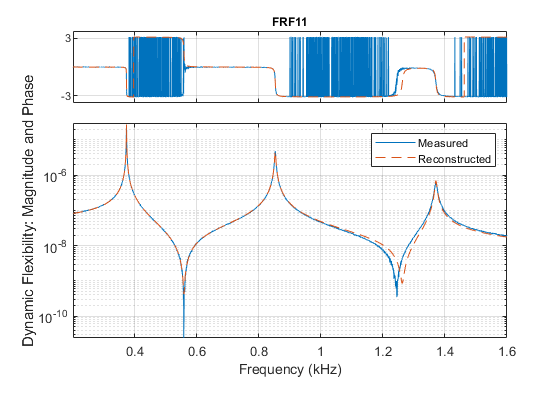
重新构造的 FRF 与测量的第一个激励和响应通道的 FRF 一致。在下一节中,将考虑另外两个激励位置。
动力锤激励
使用默认的 'H1' 估计量计算并绘制所有三个传感器响应的 FRF。指定测量类型为 'rovinginput',因为我们有动力锤激励。
modalfrf(X1,Y1,fs,winLen,'Sensor','dis','Measurement','rovinginput')

在前一节中,我们是从单个 FRF 计算出一组模态参数。现在,使用最小二乘复指数 (LSCE) 算法估计模态参数。LSCE 和 LSRF 算法通过同时分析多个响应信号生成一组模态参数。这些是全局多自由度 (MDOF) 方法,因为所有模态的参数都是基于多个频率响应函数同时估计的。
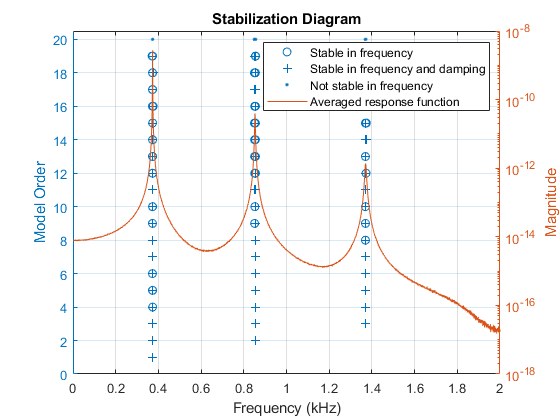
LSCE 算法生成的是计算模态,这些模态在结构中并不实际存在。可以使用稳定图通过检查模态数增加时极点的稳定性来识别物理模态。物理模态的固有频率和阻尼比倾向于保持在同一位置,即“保持稳定”。创建一个稳定图,并输出频率稳定的极点的固有频率。
[FRF,f] = modalfrf(X1,Y1,fs,winLen,'Sensor','dis','Measurement','rovinginput'); fn = modalsd(FRF,f,fs,'MaxModes',20, 'FitMethod', 'lsce'); % Identify physical modes

默认情况下,如果极点的固有频率变化小于 1%,则归类为频率稳定极点。频率稳定极点可进一步归类为阻尼比变化小于 5% 的阻尼稳定极点。这两个条件可以调整为不同的值。根据稳定极点的位置,选择 373、852.5 和 1371 Hz 的固有频率。这些频率包含在 modalsd 的输出 fn 中,其中还包含其他频率稳定极点的固有频率。为了使用 LSCE 算法生成良好的模态参数估计值,通常需要比物理存在的模态数量更高的模型阶数。在本例中,具有四个模态的模型阶数显示了三个稳定极点。我们感兴趣的频率出现在 fn 的第四行的前三列中。
physFreq = fn(4,[1 2 3]);
估计固有频率和阻尼,绘制重新构造的以及测量的 FRF。指定根据稳定图确定的四个模态和物理频率 'PhysFreq'。modalfit 仅返回指定模态的模态参数。
modalfit(FRF,f,fs,4,'PhysFreq',physFreq)

[fn1,dr1] = modalfit(FRF,f,fs,4,'PhysFreq',physFreq)
fn1 =
1.0e+03 *
0.3727
0.8525
1.3706
dr1 =
0.0008
0.0018
0.0029
接下来,计算 FRF 并绘制第二组锤击的稳定图,传感器位于不同位置。将频率稳定条件改为 0.1%,阻尼稳定条件改为 2.5%。
[FRF,f] = modalfrf(X2,Y2,fs,winLen,'Sensor','dis','Measurement','rovinginput'); fn = modalsd(FRF,f,fs,'MaxModes',20,'SCriteria',[0.001 0.025]);
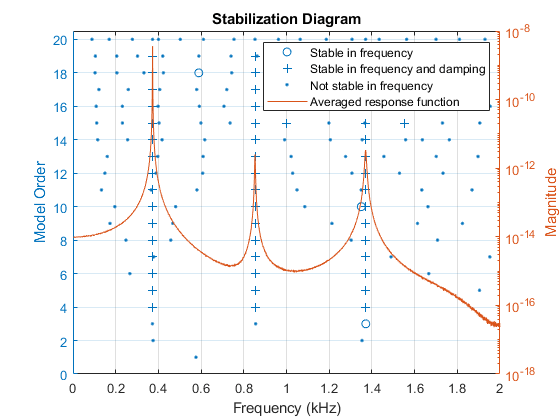
根据更严格的条件,大多数极点归类为频率不稳定。频率和阻尼稳定的极点与平均 FRF 紧密一致,表明它们存在于所测量数据中。
physFreq = fn(4,[1 2 3]);
提取这组测量的模态参数,并与第一组测量的模态参数进行比较。指定驱动点 FRF 的索引,对应于激励和响应测量一致的位置。固有频率差异低于百分之一,阻尼比差异低于百分之四,表明模态参数在这两次测量之间是一致的。
[fn2,dr2] = modalfit(FRF,f,fs,4,'PhysFreq',physFreq,'DriveIndex',[1 2])
fn2 =
1.0e+03 *
0.3727
0.8525
1.3705
dr2 =
0.0008
0.0018
0.0029
Tdiff2 = table((fn1-fn2)./fn1,(dr1-dr2)./dr1,'VariableNames',{'diffFrequency','diffDamping'})
Tdiff2 =
3×2 table
diffFrequency diffDamping
_____________ ___________
2.9972e-06 -0.031648
-5.9335e-06 -0.0099076
1.965e-05 0.0001186
当 FRF 存在测量噪声或 FRF 显示高模态密度时,可使用参数化方法来估计模态参数,这是峰值拾取和 LSCE 方法的一个实用替代方法。最小二乘有理函数 (LSRF) 方法对多输入多输出 FRF 进行公分母传递函数拟合,从而获得模态参数的单一全局估计值 [4]。使用 LSRF 方法的过程与 LSCE 相似。您可以使用稳定图来识别平稳模态,并提取与识别的物理频率对应的模态参数。
[FRF,f] = modalfrf(X1,Y1,fs,winLen,'Sensor','dis','Measurement','rovinginput'); fn = modalsd(FRF,f,fs,'MaxModes',20, 'FitMethod', 'lsrf'); % Identify physical modes using lsfr physFreq = fn(4,[1 2 3]); [fn3,dr3] = modalfit(FRF,f,fs,4,'PhysFreq',physFreq,'DriveIndex',[1 2],'FitMethod','lsrf')
fn3 =
372.6832
372.9275
852.4986
dr3 =
0.0008
0.0003
0.0018
Tdiff3 = table((fn1-fn3)./fn1,(dr1-dr3)./dr1,'VariableNames',{'diffFrequency','diffDamping'})
Tdiff3 =
3×2 table
diffFrequency diffDamping
_____________ ___________
-7.8599e-06 0.007982
0.56255 0.83086
0.37799 0.37626
关于参数化方法的最后一点:FRF 估计方法 ('subspace') 和模态参数估计方法 ('lsrf') 类似于 System Identification Toolbox 中用于对时域信号或频率响应函数进行动态模型拟合的那些方法。如果您有此工具箱,您可以使用 tfest 和 ssest 等命令来识别可拟合您的数据的模型。您可以使用 compare 和 resid 命令评估已识别模型的质量。一旦验证了模型的质量,就可以使用它们来提取模态参数。这可以使用状态空间估计量进行简单的展示。
Ts = 1/fs; % sample time % Create a data object to be used for model estimation. EstimationData = iddata(Y0(1:1000), X0(1:1000), 1/fs); % Create a data object to be used for model validation ValidationData = iddata(Y0(1001:2000), X0(1001:2000), 1/fs);
识别一个包含馈通项的 6 阶连续时间状态空间模型。
sys = ssest(EstimationData, 6, 'Feedthrough', true)
sys =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2 x3 x4 x5 x6
x1 4.041 1765 -149.8 1880 -49.64 -358
x2 -1764 -0.3434 2197 -232.5 438.3 128.4
x3 152.4 -2198 2.839 4715 -255.9 -547.5
x4 -1880 228.2 -4714 -15.91 1216 28.79
x5 59.42 -440.9 275.5 -1217 35.03 -8508
x6 363.7 -120.2 545.4 44.02 8508 -92.47
B =
u1
x1 -0.2777
x2 -0.6085
x3 0.07123
x4 -3.658
x5 -0.04771
x6 7.642
C =
x1 x2 x3 x4 x5 x6
y1 -4.46e-05 -5.315e-06 -7.46e-06 -1.641e-05 -2.964e-06 5.871e-06
D =
u1
y1 7.997e-09
K =
y1
x1 -3.513e+07
x2 -3.244e+06
x3 -3.598e+07
x4 -1.059e+07
x5 -1.724e+08
x6 -7.521e+06
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: yes
Disturbance component: estimate
Number of free coefficients: 55
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on time domain data "EstimationData".
Fit to estimation data: 99.26% (prediction focus)
FPE: 1.355e-16, MSE: 1.304e-16
通过检查模型与验证数据的拟合程度来评估模型的质量。
clf
compare(ValidationData, sys) % plot shows good fit

使用模型 sys 计算模态参数。
[fn4, dr4] = modalfit(sys, f, 3);
风力涡轮叶片的模态振形向量
了解风力涡轮叶片的动态行为对于优化运行效率和预测叶片故障非常重要。本部分分析风力涡轮叶片的试验模态分析数据,并可视化叶片的模态振形。这里我们通过在 20 个位置锤击来激励涡轮叶片,并使用参考加速度计在位置 18 处测量响应。叶片的基部安装了一个铝制模块,叶片受到了垂直于叶片平面部分的襟翼方向作用力的激励。每个位置都采集了对应的 FRF。FRF 数据由马萨诸塞州洛厄尔大学的结构动态和声学系统实验室提供。首先,可视化测量位置的空间布局。

加载并绘制位置 18 和 20 的风力涡轮叶片 FRF 估计值。放大前几个峰值。
[FRF,f,fs] = helperImportModalData(); helperPlotModalAnalysisExample(FRF,f,[18 20]);

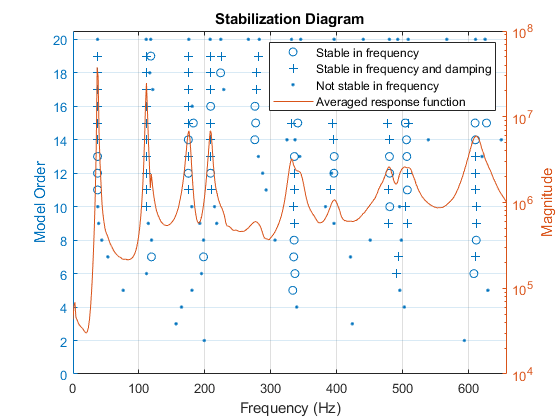
前两个模态在 37 Hz 和 111 Hz 附近出现峰值。绘制稳定图以估计固有频率。模型阶数为 14 时返回的前两个值在频率和阻尼比方面是稳定的。
fn = modalsd(FRF,f,fs,'MaxModes',20);
physFreq = fn(14,[1 2]);
接下来,使用 modalfit 提取前两个模态的模态振形。根据前面的图,将拟合限制在 0 至 250 Hz 的频率范围内。
[~,~,ms] = modalfit(FRF,f,fs,14,'PhysFreq',physFreq,'FreqRange',[0 250]);
模态振形量化了结构的每个模态在每个位置上的振幅。为了估计模态振形向量,需要用到频率响应函数矩阵的一行或一列。实际上,这意味着要么在结构的每个测量位置都需要一个激励(在本例中是一个动力锤),要么在每个位置都需要进行响应测量。模态振形可以通过查看 FRF 的虚部来可视化。绘制叶片一侧的各位置的 FRF 矩阵虚部的瀑布图。将频率范围限制为最大 150 Hz 以检查前两个模态。图的峰值表示模态振形。
measlocs = [3 6 9 11 13 15 17 19 20]; % Measurement locations on blade edge
helperPlotModalAnalysisExample(FRF,f,measlocs,150);
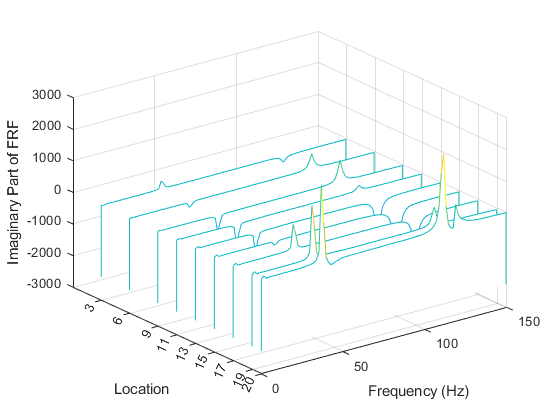
图中由峰轮廓指示的振形表示叶片的第一和第二个弯矩。接下来,绘制相同测量位置的模态振形向量的幅值。
helperPlotModalAnalysisExample(ms,measlocs);
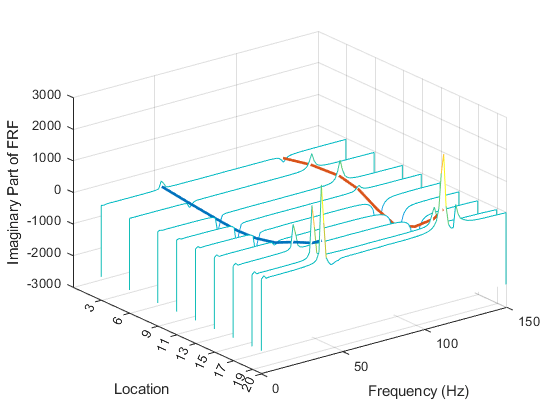
虽然振幅的缩放不同(模态振形向量缩放到单位模态 A),但模态振形轮廓的形状是一致的。第一个模态的振形具有一个大的叶尖位移和两个节点,节点振幅为零。第二个模态也具有一个大的叶尖位移,并且具有三个节点。
总结
此示例分析和比较了由动力锤激励的 3DOF 系统的仿真模态分析数据集。它使用稳定图以及 LSCE 和 LSRF 算法估算了固有频率和阻尼。两组测量的模态参数是一致的。在另一个案例中,我们使用了 FRF 矩阵的虚部和模态振形向量对风力涡轮叶片的模态振形进行了可视化。
致谢
感谢马萨诸塞州洛厄尔大学结构动力学和声学系统实验室的 Peter Avitabile 博士为收集风力涡轮叶片试验数据提供的便利。
参考资料
[1] Brandt, Anders.Noise and Vibration Analysis:Signal Analysis and Experimental Procedures.Chichester, UK:John Wiley and Sons, 2011.
[2] Vold, Håvard, John Crowley, and G. Thomas Rocklin."New Ways of Estimating Frequency Response Functions."Sound and Vibration.Vol. 18, November 1984, pp. 34-38.
[3] Peter Van Overschee and Bart De Moor."N4SID:Subspace Algorithms for the Identification of Combined Deterministic-Stochastic Systems."Automatica.Vol. 30, January 1994, pp. 75-93.
[4] Ozdemir, A. A., and S. Gumussoy."Transfer Function Estimation in System Identification Toolbox via Vector Fitting."Proceedings of the 20th World Congress of the International Federation of Automatic Control.Toulouse, France, July 2017.