从信号中去除 60 Hz 杂声
美国和其他几个国家/地区的交流电以 60 Hz 的频率振荡。这些振荡通常会破坏测量结果,必须将其减去。
在存在 60 Hz 电力线噪声的情况下,研究模拟仪器的输入的开环电压。电压采样频率为 1 kHz。
load openloop60hertz, openLoop = openLoopVoltage; Fs = 1000; t = (0:length(openLoop)-1)/Fs; plot(t,openLoop) ylabel('Voltage (V)') xlabel('Time (s)') title('Open-Loop Voltage with 60 Hz Noise') grid
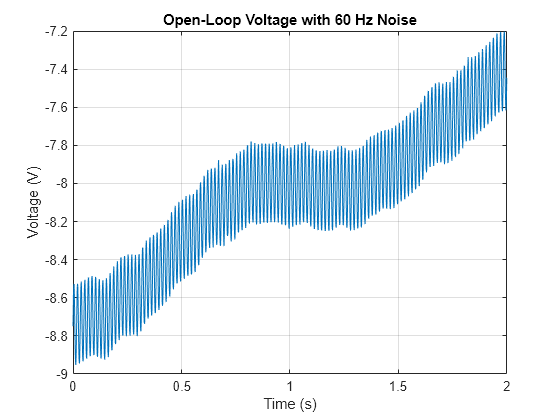
使用巴特沃斯陷波滤波器消除 60 Hz 噪声。使用 designfilt 设计该滤波器。陷波的宽度定义为 59 至 61 Hz 的频率区间。滤波器至少去除该范围内频率分量的一半功率。
d = designfilt('bandstopiir','FilterOrder',2, ... 'HalfPowerFrequency1',59,'HalfPowerFrequency2',61, ... 'DesignMethod','butter','SampleRate',Fs);
绘制滤波器的频率响应。请注意,此陷波滤波器提供高达 45 dB 的衰减。
freqz(d,[],Fs)

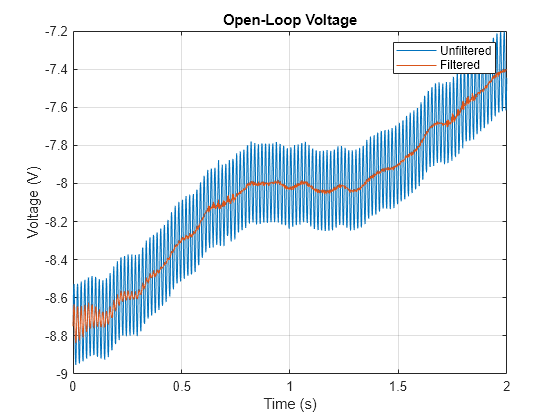
用 filtfilt 对信号进行滤波,以补偿滤波器延迟。注意振荡是如何显著减少的。
buttLoop = filtfilt(d,openLoop); plot(t,openLoop,t,buttLoop) ylabel('Voltage (V)') xlabel('Time (s)') title('Open-Loop Voltage') legend('Unfiltered','Filtered') grid
使用周期图可以看到 60 Hz 的“峰值”已去除。
[popen,fopen] = periodogram(openLoop,[],[],Fs); [pbutt,fbutt] = periodogram(buttLoop,[],[],Fs); plot(fopen,20*log10(abs(popen)),fbutt,20*log10(abs(pbutt)),'--') ylabel('Power/frequency (dB/Hz)') xlabel('Frequency (Hz)') title('Power Spectrum') legend('Unfiltered','Filtered') grid

另请参阅
designfilt | filtfilt | periodogram