filtfilt

零相位数字滤波

全页折叠

语法

y = filtfilt(b,a,x)

y = filtfilt(sos,g,x)

y = filtfilt(d,x)

y = filtfilt(B,A,x,"ctf")

y = filtfilt({B,A,g},x)

说明

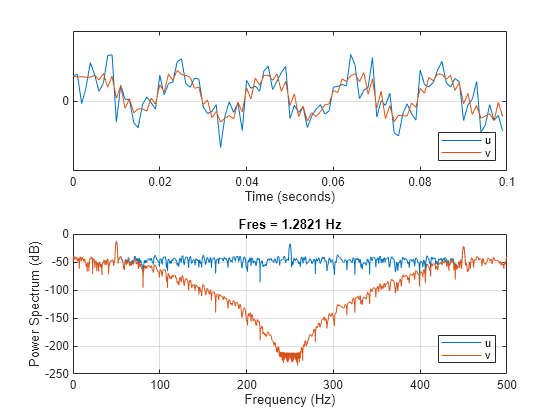
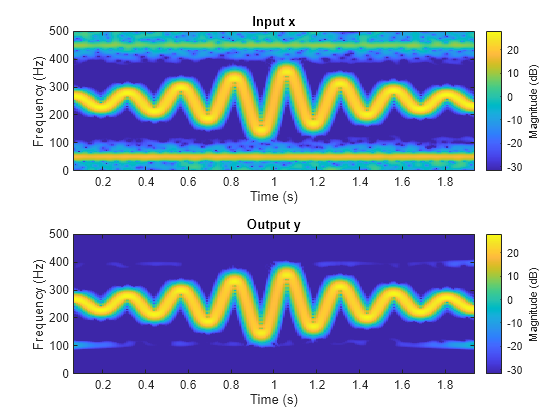
y = filtfilt(b,a,x) 通过正向和反向处理输入数据 x 来执行零相位数字滤波。在对数据进行正向滤波后，该函数会匹配初始条件以最大限度地减少启动和结束时的瞬变，反转滤波后的序列，并让反转后的序列再次通过滤波器。结果具有以下特征：

零相位失真
滤波器传递函数等于原始滤波器传递函数的平方幅值
滤波器阶数是由 b 和 a 指定的滤波器阶数的两倍

filtfilt 实现了 Gustafsson 提出的算法 [1]。

不要将 filtfilt 与微分器和希尔伯特 FIR 滤波器结合使用，因为这些滤波器的运算在很大程度上取决于它们的相位响应。

示例

y = filtfilt(sos,g,x) 使用由矩阵 sos 和尺度值 g 表示的二阶节 (biquad) 滤波器对输入数据 x 进行零相位滤波。

y = filtfilt(d,x) 使用数字滤波器 d 对输入数据 x 进行零相位滤波。使用 designfilt 根据频率响应设定生成 d。

示例

y = filtfilt(B,A,x,"ctf") 零相位使用由分子系数和分母系数（分别为 B 和 A）定义的Cascaded Transfer Functions (CTF) 对输入数据 x 进行滤波。 (自 R2024b 起)

注意

当您将 A 指定为标量或向量时，指定 "ctf" 选项以将具有六列的 CTF 分子矩阵 B 与二阶节矩阵输入 sos 区分开来。

示例

y = filtfilt({B,A,g},x) 在输入数据 x 的滤波中包括滤波器标量值 g。 (自 R2024b 起)

示例

全部折叠

心电图波形的零相位滤波

打开实时脚本

零相位滤波有助于将滤波后的时间波形中的特征准确地保留在它们在未经滤波的信号中出现的位置。

对合成心电图 (ECG) 波形进行零相位滤波。生成波形的函数在示例的末尾。QRS 复波是 ECG 的一个重要特征。如下图所示，它在时间点 160 左右开始。

wform = ecg(500);

plot(wform)
axis([0 500 -1.25 1.25])
text(155,-0.4,"Q")
text(180,1.1,"R")
text(205,-1,"S")

Figure contains an axes object. The axes object contains 4 objects of type line, text.

用加性噪声损坏 ECG。重置随机数生成器以获得可重现的结果。构造一个低通 FIR 等波纹滤波器，并使用零相位滤波和传统滤波对含噪波形进行滤波。

rng("default")

x = wform' + 0.25*randn(500,1);
d = designfilt("lowpassfir", ...
    PassbandFrequency=0.15,StopbandFrequency=0.2, ...
    PassbandRipple=1,StopbandAttenuation=60, ...
    DesignMethod="equiripple");
y = filtfilt(d,x);
y1 = filter(d,x);

tiledlayout("flow")
nexttile
plot([y y1])
title("Filtered Waveforms")
legend(["Zero-phase Filtering" "Conventional Filtering"])

nexttile
plot(wform)
title("Original Waveform")

Figure contains 2 axes objects. Axes object 1 with title Filtered Waveforms contains 2 objects of type line. These objects represent Zero-phase Filtering, Conventional Filtering. Axes object 2 with title Original Waveform contains an object of type line.

零相位滤波可减少信号中的噪声，并在原始信号中出现 QRS 复波的同时保留该复波。传统滤波可减少信号中的噪声，但会使 QRS 复波延迟。

使用巴特沃斯二阶节滤波器重复进行滤波。

d1 = designfilt("lowpassiir",FilterOrder=12, ...
    HalfPowerFrequency=0.15,DesignMethod="butter");
y = filtfilt(d1,x);

figure
plot(x)
hold on
plot(y,LineWidth=3)
hold off
legend(["Noisy ECG" "Zero-Phase Filtering"])

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Noisy ECG, Zero-Phase Filtering.

此函数生成 ECG 波形。

function x = ecg(L)
%ECG Electrocardiogram (ECG) signal generator.
%   ECG(L) generates a piecewise linear ECG signal of length L.
%
%   EXAMPLE:
%   x = ecg(500).';
%   y = sgolayfilt(x,0,3); % Typical values are: d=0 and F=3,5,9, etc. 
%   y5 = sgolayfilt(x,0,5); 
%   y15 = sgolayfilt(x,0,15); 
%   plot(1:length(x),[x y y5 y15]);

%   Copyright 1988-2002 The MathWorks, Inc.

a0 = [0,1,40,1,0,-34,118,-99,0,2,21,2,0,0,0]; % Template
d0 = [0,27,59,91,131,141,163,185,195,275,307,339,357,390,440];
a = a0/max(a0);
d = round(d0*L/d0(15)); % Scale them to fit in length L
d(15)=L;

for i=1:14
       m = d(i):d(i+1)-1;
       slope = (a(i+1)-a(i))/(d(i+1)-d(i));
       x(m+1) = a(i)+slope*(m-d(i));
end

end

线性啁啾的零相位级联滤波

自 R2024b 起

打开实时脚本

使用级联传递函数执行零相位滤波。

设计一个椭圆滤波器，通带波纹和阻带衰减分别为 0.1 dB 和 40 dB。指定采样率为 2000 Hz。绘制滤波器的频率响应。

Fs = 2000;
[B,A] = ellip(20,0.1,40,[0.3 0.7],"ctf");
freqz(B,A,2048,Fs,"ctf")

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Frequency (kHz), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Frequency (kHz), ylabel Magnitude (dB) contains an object of type line.

对线性扫频啁啾信号进行滤波，其中奈奎斯特频率出现在一秒处。比较输入和输出信号的频谱。

t = 0:1/Fs:1;
x = chirp(t,0,t(end),Fs/2)';
y = filtfilt(B,A,x,"ctf");
pspectrum([x y],Fs,Leakage=1,FrequencyResolution=1)

Figure contains an axes object. The axes object with title Fres = 1 Hz, xlabel Frequency (kHz), ylabel Power Spectrum (dB) contains 2 objects of type line.

从振荡信号中滤除正弦波伪影

自 R2024b 起

打开实时脚本

用传递函数零相位滤波重新生成含噪正弦波伪影。使用 CTF 和尺度值对振荡信号进行滤波。

创建一个由正态分布噪声和三个正弦波形组成的信号 u。采样率为 1 kHz。

rng("default")
Fs = 1e3;
ts = (0:1/Fs:2)';

a0 = [3 2 1];
f0 = [0.1 0.5 0.9]*Fs/2;
p0 = [0 pi/4 pi/2];

u = 0.1*randn(size(ts)) + 0.1*sin(2*pi*f0.*ts+p0)*a0';

通过使用三阶巴特沃斯带阻数字滤波器对 n0 进行滤波，重新生成含噪正弦波伪影，并创建信号 v。

[b,a] = butter(3,[0.15 0.85],"stop");
v = filtfilt(b,a,u);

比较 u 和 v。注意两个信号同相。

tiledlayout("flow")
nexttile
strips([u(ts<0.1) v(ts<0.1)],0.1,Fs)
legend(["u" "v"],Location="southeast")
xlabel("Time (seconds)")
nexttile
pspectrum([u v],Fs)
legend(["u" "v"],Location="southeast")

Figure contains 2 axes objects. Axes object 1 with xlabel Time (seconds) contains 2 objects of type line. These objects represent u, v. Axes object 2 with title Fres = 1.2821 Hz, xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 2 objects of type line. These objects represent u, v.

生成一个电压控制的振荡信号 x。添加由信号 v 表示的含噪正弦波伪影。

vo = exp(-2*abs(ts-1)).*sin(8*pi*ts);
x = vco(vo,[0.25 0.75]*Fs/2,Fs) + v;

用 24 阶切比雪夫 II 型滤波器对信号 x 进行滤波。使用 CTF 格式和尺度值 (B,A,g)。

[B,A,g] = cheby2(24,50,[0.2 0.8],"ctf");
y = filtfilt({B,A,g},x);

比较短时傅里叶变换的幅值平方。观察幅值在阻带处急剧下降。

tiledlayout("flow")
nexttile
stft(x,Fs,Window=bohmanwin(128),OverlapLength=120, ...
    FFTLength=512,FrequencyRange="onesided")
title("Input x")
nexttile
stft(y,Fs,Window=bohmanwin(128),OverlapLength=120, ...
    FFTLength=512,FrequencyRange="onesided")
title("Output y")

Figure contains 2 axes objects. Axes object 1 with title Input x, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image. Axes object 2 with title Output y, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

输入参数

全部折叠

`b`, `a` — 传递函数系数
向量

传递函数系数，指定为向量。如果使用全极点滤波器，请将 b 设置为 1。如果使用全零点 (FIR) 滤波器，请将 a 设置为 1。

示例: b = [1 3 3 1]/6 和 a = [3 0 1 0]/3 用于指定一个归一化 3 dB 频率为 0.5π 弧度/采样点的三阶巴特沃斯滤波器。

数据类型: double | single

`x` — 输入信号
向量 | 矩阵 | N 维数组

输入信号，指定为实数值或复数值向量、矩阵或 N 维数组。x 包含的值必须为有限值。x 的长度必须大于滤波器阶数的三倍，定义为 max(length(B)-1, length(A)-1)。除非 x 是行向量，否则该函数沿 x 的第一个数组维度进行运算。如果 x 是行向量，则该函数沿第二个维度进行运算。

示例: cos(pi/4*(0:159))+randn(1,160) 是单通道行向量信号。

示例: cos(pi./[4;2]*(0:159))'+randn(160,2) 是双通道信号。

数据类型: double | single
复数支持: 是

`sos` — 二阶节系数
矩阵

二阶节系数，指定为矩阵。sos 是一个 L×6 矩阵，其中节数 L 必须大于或等于 2。如果节数小于 2，则该函数将输入视为分子向量。sos 的每行对应于二阶 (biquad) 滤波器的系数。sos 的第 i 行对应于 [bi(1) bi(2) bi(3) ai(1) ai(2) ai(3)]。

示例: s = [2 4 2 6 0 2;3 3 0 6 0 0] 用于指定一个归一化 3 dB 频率为 0.5π 弧度/采样点的三阶巴特沃斯滤波器。

数据类型: double | single

`g` — 尺度值
标量 | 向量

自 R2024b 起

尺度值，指定为具有 L + 1 个元素的实数值标量或实数值向量，其中 L 是 CTF 节的数量。尺度值表示滤波器增益在级联滤波器表示的各节之间的分布。

filtfilt 函数使用 scaleFilterSections 函数将增益应用于滤波器节，具体取决于您如何指定 g：

标量 - 函数将增益均匀分布在所有滤波器节上。
向量 - 函数将前 L 个增益值应用于对应的滤波器节，并将最后一个增益值均匀分布在所有滤波器节上。

数据类型: double | single

`d` — 数字滤波器
`digitalFilter` 对象

数字滤波器，指定为 digitalFilter 对象。使用 designfilt 根据频率响应设定生成数字滤波器。

示例: d = designfilt("lowpassiir",FilterOrder=3,HalfPowerFrequency=0.5) 用于指定一个归一化 3 dB 频率为 0.5π 弧度/采样点的三阶巴特沃斯滤波器。

`B,A` — 级联传递函数 (CTF) 系数
标量 | 向量 | 矩阵

自 R2024b 起

级联传递函数 (CTF) 系数，指定为标量、向量或矩阵。B 和 A 分别列出级联传递函数的分子系数和分母系数。

B 的大小必须为 L×(m + 1)，A 的大小必须为 L×(n + 1)，其中：

L 表示滤波器节的数量。
m 表示滤波器分子的阶。
n 表示滤波器分母的阶。

有关级联传递函数格式和系数矩阵的详细信息，请参阅以 CTF 格式指定数字滤波器。

注意

如果 A(:,1) 的任一元素不等于 1，则 filtfilt 按 A(:,1) 对滤波器系数进行归一化。在这种情况下，A(:,1) 必须为非零。

数据类型: double | single
复数支持: 是

输出参量

全部折叠

`y` — 滤波后的信号
向量 | 矩阵 | N 维数组

滤波后的信号，以向量、矩阵或 N 维数组形式返回。

filtfilt 函数返回与 x 大小相同的 y。
如果将任一输入参量指定为 single 类型，则 filtfilt 使用单精度算术计算滤波运算，并以 single 类型返回 y。否则，filtfilt 以 double 类型返回 y。

详细信息

全部折叠

级联传递函数

将 IIR 数字滤波器划分为级联节可提高其数值稳定性，并降低其对系数量化误差的易感性。以 L 传递函数 H₁(z)、H₂(z)、…、H_L(z) 表示的传递函数 H(z) 的级联形式为

$H (z) = \prod_{l = 1}^{L} H_{l} (z) = H_{1} (z) \times H_{2} (z) \times \dots \times H_{L} (z) .$

以 CTF 格式指定数字滤波器

您可以以 CTF 格式指定数字滤波器，用于分析、可视化和信号滤波。通过列出其系数 B 和 A 来指定滤波器。您还可以通过指定标量或向量 g 来包括各节的滤波器缩放增益。

滤波器系数

如果您将系数指定为 L 行矩阵

$B = [\begin{matrix} b_{11} & b_{12} & \dots & b_{1, m + 1} \\ b_{21} & b_{22} & \dots & b_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{L 1} & b_{L 2} & \dots & b_{L, m + 1} \end{matrix}], A = [\begin{matrix} a_{11} & a_{12} & \dots & a_{1, n + 1} \\ a_{21} & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{L 1} & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}],$

则假设您已将滤波器指定为一系列 L 级联传递函数，使得滤波器的完整传递函数为

$H (z) = \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{a_{11} + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{a_{21} + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{a_{L 1} + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}},$

其中 m ≥ 0 是滤波器的分子阶数，n ≥ 0 是分母阶数。

如果将 B 和 A 都指定为向量，则假设底层系统是一个单节 IIR 滤波器 (L = 1)，其中 B 表示传递函数的分子，A 表示其分母。
如果 B 是标量，则假设滤波器是所有极点 IIR 滤波器的级联，每个节的整体系统增益等于 B。
如果 A 是标量，则假设滤波器是 FIR 滤波器的级联，每个节的整体系统增益等于 1/A。

注意

要将二阶节矩阵转换为级联传递函数，请使用 sos2ctf 函数。
要将零极点增益滤波器表示转换为级联传递函数，请使用 zp2ctf 函数。

系数和增益

如果您有整体缩放增益或从系数值中析出的多个缩放增益，则可以将系数和增益指定为 {B,A,g} 形式的元胞数组。当您使用定点算术来确保每个滤波器节的输出具有相似的振幅水平时，定标滤波器节尤其重要，这有助于避免由于数值精度有限而导致滤波器响应不准确。

增益可以是标量整体增益或节增益向量。

如果增益是标量，则该值均匀地应用于所有级联滤波器节。
如果增益是向量，则它必须比级联中的滤波器节数 L 多一个元素。前 L 个尺度值中的每个值都应用于对应的滤波器节，最后一个值均匀地应用于所有级联滤波器节。

如果将系数矩阵和增益向量指定为

，则假设滤波器系统的传递函数为

$H (z) = g_{S} (g_{1} \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{a_{11} + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times g_{2} \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{a_{21} + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times g_{L} \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{a_{L 1} + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}}) .$

提示

您可以获得 CTF 格式的滤波器，包括缩放增益。使用数字 IIR 滤波器设计函数的输出，例如 butter、cheby1、cheby2 和 ellip。在这些函数中指定 "ctf" 滤波器类型参量，并指定返回 B、A 和 g 以获取尺度值。 (自 R2024b 起)

参考

[1] Gustafsson, F. “Determining the initial states in forward-backward filtering.” IEEE^® Transactions on Signal Processing. Vol. 44, April 1996, pp. 988–992. https://doi.org/10.1109/78.492552.

[2] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

[3] Mitra, Sanjit K. Digital Signal Processing. 2nd Ed. New York: McGraw-Hill, 2001.

[4] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

代码生成不支持 digitalFilter 对象。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

用法说明和限制：

代码生成不支持 digitalFilter 对象。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

此函数完全支持 GPU 数组。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2024b: 使用级联传递函数对信号进行滤波

filtfilt 函数支持级联传递函数 (CTF) 格式的输入。

另请参阅

filtfilt

语法

说明

示例

心电图波形的零相位滤波

线性啁啾的零相位级联滤波

从振荡信号中滤除正弦波伪影

输入参数

b, a — 传递函数系数 向量

x — 输入信号 向量 | 矩阵 | N 维数组

sos — 二阶节系数 矩阵

g — 尺度值 标量 | 向量

d — 数字滤波器 digitalFilter 对象

B,A — 级联传递函数 (CTF) 系数 标量 | 向量 | 矩阵

输出参量

y — 滤波后的信号 向量 | 矩阵 | N 维数组

详细信息

级联传递函数

以 CTF 格式指定数字滤波器

提示

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

版本历史记录

R2024b: 使用级联传递函数对信号进行滤波

另请参阅

主题

`b`, `a` — 传递函数系数
向量

`x` — 输入信号
向量 | 矩阵 | N 维数组

`sos` — 二阶节系数
矩阵

`g` — 尺度值
标量 | 向量

`d` — 数字滤波器
`digitalFilter` 对象

`B,A` — 级联传递函数 (CTF) 系数
标量 | 向量 | 矩阵

`y` — 滤波后的信号
向量 | 矩阵 | N 维数组

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。