旋转机械的振动分析

此示例说明如何使用时间同步平均法和包络频谱分析变速箱的振动信号。这些功能在变速箱的预测性维护中特别有用，变速箱包含多个旋转部件：齿轮、轴和轴承。

此示例生成并分析轴以固定速度旋转的变速箱的振动数据。使用时间同步平均法分离出与特定轴或齿轮相关联的振动分量，并平均掉所有其他分量。包络频谱在识别导致高频冲击的局部轴承故障时特别有用。

假设存在一个理想化的变速箱，它由一个 13 齿小齿轮和一个 35 齿大齿轮啮合组成。小齿轮与连接到原动机的输入轴耦合。大齿轮连接到输出轴。轴由变速箱外壳上的滚柱轴承支撑。两个加速度计 $A_{1}$ 和 $A_{2}$ 分别放置在轴承和变速箱外壳上。加速度计以 20 kHz 的采样率工作。

小齿轮以 $f_{Pinion}$ = 22.5 Hz 或 1350 rpm 速度旋转。齿轮和输出轴的转速为

$f_{Gear} = f_{Pinion} \times \frac{Number of pinion teeth (N_{p})}{Number of gear teeth (N_{g})}$ .

齿啮合频率，也称为齿轮啮合频率，是大齿轮和小齿轮的齿周期性啮合的速率：

$f_{Mesh} = f_{Pinion} \times N_{p} = f_{Gear} \times N_{g}$ .

rng default
fs = 20e3;          % Sample Rate (Hz)
Np = 13;            % Number of teeth on pinion
Ng = 35;            % Number of teeth on gear

fPin = 22.5;        % Pinion (Input) shaft frequency (Hz)
fGear = fPin*Np/Ng; % Gear (Output) shaft frequency (Hz)
fMesh = fPin*Np;    % Gear Mesh frequency (Hz)

为小齿轮和大齿轮生成振动波形。将振动建模为在主轴齿轮啮合频率下出现的正弦波。分析 20 秒的振动数据。

齿轮啮合波形负责传递负载，因此具有最高的振动振幅。 $A_{2}$ 记录两个轴和齿轮啮合产生的振动。对于本试验，轴承滚动元素对 $A_{2}$ 记录的振动信号的贡献可以忽略不计。可视化一段无噪声振动信号。

t = 0:1/fs:20-1/fs;

afIn = 0.4*sin(2*pi*fPin*t);     % Pinion waveform     
afOut = 0.2*sin(2*pi*fGear*t);   % Gear waveform

aMesh = sin(2*pi*fMesh*t);       % Gear-mesh waveform

aHealthy = afIn + afOut + aMesh; % Healthy gear signal

plot(t, afIn+afOut+aMesh)
xlim([0 0.25])
title("Noise-Free Signal for Healthy Gear")
xlabel("Time (s)")
ylabel("Acceleration (m/s^2)")
grid on

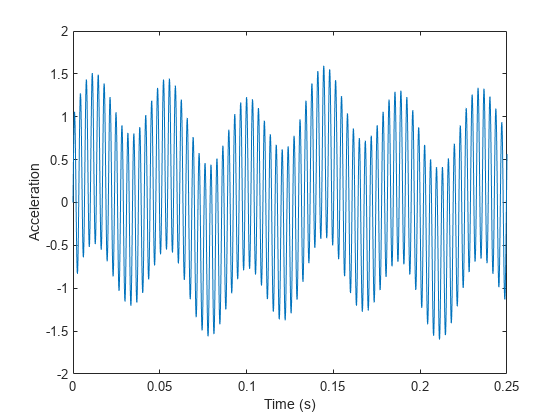
Figure contains an axes object. The axes object with title Noise-Free Signal for Healthy Gear, xlabel Time (s), ylabel Acceleration (m/s Squared baseline ) contains an object of type line.

生成由大齿轮齿上的局部故障引起的高频冲击

假设大齿轮的一个齿出现局部故障，如剥落。这导致大齿轮每旋转一周就会产生一次高频冲击。

局部故障造成的冲击持续时间短于齿啮合持续时间。大齿轮齿面上的凹痕会在冲击持续期间生成高频振荡。冲击频率取决于变速箱部件的特征及其固有频率。在此示例中，任意假设冲击产生 2 kHz 振动信号，持续时间约为 1/fMesh 的 8%，即 0.25 毫秒。大齿轮每转一圈，冲击就重复一次。

ipf = fGear;
fImpact = 2000;         

tImpact = 0:1/fs:2.5e-4-1/fs; 
xImpact = sin(2*pi*fImpact*tImpact)/3;

将冲击建模为一系列周期性脉冲，使其具有周期性。

xImpactPer = 2*pulstran(t,0:1/ipf:t(end),xImpact,fs);

将故障信号 xImpactPer 添加到轴信号中。将高斯白噪声添加到无故障和有故障大齿轮的输出信号，以对 $A_{2}$ 的输出建模。

aFaulty = aHealthy + xImpactPer;                              

aHealthyNoisy = aHealthy + randn(size(t))/5;
aFaultyNoisy = aFaulty + randn(size(t))/5;

可视化时间历史记录的一段。冲击位置在有故障大齿轮的图上用红色倒三角形表示。它们几乎无法辨识。

figure
tiledlayout flow

nexttile
plot(t,aHealthyNoisy)
title("Noisy Signal for Healthy Gear")
xlabel("Time (s)")
ylabel("Acceleration (m/s^2)")
axis([0.0 0.3 -2.5 2.5])

nexttile
plot(t,aFaultyNoisy)
hold on
Ind = (0.25*fs/fMesh):(fs/ipf):length(t);
Ind = round(Ind);
MarkX = t(Ind(1:3));
MarkY = 2.5;
scatter(MarkX,MarkY,"v","filled", ...
    MarkerFaceColor="#D95319")
hold off
title("Noisy Signal for Faulty Gear")
xlabel("Time (s)")
ylabel("Acceleration (m/s^2)")
axis([0.0 0.3 -2.5 2.5])

Figure contains 2 axes objects. Axes object 1 with title Noisy Signal for Healthy Gear, xlabel Time (s), ylabel Acceleration (m/s^2) contains an object of type line. Axes object 2 with title Noisy Signal for Faulty Gear, xlabel Time (s), ylabel Acceleration (m/s^2) contains 4 objects of type line, scatter.

比较两个信号的功率谱

局部齿故障导致分布边带出现在齿轮啮合频率附近：

$f_{s ide b and, Pinion} = f_{Mesh} \pm m \times f_{Pinion} \forall m \in {1, 2, 3, . .}$

$f_{s ide b and, Gear} = f_{Mesh} \pm m \times f_{Gear} \forall m \in {1, 2, 3, . .}$

计算正常齿轮和故障齿轮的频谱。指定频率范围，包括 8.35 Hz 和 22.5 Hz 的轴频率以及 292.5 Hz 的齿轮啮合频率。

[Spect,f] = pspectrum([aHealthyNoisy' aFaultyNoisy'], ...
    fs,FrequencyResolution=0.2,FrequencyLimits=[0 500]);

绘制频谱图。由于故障在大齿轮上而不是在小齿轮上，因此边带预计出现在频谱上的 $f_{s ide b and, Gear}$ 处，间隔为 $f_{Gear}$ 。频谱显示了 fGear、fPin 和 fMesh 处的预期峰值。然而，信号中噪声的存在使得无法辨识 $f_{s ide b and, Gear}$ 处的边带峰值。

figure
plot(f,pow2db(Spect(:,1)), ...
     f,pow2db(Spect(:,2)),"-.")
hold on
scatter([fGear fPin fMesh],0,"v","filled")
hold off
xlabel("Frequency (Hz)")
ylabel("Power Spectrum (dB)")
legend("Healthy Gear","Faulty Gear","f_{Gear}","f_{Pinion}","f_{Mesh}")
grid on

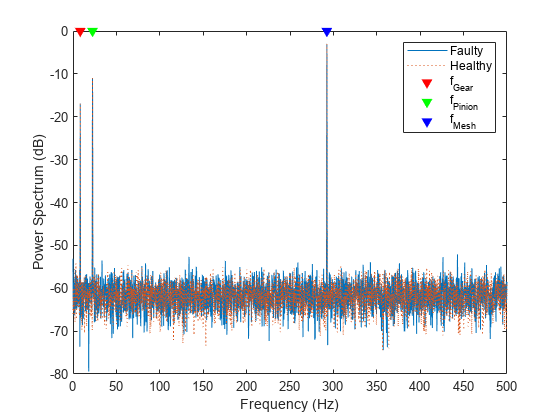
$Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 5 objects of type line, scatter. These objects represent Healthy Gear, Faulty Gear, f_{Gear}, f_{Pinion}, f_{Mesh}.$

放大齿轮啮合频率的附近区域。创建在 $f_{s ide b and, Gear}$ 和 $f_{s ide b and, Pinion}$ 处大齿轮和小齿轮边带的网格。

figure
p1 = plot(f,pow2db(Spect(:,1)));
hold on
p2 = plot(f,pow2db(Spect(:,2)),"-.");

harmonics = -5:5;
SBandsGear = (fMesh+fGear.*harmonics);
SBandsPinion = (fMesh+fPin.*harmonics);
p3 = xline(SBandsGear,"-.",Color="#EDB120");
p4 = xline(SBandsPinion,"--");
hold off

axis([250 340 -70 -40])
xlabel("Frequency (Hz)")
ylabel("Power Spectrum (dB)")
legend([p1 p2 p3(1) p4(1)], ...
    ["Healthy Gear";"Faulty Gear"; ...
    "f_{sideband,Gear}";"f_{sideband,Pinion}"])

$Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 24 objects of type line, constantline. These objects represent Healthy Gear, Faulty Gear, f_{sideband,Gear}, f_{sideband,Pinion}.$

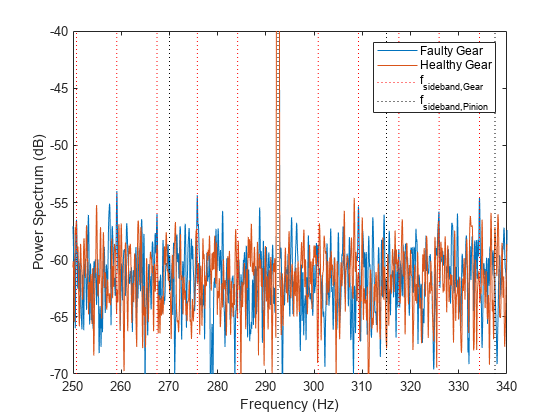
目前尚不清楚峰值是否与大齿轮边带 $f_{s ide b and, Gear}$ 对齐。

对输出振动信号应用时间同步平均法

请注意，很难区分在大齿轮边带 $f_{SideBand, Gear}$ 和小齿轮边带 $f_{SideBand, Pinion}$ 上的峰值。由上一节可知，区分峰值和确定小齿轮或大齿轮是否受故障影响十分困难。时间同步平均法会平均掉零均值随机噪声和与特定轴频率无关联的任何波形。这使得故障检测过程更加容易。

使用函数 tsa 为小齿轮和大齿轮生成时间同步波形。

为小齿轮指定时间同步脉冲。计算小齿轮 10 转的时间同步平均值。

tPulseIn = 0:1/fPin:max(t);
taPin = tsa(aFaultyNoisy,fs,tPulseIn,NumRotations=10);

指定大齿轮的时间同步脉冲。计算大齿轮 10 转的时间同步平均值。

tPulseOut = 0:1/fGear:max(t);
taGear = tsa(aFaultyNoisy,fs,tPulseOut,NumRotations=10);

可视化 1 转的时间同步信号。在大齿轮的时间同步平均化后的信号上，这种冲击相对更容易看到，而这种冲击在小齿轮轴上因平均化而不易辨识。图上用标记指示的冲击位置比相邻的齿轮啮合峰值具有更高的振幅。

不带输出参量的 tsa 函数绘制时间同步平均信号和对应于当前图窗中每个信号段的时域信号。

figure
tiledlayout flow

nexttile
tsa(aFaultyNoisy,fs,tPulseIn,NumRotations=10)
axis([0.5 1.5 -2 2])
title("TSA Signal for Pinion")

nexttile
tsa(aFaultyNoisy,fs,tPulseOut,NumRotations=10)
hold on
scatter(1.006,2,"v","filled")
hold off
axis([0.5 1.5 -2 2])
title("TSA Signal for Gear")

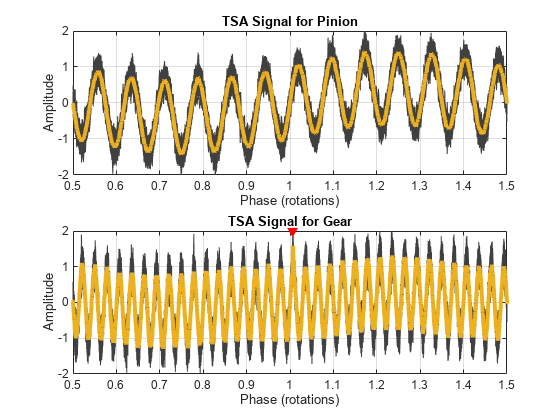
Figure contains 2 axes objects. Axes object 1 with title TSA Signal for Pinion, xlabel Phase (rotations), ylabel Amplitude contains 45 objects of type line. Axes object 2 with title TSA Signal for Gear, xlabel Phase (rotations), ylabel Amplitude contains 18 objects of type line, scatter.

可视化时间同步平均化后的信号的功率谱

计算时间同步平均化后的齿轮信号的功率谱。在齿轮啮合频率 292.5 Hz 的任一侧，指定一个涵盖 15 个齿轮边带的频率范围。请注意 $f_{s ide b and, Gear}$ 处的峰值。

figure
pspectrum(taGear,fs, ...
    FrequencyResolution=2.2,FrequencyLimits=[200 400])

harmonics = -15:15;
SBandsGear=(fMesh+fGear.*harmonics);
xline(fMesh,"--",Color="#D95319")
xline(SBandsGear,":")

grid off
title("TSA Gear (Output Shaft)")
legend("Power Spectrum","Gear-Mesh Frequency","f_{sideband,Gear}")

$Figure contains an axes object. The axes object with title TSA Gear (Output Shaft), xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 33 objects of type line, constantline. These objects represent Power Spectrum, Gear-Mesh Frequency, f_{sideband,Gear}.$

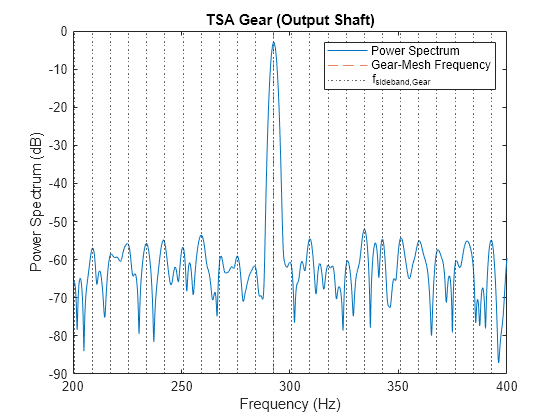
将相同频率范围内的小齿轮信号时间同步平均化并可视化其功率谱。这次，在 $f_{s ide b and, Pinion}$ 频率位置绘制网格线。

figure
pspectrum(taPin,fs, ...
    FrequencyResolution=5.8,FrequencyLimits=[200 400])

SBandsPinion = (fMesh+fPin.*harmonics);
xline(fMesh,"--",Color="#D95319")
xline(SBandsPinion,":")

grid off
title("TSA Pinion (Input Shaft)")
legend("Power Spectrum","Gear-Mesh Frequency","f_{sideband,Pinion}")

$Figure contains an axes object. The axes object with title TSA Pinion (Input Shaft), xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 33 objects of type line, constantline. These objects represent Power Spectrum, Gear-Mesh Frequency, f_{sideband,Pinion}.$

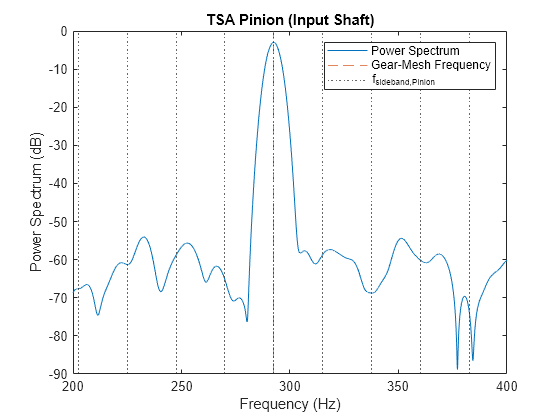
请注意图中 $f_{s ide b and, Pinion}$ 处没有明显的峰值。

原始信号的功率谱包含来自两个不同轴的波形以及噪声。很难辨识边带谐波。然而，我们可以观察到时间同步平均化后的大齿轮信号频谱边带位置的显著峰值。还可以观察到边带幅值具有非均匀性，这表示存在齿轮局部故障。另一方面，时间同步平均化后的小齿轮信号的频谱中没有边带峰值。这有助于我们得出小齿轮工作正常的结论。

tsa 函数通过对不相关波形平均化使其不易辨识和观察边带谐波来帮助识别故障齿轮。当希望从具有多个轴和齿轮的变速箱中提取对应于单个轴的振动信号时，此功能尤其有用。

在小齿轮中添加一个分布式故障，并将其影响纳入振动信号

分布式齿轮故障，如偏心或齿轮错位 [1]，会导致较高水平的边带，这些边带在齿轮啮合频率的整数倍附近紧密分组。

为了对分布式故障进行仿真，我们在齿轮啮合频率的两侧引入振幅递减的三个边带分量。

SideBands = -3:3;
SideBandAmp = [0.02 0.1 0.4 0 0.4 0.1 0.02]; % Sideband amplitudes
SideBandFreq = fMesh + SideBands*fPin;       % Sideband frequencies

vSideBands = SideBandAmp*sin(2*pi*SideBandFreq'.*t);

将边带信号添加到振动信号中。这会导致振幅调制。

vPinFaultNoisy = aFaultyNoisy + vSideBands;

可视化受分布式故障影响的变速箱的一段时间历史记录。

plot(t,vPinFaultNoisy)
xlim([0.6 0.85])
title("Effects of Sideband Modulation")
xlabel("Time (s)")
ylabel("Acceleration (m/s^2)")

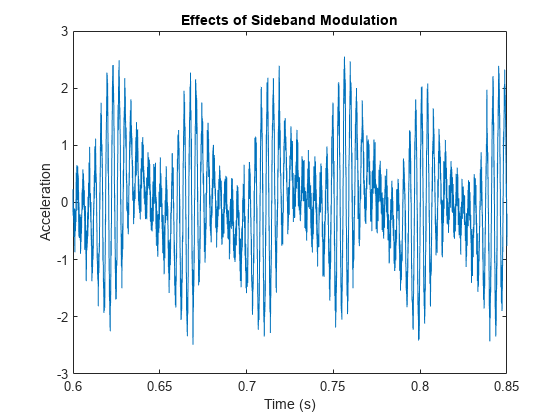
Figure contains an axes object. The axes object with title Effects of Sideband Modulation, xlabel Time (s), ylabel Acceleration (m/s Squared baseline ) contains an object of type line.

重新计算小齿轮和大齿轮的时间同步平均化后的信号。

taPin = tsa(vPinFaultNoisy,fs,tPulseIn,NumRotations=10);
taGear = tsa(aFaultyNoisy,fs,tPulseOut,NumRotations=10);

可视化时间同步平均化后的信号的功率谱。小齿轮的时间同步平均化后的信号中的三条边带更明显，这表明存在分布式故障。但是，时间同步平均化后的齿轮信号的频谱保持不变。

figure
tiledlayout flow

nexttile
pspectrum(taPin,fs, ...
    FrequencyResolution=5.8,FrequencyLimits=[200 400])
xline(SBandsPinion,":")
grid off
title ("TSA Pinion (Input Shaft)")
legend("Power Spectrum","f_{sideband,Pinion}")

nexttile
pspectrum(taGear,fs, ...
    FrequencyResolution=2.2,FrequencyLimits=[200 400])
xline(SBandsGear,":")
grid off
title ("TSA Gear (Output Shaft)")
legend("Power Spectrum","f_{sideband,Gear}")

$Figure contains 2 axes objects. Axes object 1 with title TSA Pinion (Input Shaft), xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 32 objects of type line, constantline. These objects represent Power Spectrum, f_{sideband,Pinion}. Axes object 2 with title TSA Gear (Output Shaft), xlabel Frequency (Hz), ylabel Power Spectrum (dB) contains 32 objects of type line, constantline. These objects represent Power Spectrum, f_{sideband,Gear}.$

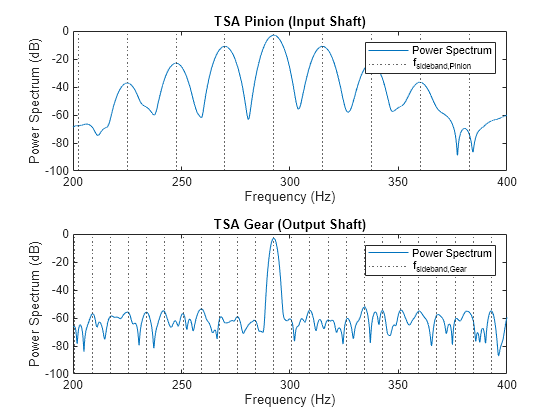
总的来说，tsa 函数有助于从整体振动信号中提取大齿轮和小齿轮对应的振动信号。这反过来有助于识别受局部故障和分布式故障影响的特定部件。

滚动元素轴承故障的振动分析

滚动元素轴承的局部故障可能发生在外圈、内圈、保持架或滚动元素中。其中每个故障都由自己的频率表征，该频率通常由制造商列出或根据轴承设定计算。局部故障的冲击会在轴承和响应传导器之间的变速箱结构中生成高频振动 [2]。假设变速箱中的齿轮状况良好，并且支撑小齿轮轴的轴承之一受到内圈局部故障的影响。在分析中忽略径向负载的影响。

轴承的节径为 12 厘米，有八个滚动元素。每个滚动元素的直径为 2 厘米。接触角 $θ$ 为 $15^{\circ}$ 。在分析轴承振动时，通常将加速度计放在轴承外壳上。加速度测量值由位于故障轴承外壳上的加速度计 $A_{1}$ 记录。

定义轴承的参数。

n = 8;         % Number of rolling element bearings
d = 0.02;      % Diameter of rolling elements 
p = 0.12;      % Pitch diameter of bearing
thetaDeg = 15; % Contact angle in degrees

每当滚动元素经过内圈的局部故障时，就会发生冲击。冲突发生速率即球经过内圈的频率 (BPFI)。BPFI 可以通过以下方式计算

$f_{BPFI} = \frac{n {\times f}_{Pin}}{2} (1 + \frac{d}{p} \cos θ)$ .

bpfi = n*fPin/2*(1 + d/p*cosd(thetaDeg))

bpfi = 
104.4889

将每次冲击建模为 3 kHz 正弦波，用凯塞窗进行加窗。该缺陷会对轴承造成一系列 5 毫秒的冲击。凹坑和散裂早期阶段的冲激频率范围很宽，最高可达 100 kHz [2]。将冲击建模为用凯塞窗进行加窗的一系列 3 kHz 周期性正弦波。由于 $A_{1}$ 更靠近轴承，请调整冲击的振幅，使其相对于 $A_{2}$ 记录的变速箱振动信号更突出。

fImpact = 3000;
tImpact = 0:1/fs:5e-3-1/fs;
xImpact = sin(2*pi*fImpact*tImpact) ...
    .*kaiser(length(tImpact),40)';

xImpactBper = 0.33*pulstran(t,0:1/bpfi:t(end),xImpact,fs);

可视化冲击信号。

figure
plot(t,xImpactBper)
xlim([0 0.05])
title(["Impacts Due to Local Fault" ...
    "on the Inner Race of the Bearing"])
xlabel("Time (s)")
ylabel("Acceleration (m/s^2)")

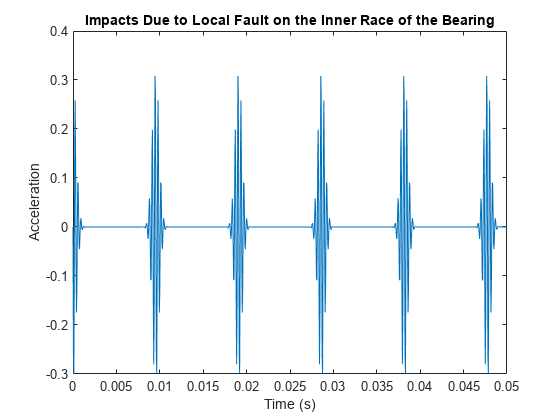
Figure contains an axes object. The axes object with title Impacts Due to Local Fault on the Inner Race of the Bearing, xlabel Time (s), ylabel Acceleration (m/s Squared baseline ) contains an object of type line.

将周期性轴承故障添加到来自正常变速箱的振动信号中。

vNoBFaultNoisy = aHealthy + randn(size(t))/5;
vBFaultNoisy = xImpactBper + aHealthy + randn(size(t))/5;

计算信号的频谱。可视化较低频率的频谱。创建一个包含前十个 BPFI 谐波的网格。

pspectrum([vBFaultNoisy' vNoBFaultNoisy'],fs, ...
    FrequencyResolution=1,FrequencyLimits=[0 10*bpfi])
grid off

harmImpact = (0:10)*bpfi;
xline(harmImpact/1000,":")
xlim([0 10*bpfi]/1000)
title("Bearing Vibration Spectra")
legend("Healthy","Damaged","BPFI harmonics")

Figure contains an axes object. The axes object with title Bearing Vibration Spectra, xlabel Frequency (kHz), ylabel Power Spectrum (dB) contains 13 objects of type line, constantline. These objects represent Healthy, Damaged, BPFI harmonics.

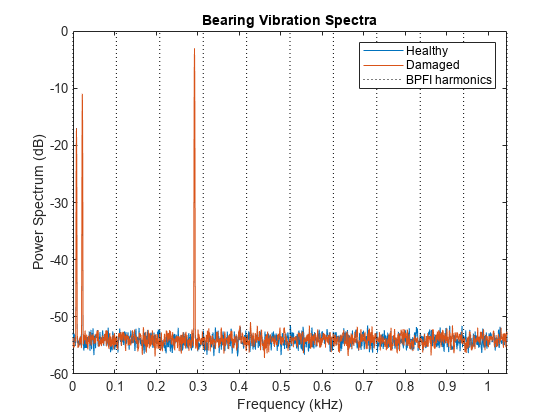
在频谱图的下端，轴和啮合频率的绘图及其顺序掩盖了其他特征。正常轴承的频谱和受损轴承的频谱无法区分。因此，必须采用一种能够隔离轴承故障的方法。

BPFI 取决于比率 $d / p$ 和接触角 $θ$ 的余弦值。BPFI 的无理数表达式表示轴承冲击次数与轴的整数转数不同步。tsa 函数在这种情况下不适用，因为它会对冲击进行平均化而使其无法辨识。冲击不在每个平均段的同一位置。

函数 envspectrum（包络频谱）执行振幅解调，可用于提取有关高频冲击的信息。

计算并绘制包络信号及其频谱。将有故障和无故障的轴承信号的包络频谱进行比较。可视化较低频率的频谱。创建一个包含前十个 BPFI 谐波的网格。

figure
envspectrum([vNoBFaultNoisy' vBFaultNoisy'],fs)

xline(harmImpact/1000,":")
xlim([0 10*bpfi]/1000)
legend("Healthy","Damaged","BPFI harmonics")

Figure contains 2 axes objects. Axes object 1 with title Envelope Signal, xlabel Time (secs), ylabel Amplitude contains 2 objects of type line. Axes object 2 with title Envelope Spectrum, xlabel Frequency (kHz), ylabel Peak Amplitude contains 13 objects of type line, constantline. These objects represent Healthy, Damaged, BPFI harmonics.

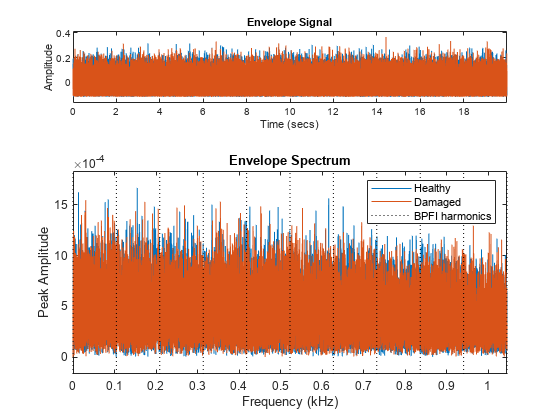
请注意 BPFI 峰值在包络频谱中不突出，因为噪声污染了信号。回想一下，执行 tsa 来平均化噪声对于轴承故障分析不适用，因为它也会平均化冲击信号。

envspectrum 函数提供一个内置滤波器，可用于去除感兴趣的频带以外的噪声。应用一个中心频率为 3.125 kHz、宽度为 4.167 kHz 的 200 阶带通滤波器。

Fc = 3125;
BW = 4167;

envspectrum([vNoBFaultNoisy' vBFaultNoisy'],fs, ...
    Method="hilbert",FilterOrder=200,Band=[Fc-BW/2 Fc+BW/2])   

harmImpact = (0:10)*bpfi;
xline(harmImpact/1000,":")
xlim([0 10*bpfi]/1000)
legend("Healthy","Damaged","BPFI harmonics")

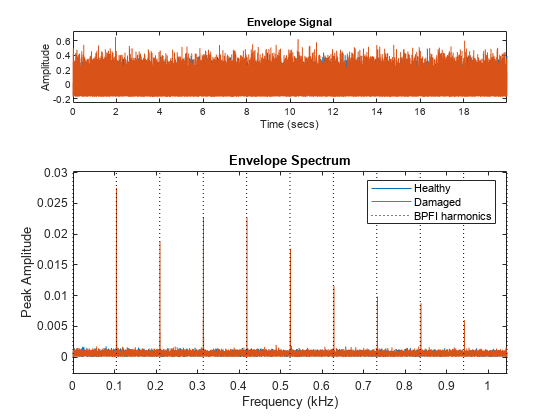
包络频谱有效地将通带内容带入基带，因此在低于 1 kHz 的 BPFI 谐波处显示出明显的峰值。这有助于得出轴承内圈可能损坏的结论。

在本例中，故障轴承的频谱清楚地显示由冲击频率调制的 BPFI 谐波。在频谱中可视化这种现象，接近 3 kHz 冲击频率。

figure 
pspectrum([vNoBFaultNoisy' vBFaultNoisy'],fs, ...
    FrequencyResolution=1, ...
    FrequencyLimits=(bpfi*[-10 10]+fImpact))
grid off
legend("Healthy","Damaged")
title("Bearing Vibration Spectra")

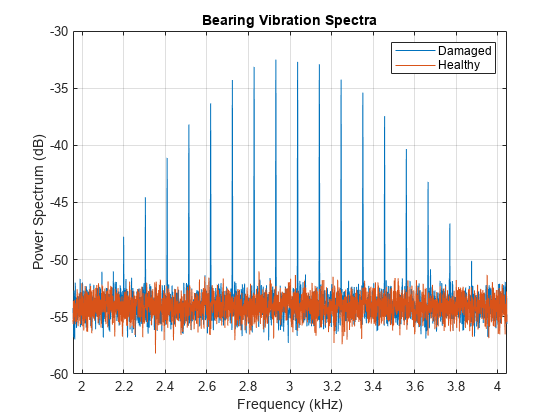
Figure contains an axes object. The axes object with title Bearing Vibration Spectra, xlabel Frequency (kHz), ylabel Power Spectrum (dB) contains 2 objects of type line. These objects represent Healthy, Damaged.

观察到峰值之间的频率分离等于 BPFI。

结论

此示例使用时间同步平均法来分离与小齿轮和大齿轮相关联的振动信号。此外，tsa 还能够衰减随机噪声。在速度波动（和存在负载 [2]）的情况下，可先使用阶跟踪来根据轴旋转角度对信号进行重采样，再使用 tsa。时间同步平均法也用于试验条件，以衰减轴速度微小变化的影响。

轴承故障分析宜从宽带频率分析开始 [3]。然而，当轴承冲击频率附近的频谱包含来自其他分量的贡献时，例如变速箱中齿轮啮合频率的高次谐波，则轴承故障分析不一定很有用。在这种情况下，包络分析很有用。函数 envspectrum 可用于提取故障轴承的包络信号和频谱，作为轴承磨损和损坏的指标。

参考资料

Scheffer, Cornelius, and Paresh Girdhar.Practical Machinery Vibration Analysis and Predictive Maintenance.Amsterdam:Elsevier, 2004.
Randall, Robert Bond.Vibration Based Condition Monitoring:Industrial, Aerospace and Automotive Applications.Chichester, UK:John Wiley and Sons, 2011.
Lacey, S. J. An Overview of Bearing Vibration Analysis.（来源：http://www.maintenanceonline.co.uk/maintenanceonline/content_images/p32-42%20Lacey%20paper%20M&AM.pdf）
Brandt, Anders.Noise and Vibration Analysis:Signal Analysis and Experimental Procedures.Chichester, UK:John Wiley and Sons, 2011.

另请参阅

envspectrum | pspectrum | tsa

主题

Machine Learning and Deep Learning Classification Using Signal Feature Extraction Objects