Machine Learning and Deep Learning Classification Using Signal Feature Extraction Objects

Introduction

Rotating machines that use bearings are widely employed in various industrial applications, such as medical devices, food processing, semiconductors, paper making, and aircraft components. These industrial systems often suffer from electric current discharged through the bearings that can result in motor bearing failure within a few months of system startup. Failure to detect these issues in a timely manner can cause significant downtime in system operations. In addition to requiring regularly scheduled maintenance, the industrial system using rotating machines needs continuous monitoring for bearing current detection to ensure safety, reliability, efficiency, and performance.

Significant research work has been dedicated to automatic identification of faulty bearings in industrial systems. Reliable, effective, and efficient feature extraction techniques play a key role in AI-based fault diagnosis performance [1], [2]. As the bearing current is caused by variable speed conditions, the fault frequencies can sweep up or down in the frequency range over time as the speed varies. In other words, bearing vibration signals are nonstationary in nature. The nonstationary characteristics can be captured well by various time-frequency representations. Combined features extracted from the time, frequency, and time-frequency representations of the signals can be used to improve the fault detection performance of systems [3].

Download and Prepare the Data

The data set contains acceleration signals collected from rotating machines in bearing test rig and real-world machines such as oil pump bearings, intermediate speed bearings, and a planet bearing. There are 34 files in total. The signals in the files are sampled at fs = 25 Hz. The filenames describe the signals they contain:

Download the data files into your temporary directory, whose location is specified by the tempdir command in MATLAB®. If you want to place the data files in a folder different from tempdir, change the directory name in the subsequent instructions. Create a signalDatastore object to access the data in the files and obtain the labels.

dataURL = 'https://www.mathworks.com/supportfiles/SPT/data/rollingBearingDataset.zip';
datasetFolder = fullfile(tempdir,'rollingBearingDataset');
zipFile = fullfile(tempdir,'rollingBearingDataset.zip');
if ~exist(datasetFolder,'dir')
    websave(zipFile,dataURL);
    unzip(zipFile,datasetFolder);
end

% Create a datastore using the support files
sds = signalDatastore(datasetFolder);

The dataset filenames contain the label names. Get a list of labels from the filenames in the datastore using the filenames2labels function.

labels = filenames2labels(sds,ExtractBefore='_');

% Shorten labels for better display
labels = getShortenedLabels(labels);

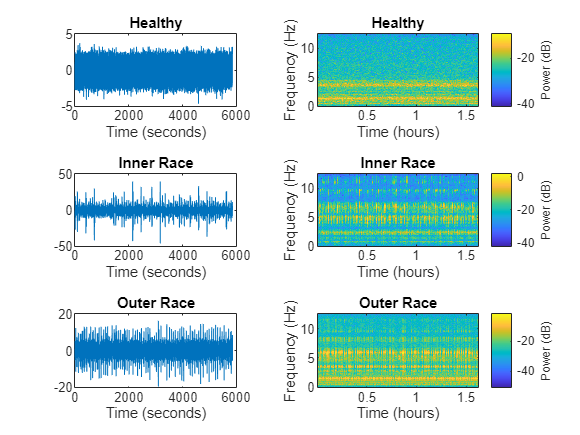
Analyze one instance of a healthy signal, one of a signal with inner race faults, and one of a signal with outer race faults. The spectrogram for the healthy signal shows that the frequency content over time is more concentrated in the low-frequency range. In contrast, the spectrograms for the faulty signals are spread out in both the low-frequency range and in the high-frequency range. Features extracted from spectrograms can capture these characteristics.

healthySignal = read(subset(sds,1));
innerRaceFaultSignal = read(subset(sds,13));
outerRaceFaultSignal = read(subset(sds,34));

fs = 25;

figure
tiledlayout(3,2)
nexttile
plot((0:numel(healthySignal)-1)/fs,healthySignal)
xlabel("Time (seconds)")
title("Healthy")
nexttile
pspectrum(healthySignal,fs,"spectrogram",Leakage=0.9)
title("Healthy")

nexttile
plot((0:numel(innerRaceFaultSignal)-1)/fs,innerRaceFaultSignal)
xlabel("Time (seconds)")
title("Inner Race")
nexttile
pspectrum(innerRaceFaultSignal,fs,"spectrogram",Leakage=0.9)
title("Inner Race")

nexttile
plot((0:numel(outerRaceFaultSignal)-1)/fs,outerRaceFaultSignal)
xlabel("Time (seconds)")
title("Outer Race")
nexttile
pspectrum(outerRaceFaultSignal,fs,"spectrogram",Leakage=0.9)
title("Outer Race")

Setup Feature Extraction Objects

In this section you setup feature extraction objects that extract multidomain features from the signals. These features will be used to implement machine learning and deep learning solutions to classify signals as healthy, as having inner race faults, or as having outer race faults.

Use the signalTimeFeatureExtractor, signalFrequencyFeatureExtractor, and signalTimeFrequencyFeatureExtractor objects to extract features from all the signals.

Create a time-domain feature extractor to extract time domain features.

timeFE = signalTimeFeatureExtractor(SampleRate=25, ...
    RMS=true, ...
    ImpulseFactor=true, ...
    StandardDeviation=true, ...
    ClearanceFactor=true);

Create a frequency-domain feature extractor to extract frequency domain features.

 freqFE = signalFrequencyFeatureExtractor(SampleRate=25, ...
    MedianFrequency=true, ...
    BandPower=true, ...
    PowerBandwidth=true, ...
    PeakAmplitude=true);

Create a time-frequency feature extractor to extract time-frequency features. To extract the time-frequency features, use a spectrogram with 90% leakage.

 timeFreqFE = signalTimeFrequencyFeatureExtractor(SampleRate=25, ...
    SpectralKurtosis=true, ...
    SpectralSkewness=true, ...
    SpectralFlatness=true, ...
    TFRidges=true, ...
    ScaleSpectrum=true);

setExtractorParameters(timeFreqFE,"spectrogram",Leakage=0.9);

Train an SVM Classifier Using Multidomain Features

Extract Multidomain Features

Extract features using all three features extractors for the signals in the signalDatastore.

Concatenate the extracted features to obtain a feature matrix. You can use the feature matrix and its corresponding labels to train a multiclass SVM classifier.

SVMFeatures = cellfun(@(a,b,c) [a b c],extract(timeFE,sds),...
    extract(freqFE,sds),extract(timeFreqFE,sds),UniformOutput=false);

featureMatrix = cell2mat(SVMFeatures);

Train an SVM Classifier Model

Obtain a feature table from the multidomain feature matrix that will be used to train a multiclass SVM classifier and observe the classification accuracy.

featureTable = array2table(featureMatrix);

head(featureTable(:,1:20))

    featureMatrix1    featureMatrix2    featureMatrix3    featureMatrix4    featureMatrix5    featureMatrix6    featureMatrix7    featureMatrix8    featureMatrix9    featureMatrix10    featureMatrix11    featureMatrix12    featureMatrix13    featureMatrix14    featureMatrix15    featureMatrix16    featureMatrix17    featureMatrix18    featureMatrix19    featureMatrix20
    ______________    ______________    ______________    ______________    ______________    ______________    ______________    ______________    ______________    _______________    _______________    _______________    _______________    _______________    _______________    _______________    _______________    _______________    _______________    _______________

       0.89042           0.87979            7.7551            6.5588            3.4342           0.79563          0.00031429          1.6299            3.1851            2.9578             2.7979             3.5073             3.3425             3.2894             3.0054             2.9904              3.615             3.4075             3.1688             2.8402     
       0.86631           0.86443            6.9682            5.9044            3.4533           0.74962          0.00032232           1.425            3.0094            2.9463             2.9195             2.7414             2.9711             3.2231             3.2464             3.0089             3.0951             2.7609             2.6541               3.34     
       0.87483           0.87293            7.2224            6.1184            3.4211           0.76698          0.00031299          2.2829            2.8604            2.8134             2.8711             3.1266             2.9899              2.894             2.6456             2.6727             2.9572             2.6347             2.6946             2.7945     
       0.89696           0.89521            6.5476            5.5462            3.3956           0.80326          0.00031824          2.1562            2.9741             3.028             2.9558             3.5788             3.2329             2.8973             2.8414             3.3408             3.6882             3.2481             2.9149             3.3298     
       0.88766           0.87685            7.2062            6.1101            3.4234           0.78838          0.00031655          1.5097            3.1028            3.0025             2.7755             3.1872             3.0653             3.0677             3.1056             2.7412             2.9906             2.9219             2.9751             3.0733     
       0.88632           0.87554            6.7042            5.6771             3.443           0.78578          0.00032104          1.5016            3.1885            2.9341              3.117             3.1114             3.1284             2.8476               3.21             2.7989             3.1023             2.7537              3.077             2.8268     
       0.89654           0.88599            6.8998            5.8484            3.4144            0.8064          0.00031895          1.7236            3.2226            3.3195              3.093             3.0102             3.0166             3.1309             3.2455              3.374             3.3268             3.2598             3.0828             3.1874     
       0.86256           0.85424            7.1177            6.0223            3.5046           0.74237          0.00030795          0.8972            2.8081            2.8225             2.7826             3.2795             3.6573             2.9128             2.6972              3.029             3.0403             3.1295             2.5442             3.3955     

Split the feature table into training and testing feature data sets. Obtain their corresponding labels. For reproducible results, reset the random seed generator.

rng default

cvp = cvpartition(labels,Holdout=0.25);

trainingPredictors = featureTable(cvp.training,:);
trainingResponse = labels(cvp.training,:);

testPredictors = featureTable(cvp.test,:);
testResponse = labels(cvp.test,:);

Use the training features to train a multiclass SVM classifier.

SVMModel = fitcecoc(trainingPredictors,trainingResponse);

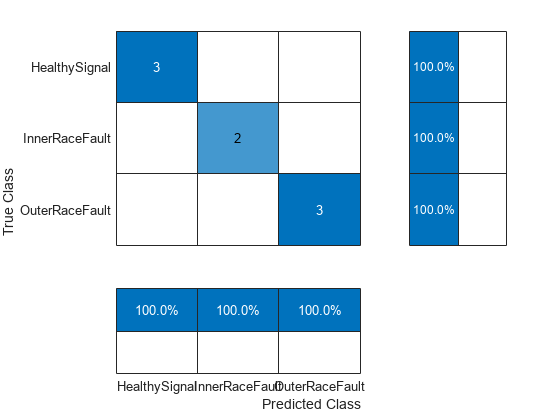
Use the test features to identify the faulty signals and analyze the accuracy of the classifier.

predictedLabels = predict(SVMModel,testPredictors);

figure
cm = confusionchart(testResponse,predictedLabels,...
    ColumnSummary="column-normalized",RowSummary="row-normalized");

Calculate the classifier accuracy.

accuracy = trace(cm.NormalizedValues)/sum(cm.NormalizedValues,"all");
fprintf("The classification accuracy on the test partition is %2.1f%%",accuracy*100)

The classification accuracy on the test partition is 100.0%

Train an LSTM Network Using Multidomain Features

Setup Feature Extraction Objects for Training an LSTM Network

Each signal in the signalDatastore object sds has around 150,000 samples. Window each signal into 1000-sample signal frames and extract multidomain features from it using all three feature extractors. You can achieve this by setting the FrameSize for all three feature extractors to 1000.

timeFE.FrameSize = 1000;
freqFE.FrameSize = 1000;
timeFreqFE.FrameSize = 1000;

Features extracted from frames correspond to a sequence of features over time that have lower dimension than the original signal. The dimension reduction helps the LSTM network to train faster. The workflow follows these steps:

Split the labels into training and testing sets. Use 70% of the labels for training set and the remaining 30% for testing data. Use splitlabels to obtain the desired partition of the labels. This guarantees that each split data set contains similar label proportions as the entire data set. Obtain the corresponding datastore subsets from the signalDatastore. Reset the random number generator for reproducible results.

rng default

splitIndices = splitlabels(labels,0.7,"randomized");
trainIdx = splitIndices{1};
countlabels(labels(splitIndices{1}))

ans=3×3 table
      Label      Count    Percent
    _________    _____    _______

    Healthy        8      33.333 
    InnerRace      5      20.833 
    OuterRace     11      45.833 

testIdx = splitIndices{2};
countlabels(labels(splitIndices{2}))

ans=3×3 table
      Label      Count    Percent
    _________    _____    _______

    Healthy        4        40   
    InnerRace      2        20   
    OuterRace      4        40   

trainDs = subset(sds,trainIdx);
trainLabels = labels(trainIdx);
testDs = subset(sds,testIdx);
testLabels = labels(testIdx);

For each 146484 sample long signal in the training signalDatastore, obtain a 146-by-127 multidomain feature matrix. The framing process reduces the number of samples to train the network by a factor of 7.9. If the signals are fed into the LSTM network directly (as shown in the figure), the network needs to learn the long-term dependencies among 146484 samples.

In contrast, after the framing and feature extraction process (as seen in the figure), the LSTM network needs to learn the long-term dependencies from a sequence of features over 146 time instances, a significantly lower number than the original time sequence length.

As a result, the LSTM network needs less complexity (less number of hidden units) and less time to train and perform successful classification.

Extract Multidomain Features

Obtain features from the training datastore using all three feature extractors.

trainFeatures = cellfun(@(a,b,c) [a b c],extract(timeFE,trainDs),...
    extract(freqFE,trainDs),extract(timeFreqFE,trainDs),UniformOutput=false);

Follow the same workflow to obtain test features.

testFeatures = cellfun(@(a,b,c) [a b c],extract(timeFE,testDs),...
    extract(freqFE,testDs),extract(timeFreqFE,testDs),UniformOutput=false);

Train an LSTM Network

Train the network using the training features and their corresponding labels.

numFeatures = size(trainFeatures{1},2);
numClasses = 3;

layers = [ ...
    sequenceInputLayer(numFeatures)
    lstmLayer(50,OutputMode="last")
    fullyConnectedLayer(numClasses)
    softmaxLayer];
 
options = trainingOptions("adam", ...
    Shuffle="every-epoch", ...    
    Plots="training-progress", ...
    ExecutionEnvironment="cpu", ...
    MaxEpochs=80, ...
    Verbose=false);

net = trainnet(trainFeatures,trainLabels,layers,"crossentropy",options);

Use the trained network to classify the signals in the test dataset and analyze the accuracy of the network.

scores = minibatchpredict(net,testFeatures);
classNames = categories(labels);
predTest = scores2label(scores,classNames);

figure
cm = confusionchart(testLabels,predTest, ...
     ColumnSummary="column-normalized",RowSummary="row-normalized");

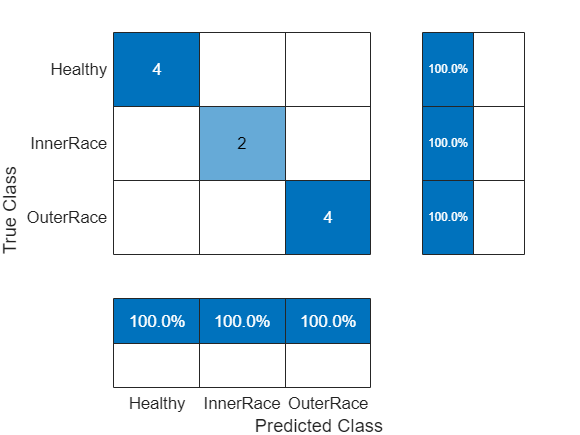
Calculate the classifier accuracy.

accuracy = trace(cm.NormalizedValues)/sum(cm.NormalizedValues,"all");
fprintf("The classification accuracy on the test partition is %2.1f%%",accuracy*100)

The classification accuracy on the test partition is 100.0%

Summary

This example uses multidomain signal feature extraction together with an SVM classifier and an LSTM deep learning network for motor bearing fault detection. To learn how to extract features and train models using a parallel pool of workers, see Accelerate Signal Feature Extraction and Classification Using a Parallel Pool of Workers. To learn how to extract features and train models using a GPU, see Accelerate Signal Feature Extraction and Classification Using a GPU.

References

[1] Cheng, Cheng, Guijun Ma, Yong Zhang, Mingyang Sun, Fei Teng, Han Ding, and Ye Yuan. “A Deep Learning-Based Remaining Useful Life Prediction Approach for Bearings.” IEEE/ASME Transactions on Mechatronics 25, no. 3 (June 2020): 1243–54. https://doi.org/10.1109/TMECH.2020.2971503

[2] Riaz, Saleem, Hassan Elahi, Kashif Javaid, and Tufail Shahzad. "Vibration Feature Extraction and Analysis for Fault Diagnosis of Rotating Machinery - A Literature Survey." Asia Pacific Journal of Multidisciplinary Research 5, no. 1 (2017): 103–110

[3] Caesarendra, Wahyu, and Tegoeh Tjahjowidodo. “A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing.” Machines 5, no. 4 (December 2017): 21. https://doi.org/10.3390/machines5040021

[4] Tian, Jing, Carlos Morillo, Michael H. Azarian, and Michael Pecht. “Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis.” IEEE Transactions on Industrial Electronics 63, no. 3 (March 2016): 1793–1803. https://doi.org/10.1109/TIE.2015.2509913

[5] Li, Yifan, Xin Zhang, Zaigang Chen, Yaocheng Yang, Changqing Geng, and Ming J. Zuo. “Time-Frequency Ridge Estimation: An Effective Tool for Gear and Bearing Fault Diagnosis at Time-Varying Speeds.” Mechanical Systems and Signal Processing 189 (April 2023): 110108. https://doi.org/10.1016/j.ymssp.2023.110108

Helper Function

getShortenedLabels – This function shortens the labels for better display on confusion charts.

function shortenedLabels = getShortenedLabels(labels)
%   This function is only intended support examples in the Signal
%   Processing Toolbox. It may be changed or removed in a future release

shortenedLabels = string(size(labels));
labels = string(labels);

for idx=1:numel(labels)
    if labels(idx) == "HealthySignal"
        str2erase = "Signal";
    else
        str2erase = "Fault";
    end
    shortenedLabels(idx) = erase(labels(idx),str2erase);
end

shortenedLabels = categorical(shortenedLabels);
shortenedLabels = shortenedLabels(:);
end