Main Content

NLMEResults

Results object containing estimation results from nonlinear mixed-effects modeling

expand all in page

Description

The NLMEResults object contains estimation results from fitting a nonlinear mixed-effects model using sbiofitmixed.

Creation

Use the sbiofitmixed function to create an NLMEResults object.

Properties

expand all

Table of the estimated fixed effects and their standard errors, specified as a table.

Table of the estimated random effects for each group, specified as a table.

Table of estimated parameter values, including fixed and random effects, specified as a table.

Table of estimated parameter values, including only fixed effects, specified as a table.

Table of the covariance matrix of the random effects, specified as a table.

Statistics returned by the nlmefit (Statistics and Machine Learning Toolbox) and nlmefitsa (Statistics and Machine Learning Toolbox) algorithm, specified as a structure array.

Covariate names, specified as a cell array of character vectors.

Data used for fitting, specified as a groupedData object.

This Data property contains a copy of groupedData specified as the input data in the sbiofitmixed call or the Data property of a fitproblem object.

Estimated parameter names, specified as a cell array of character vectors.

Table describing the error models and estimated error model parameters, specified as a table.

The table has one row with three variables: ErrorModel, a, and b. The ErrorModel variable is categorical. The variables a and b can be NaN when they do not apply to a particular error model.

There are four built-in error models. Each model defines the error using a standard mean-zero and unit-variance (Gaussian) variable e, the function value f, and one or two parameters a and b. In SimBiology®, the function f represents simulation results from a SimBiology model.

  • 'constant': y=f+ae

  • 'proportional': y=f+b|f|e

  • 'combined': y=f+(a+b|f|)e

  • 'exponential': y=f∗exp(ae)

Name of the estimation function, specified as 'nlmefit' or 'nlmefitsa'.

Maximized loglikelihood for the fitted model, specified as a scalar.

Akaike Information Criterion (AIC), specified as a scalar. The AIC is calculated as AIC = 2*(-LogLikelihood + P), where P is the number of parameters. For details, see nlmefit (Statistics and Machine Learning Toolbox).

Bayes Information Criterion (BIC), specified as a scalar. The BIC is calculated as BIC = -2*LogLikelihood + P*log(N), where N is the number of observations or groups, and P is the number of parameters. For details, see nlmefit (Statistics and Machine Learning Toolbox).

Degrees of freedom for error (DFE), specified as a scalar. The DFE is calculated as DFE = N-P, where N is the number of observations and P is the number of parameters.

Note

If you are using the nlmefitsa method, Loglikelihood, AIC, and BIC properties are empty by default. To calculate these values, specify the 'LogLikMethod' option of nlmefitsa (Statistics and Machine Learning Toolbox) when you run sbiofitmixed as follows.

opt.LogLikMethod = 'is';
fitResults = sbiofitmixed(...,'nlmefitsa',opt);

Object Functions

boxplotCreate box plot showing the variation of estimated SimBiology model parameters
covariateModelReturn a copy of the covariate model that was used for the nonlinear mixed-effects estimation using sbiofitmixed
fitted Return the simulation results of a fitted nonlinear mixed-effects model
plotCompare simulation results to the training data, creating a time-course subplot for each group
plotActualVersusPredictedCompare predictions to actual data, creating a subplot for each response
plotResidualDistributionPlot the distribution of the residuals
plotResidualsPlot the residuals for each response, using the time, group, or prediction as the x-axis
predictSimulate and evaluate fitted SimBiology model
randomSimulate a SimBiology model, adding variations by sampling the error model

Examples

collapse all

Open Live Script

This example uses data collected on 59 preterm infants given phenobarbital during the first 16 days after birth [1]. Each infant received an initial dose followed by one or more sustaining doses by intravenous bolus administration. A total of between 1 and 6 concentration measurements were obtained from each infant at times other than dose times, for a total of 155 measurements. Infant weights and APGAR scores (a measure of newborn health) were also recorded.

Load the data. 

load pheno.mat ds

Convert the dataset to a groupedData object, a container for holding tabular data that is divided into groups. It can automatically identify commonly used variable names as the grouping variable or independent (time) variable. Display the properties of the data and confirm that GroupVariableName and IndependentVariableName are correctly identified as 'ID' and 'TIME', respectively. 

data = groupedData(ds);
data.Properties
ans = struct with fields:
                Description: ''
                   UserData: []
             DimensionNames: {'Observations'  'Variables'}
              VariableNames: {'ID'  'TIME'  'DOSE'  'WEIGHT'  'APGAR'  'CONC'}
              VariableTypes: ["double"    "double"    "double"    "double"    "double"    "double"]
       VariableDescriptions: {}
              VariableUnits: {}
         VariableContinuity: []
                   RowNames: {}
           CustomProperties: [1x1 matlab.tabular.CustomProperties]
          GroupVariableName: 'ID'
    IndependentVariableName: 'TIME'

Create a simple one-compartment PK model with bolus dosing and linear clearance to fit such data. Use the PKModelDesign object to construct the model. Each compartment is defined by a name, dosing type, a clearance type, and whether or not the dosing requires a lag parameter. After constructing the model, you can also get a PKModelMap object map that lists the names of species and parameters in the model that are most relevant for fitting. 

pkmd = PKModelDesign;
addCompartment(pkmd,'Central','DosingType','Bolus',...
                    'EliminationType','linear-clearance',...
                    'HasResponseVariable',true,'HasLag',false);
[onecomp, map] = pkmd.construct;

Describe the experimentally measured response by mapping the appropriate model component to the response variable. In other words, indicate which species in the model corresponds to which response variable in the data. The PKModelMap property Observed indicates that the relevant species in the model is Drug_Central, which represents the drug concentration in the system. The relevant data variable is CONC, which you visualized previously. 

map.Observed
ans = 1x1 cell array
    {'Drug_Central'}

Map the Drug_Central species to the CONC variable. 

responseMap = 'Drug_Central = CONC';

The parameters to estimate in this model are the volume of the central compartment Central and the clearance rate Cl_Central. The PKModelMap property Estimated lists these relevant parameters. The underlying algorithm of sbiofit assumes parameters are normally distributed, but this assumption may not be true for biological parameters that are constrained to be positive, such as volume and clearance. Specify a log transform for the estimated parameters so that the transformed parameters follow a normal distribution. Use an estimatedInfo object to define such transforms and initial values (optional). 

map.Estimated
ans = 2x1 cell
    {'Central'   }
    {'Cl_Central'}

Define such estimated parameters, appropriate transformations, and initial values. 

estimatedParams = estimatedInfo({'log(Central)','log(Cl_Central)'},'InitialValue',[1 1]);

Each infant received a different schedule of dosing. The amount of drug is listed in the data variable DOSE. To specify these dosing during fitting, create dose objects from the data. These objects use the property TargetName to specify which species in the model receives the dose. In this example, the target species is Drug_Central, as listed by the PKModelMap property Dosed. 

map.Dosed
ans = 1x1 cell array
    {'Drug_Central'}

Create a sample dose with this target name and then use the createDoses method of groupedData object data to generate doses for each infant based on the dosing data DOSE. 

sampleDose = sbiodose('sample','TargetName','Drug_Central');
doses = createDoses(data,'DOSE','',sampleDose);

Fit the model. 

[nlmeResults,simI,simP] = sbiofitmixed(onecomp,data,responseMap,estimatedParams,doses,'nlmefit');

Visualize the fitted results using individual-specific parameter estimates. 

plot(nlmeResults,'ParameterType','individual');

Figure contains 65 axes objects. Axes object 1 is empty. Axes object 2 is empty. Axes object 3 is empty. Axes object 4 is empty. Axes object 5 is empty. Axes object 6 with title 59 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 7 with title 58 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 8 with title 57 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 9 with title 56 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 10 with title 55 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 11 with title 54 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 12 with title 53 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 13 with title 52 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 14 with title 51 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 15 with title 50 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 16 with title 49 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 17 with title 48 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 18 with title 47 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 19 with title 46 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 20 with title 45 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 21 with title 44 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 22 with title 43 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 23 with title 42 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 24 with title 41 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 25 with title 40 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 26 with title 39 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 27 with title 38 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 28 with title 37 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 29 with title 36 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 30 with title 35 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 31 with title 34 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 32 with title 33 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 33 with title 32 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 34 with title 31 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 35 with title 30 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 36 with title 29 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 37 with title 28 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 38 with title 27 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 39 with title 26 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 40 with title 25 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 41 with title 24 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 42 with title 23 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 43 with title 22 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 44 with title 21 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 45 with title 20 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 46 with title 19 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 47 with title 18 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 48 with title 17 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 49 with title 16 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 50 with title 15 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 51 with title 14 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 52 with title 13 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 53 with title 12 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 54 with title 11 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 55 with title 10 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 56 with title 9 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 57 with title 8 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 58 with title 7 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 59 with title 6 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 60 with title 5 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 61 with title 4 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 62 with title 3 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 63 with title 2 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 64 with title 1 contains 2 objects of type line. One or more of the lines displays its values using only markers Hidden axes object 65 contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Predicted - individual (Predicted - individual.Central.Drug_Central), Observed (Observed.CONC).

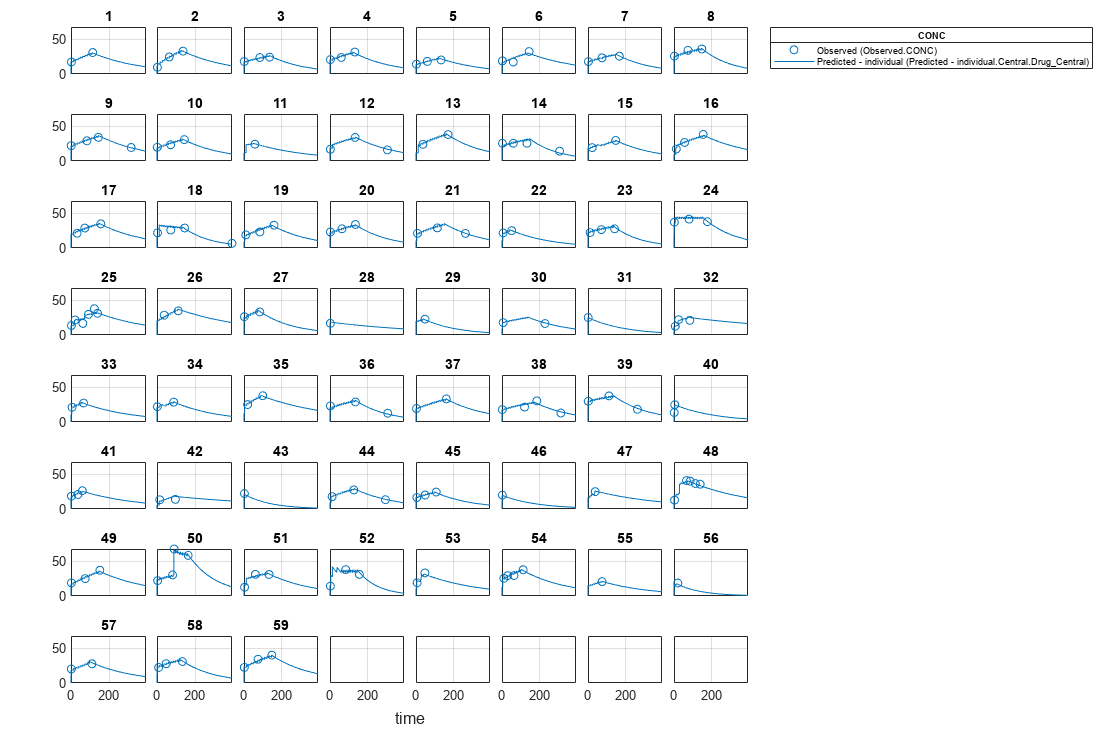
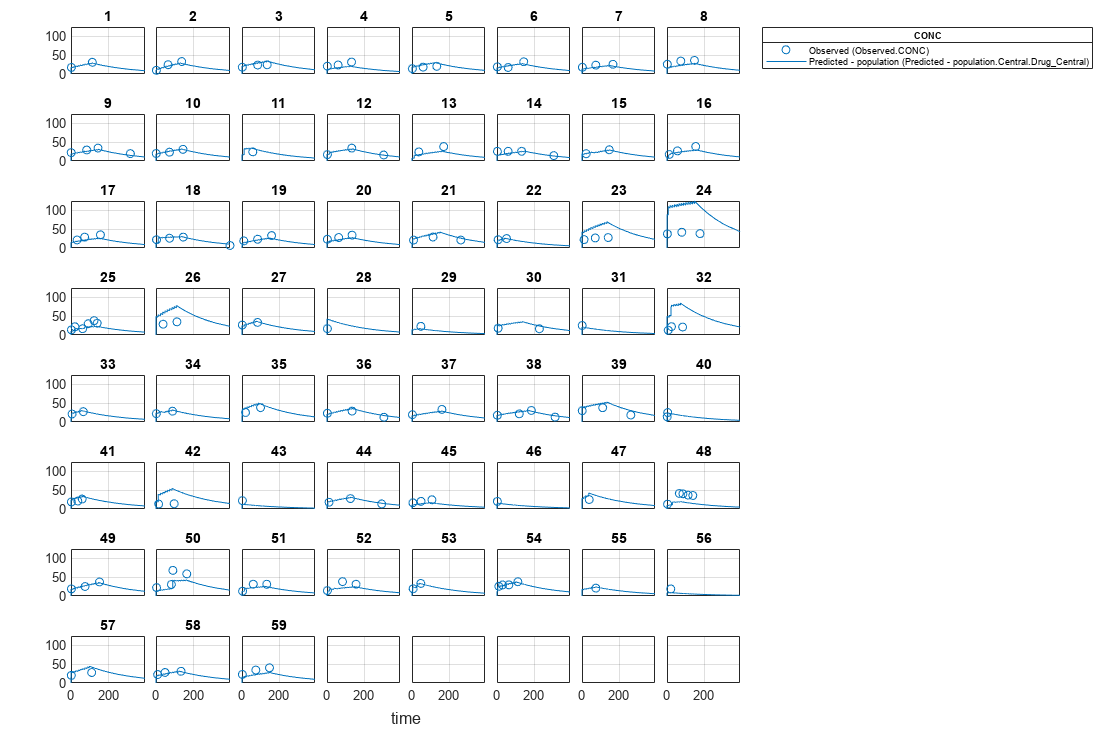
Visualize the fitted results using population parameter estimates. 

plot(nlmeResults,'ParameterType','population');

Figure contains 65 axes objects. Axes object 1 is empty. Axes object 2 is empty. Axes object 3 is empty. Axes object 4 is empty. Axes object 5 is empty. Axes object 6 with title 59 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 7 with title 58 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 8 with title 57 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 9 with title 56 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 10 with title 55 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 11 with title 54 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 12 with title 53 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 13 with title 52 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 14 with title 51 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 15 with title 50 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 16 with title 49 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 17 with title 48 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 18 with title 47 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 19 with title 46 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 20 with title 45 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 21 with title 44 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 22 with title 43 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 23 with title 42 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 24 with title 41 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 25 with title 40 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 26 with title 39 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 27 with title 38 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 28 with title 37 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 29 with title 36 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 30 with title 35 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 31 with title 34 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 32 with title 33 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 33 with title 32 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 34 with title 31 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 35 with title 30 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 36 with title 29 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 37 with title 28 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 38 with title 27 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 39 with title 26 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 40 with title 25 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 41 with title 24 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 42 with title 23 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 43 with title 22 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 44 with title 21 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 45 with title 20 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 46 with title 19 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 47 with title 18 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 48 with title 17 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 49 with title 16 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 50 with title 15 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 51 with title 14 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 52 with title 13 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 53 with title 12 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 54 with title 11 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 55 with title 10 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 56 with title 9 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 57 with title 8 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 58 with title 7 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 59 with title 6 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 60 with title 5 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 61 with title 4 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 62 with title 3 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 63 with title 2 contains 2 objects of type line. One or more of the lines displays its values using only markers Axes object 64 with title 1 contains 2 objects of type line. One or more of the lines displays its values using only markers Hidden axes object 65 contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Predicted - population (Predicted - population.Central.Drug_Central), Observed (Observed.CONC).

Display the variation of estimated parameters using boxplot.

boxplot(nlmeResults)

Figure contains an axes object. The axes object contains 14 objects of type line. One or more of the lines displays its values using only markers

Compare the model predictions to the actual data.

plotActualVersusPredicted(nlmeResults)

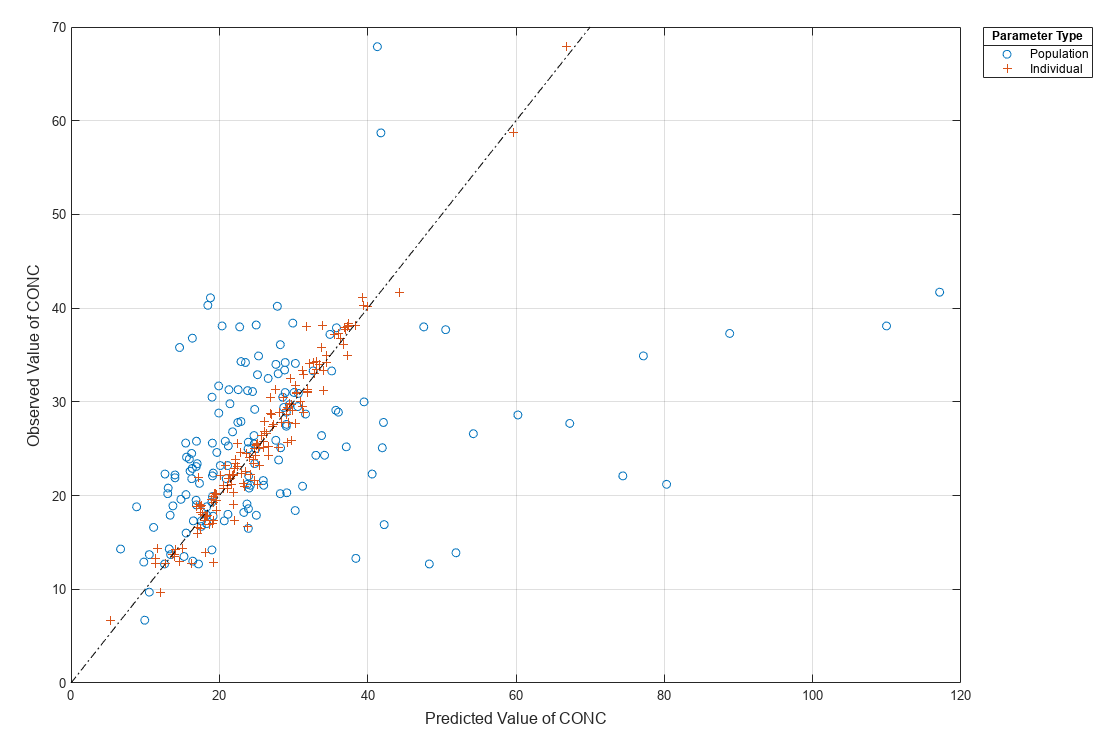
Figure contains 2 axes objects. Axes object 1 contains 3 objects of type line. One or more of the lines displays its values using only markers Hidden axes object 2 contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Individual, Population.

Plot the distribution of residuals.

plotResidualDistribution(nlmeResults)

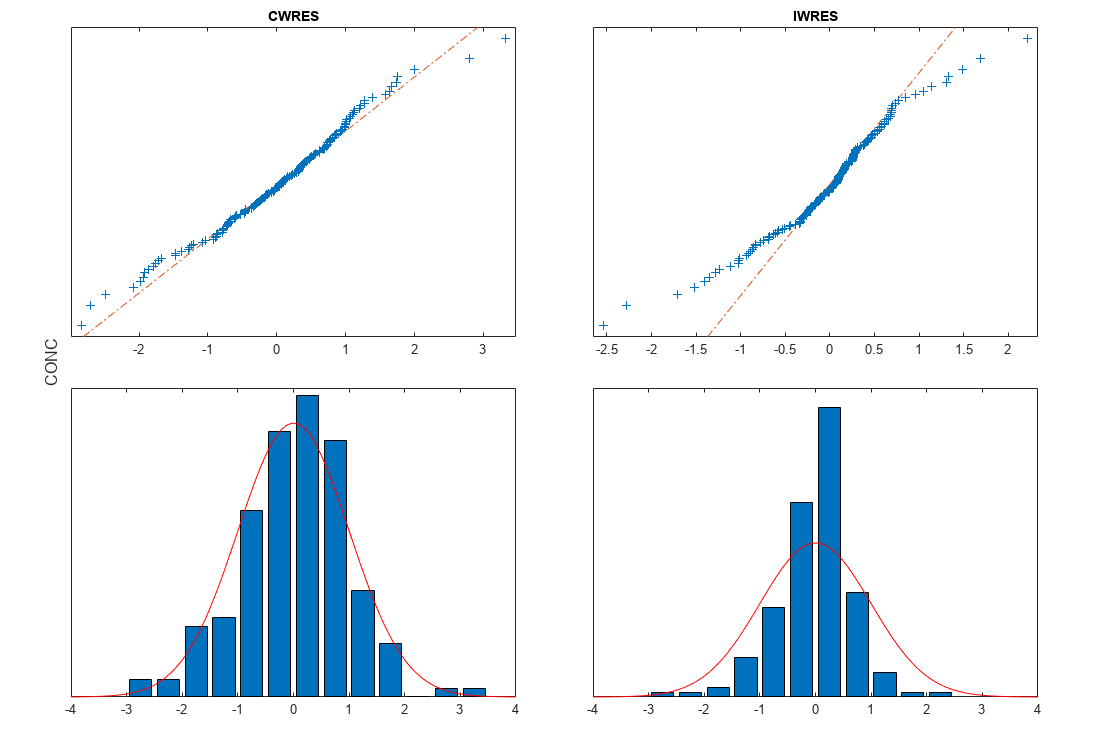
Figure contains 4 axes objects. Axes object 1 contains 2 objects of type bar, line. Axes object 2 contains 2 objects of type bar, line. Axes object 3 with title IWRES contains 3 objects of type line. One or more of the lines displays its values using only markers Axes object 4 with title CWRES contains 3 objects of type line. One or more of the lines displays its values using only markers

Plot residuals for each response using the model predictions on x-axis.

plotResiduals(nlmeResults,'Predictions')

Figure contains 2 axes objects. Axes object 1 contains 3 objects of type line. One or more of the lines displays its values using only markers Hidden axes object 2 contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent IWRES, CWRES.

Version History

Introduced in R2014a

See Also

| | (Statistics and Machine Learning Toolbox) | (Statistics and Machine Learning Toolbox)