Derivative
计算连续输入信号关于时间的逼近连续导数
库:
Simulink /
Continuous
描述
Derivative 模块可逼近连续输入信号 u 关于仿真时间 t 的连续导数。当需要计算具有连续采样时间的可微分信号的导数时,可以使用 Derivative 模块。
Derivative 模块如果使用不当会导致仿真结果不准确。如果可能,请考虑以下几种方案来替代 Derivative 模块:
重新排列系统方程以求解积分而不是导数。然后,根据新方程构建模型,以便软件使用 Integrator 等模块求积分,而不是求微分。
有关示例,请参阅最佳形式的数学模型。
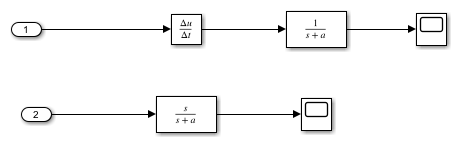
当 Transfer Fcn 模块也作用于 Derivative 模块的输入或输出信号时,改为通过在传递函数中添加零来实现信号的导数。
要计算离散系统中离散信号的有限差分或差商,请使用 Discrete Derivative 模块。
当您必须使用 Derivative 模块时,请仅对其使用具有连续采样时间的可微分输入信号。
当连接到此端口的信号具有离散的或子步中不变的采样时间时,软件会发出警告。 (自 R2023b 起)
当输入信号具有常数采样时间时,软件不会发出警告,但调节信号值会导致输入信号不连续。对这些不连续点求微分会在输出信号中产生尖峰。
要计算离散系统中离散信号的有限差分或差商,请使用 Discrete Derivative 模块。
确保连续导数逼近的准确度
使用 Derivative 模块时,必须确保模块输出信号的准确性满足您的要求。即使在适当的环境下使用,Derivative 模块输出信号的准确性也取决于步长,还可能取决于系统其余部分的动态特性。
使用最大步长参数来防止变步长求解器采用的步长过大而无法满足您的准确性要求。要为最大步长选择合适的值,您可能需要运行几次仿真。
在变步长仿真中,求解器通过监控整个模型中连续状态计算的误差来确定每个主时间步的大小。当连续状态的计算值中的误差超出指定的容差级别时,求解器会减小步长,直到误差在容差范围内。
Derivative 模块没有任何连续状态,因此求解器无法调整步长以确保 Derivative 模块计算满足容差要求。如果求解器在输入信号值快速变化时采用较大的时间步,模块可能会产生意外的输出值。
示例
端口
输入
输出
参数
模块特性
数据类型 |
|
直接馈通 |
|
多维信号 |
|
可变大小信号 |
|
过零检测 |
|
算法
Derivative 模块计算数值差分 以逼近连续导数 ,其中 是输入信号值的变化量, 是求解器达到当前仿真时间所采用的主时间步的大小。连续导数逼近的准确性取决于输入信号的变化率和步长。
Derivative 模块的初始输出值始终为 0。在考虑初始输出值的前提下,下面的方程表示了模块输入和输出信号之间的精确关系。
t 是当前仿真时间。
是仿真中上一个主时间步命中点的时间。