用动画演示倒立摆
此示例说明如何使用 Simulink® 对倒立摆系统建模进行动画演示。倒立摆的质心在枢轴点上方。为了稳定地保持此位置,当钟摆开始下落时,系统执行控制逻辑以将枢轴点移至质心下方。倒立摆是用于测试控制策略的经典动力学问题。
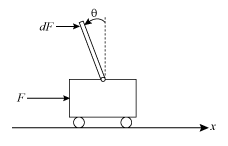
系统
在此示例中,系统由装载在移动小车上的一个倒立摆组成。该模型将运动限制在垂直平面上进行。为了保持系统的稳定性,该模型实现状态反馈控制来跟踪小车的位置。有关方程如何在 Simulink 中推导和实现的说明,请参阅Derive Equations of Motion and Simulate Cart-Pole System (Symbolic Math Toolbox)。
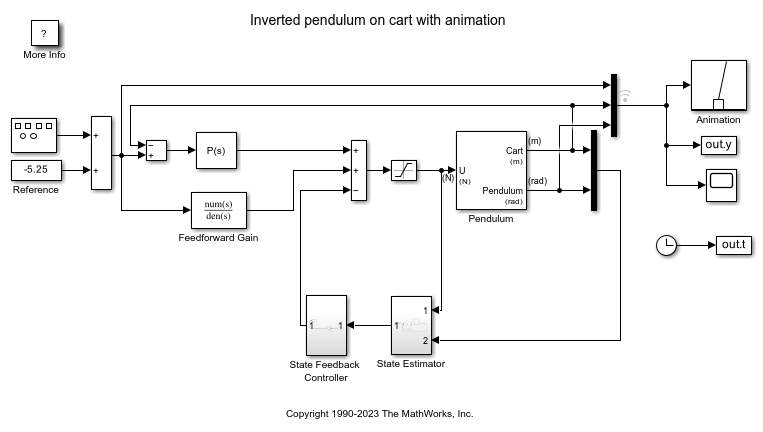
动画
该模型使用一个 Level-2 MATLAB S-Function 模块来实现动画。S-Function 使用 MATLAB® Handle Graphics®。要查看 S-Function,请打开 pendan.m。

倒立摆动力学
该模型使用封装子系统来实现倒立摆的非线性系统动力学。该子系统确定小车沿 x 轴的位置以及摆绕枢轴点的旋转。

状态反馈控制
该模型实现状态反馈控制以跟踪小车的位置并保持枢轴点低于摆的质心。State Estimator 子系统使用龙伯格观测器模型来估计系统的内部状态。
分析
Scope 模块在仿真运行时提供信号输出。您也可以使用仿真数据检查器来调查记录的信号。

另请参阅
Level-2 MATLAB S-Function | Discrete PID Controller | Signal Generator
主题
- Add App Designer App to Inverted Pendulum Model (Simulink Real-Time)
- Derive Equations of Motion and Simulate Cart-Pole System (Symbolic Math Toolbox)
- 小车倒立摆的控制 (Control System Toolbox)
- Inverted Pendulum Controller Tuning (Simulink Design Optimization)
- 封装基础知识
- 使用信号记录保存信号数据
- Simulink 模型中的单位指定