一般应用领域
Simulink® 可让您对各种动态系统进行建模和仿真。下列示例模型说明从简单到复杂的各种一般应用。
精选示例
弹球的仿真
此示例使用一个弹球的两个模型来说明对具有 Zeno 行为的混合动态系统进行建模的不同方法。一般来说，Zeno 行为的特征可非正式地表示为某些混合系统在有限时间间隔内发生无限数量的事件。球在失去能量的同时，球与地面发生碰撞的时间间隔越来越短。
Analyze Impact of Model Parameters on Bouncing Ball Simulation
Analyzes the impact of the damping coefficient on a mass-spring-damper model of the dynamics of a bouncing ball. After running a simulation using a vectorized parameter value, the example analyzes the effect of varying the parameter by exploring these questions:
单液压缸仿真
此示例说明如何使用 Simulink® 对液压缸进行建模。您可以将这些概念应用于需要液压行为建模的应用中。
房屋的热模型
此示例说明如何使用 Simulink® 来创建房屋的热模型。此系统对室外环境、房屋的热特性和房屋供暖系统进行建模。
Approximating Nonlinear Relationships: Type S Thermocouple
Approximate nonlinear relationships of a type S thermocouple.
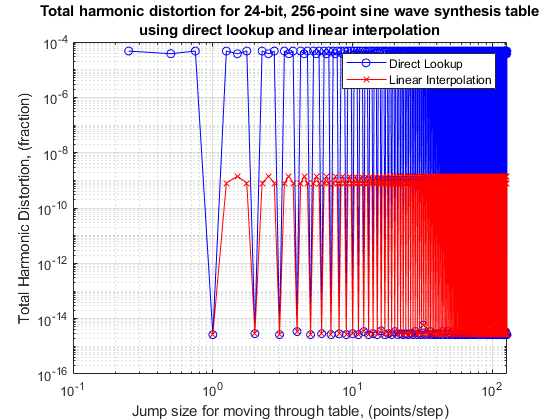
Digital Waveform Generation: Approximate a Sine Wave
Design and evaluate a sine wave data table for use in digital waveform synthesis applications in embedded systems and arbitrary waveform generation instruments.
精确的过零检测
此示例显示过零检测在 Simulink® 中的工作原理。Simulink 使用过零检测来精确仿真突然的模型变化或不连续性，而不会减少求解器时间步。有关详细信息，请参阅过零检测。
Spiral Galaxy Formation Simulation Using MATLAB Function Blocks
Use MATLAB Function blocks to simulate and plot galaxy interactions.
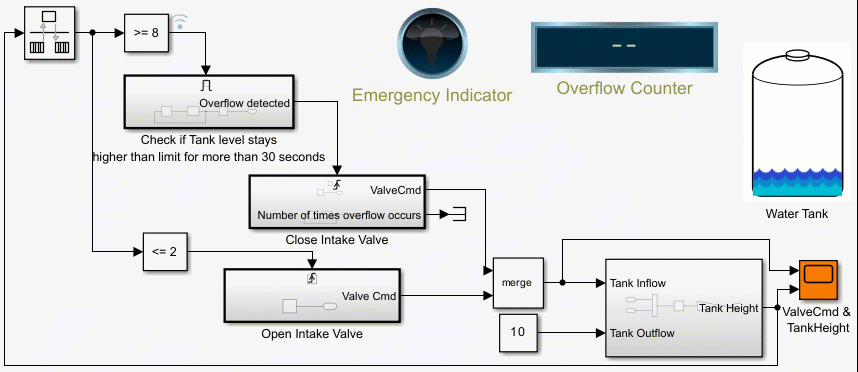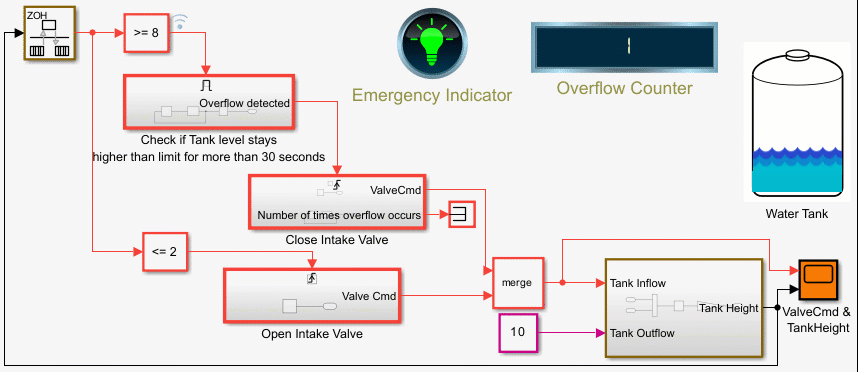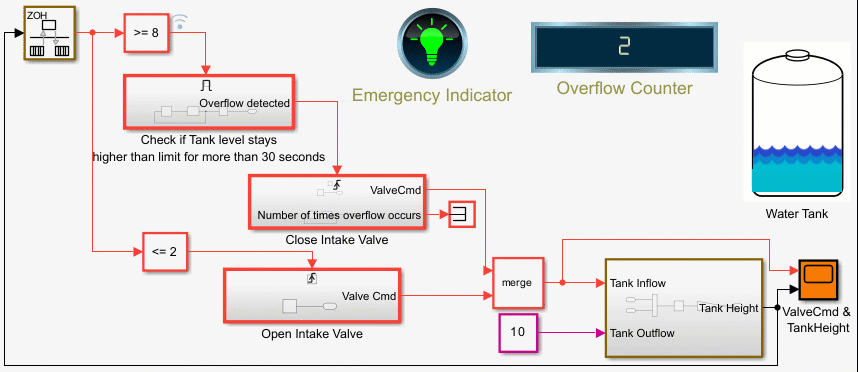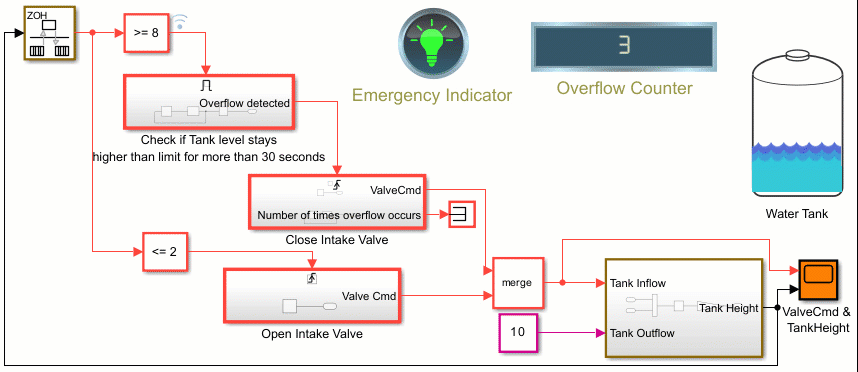
Counters Using Conditionally Executed Subsystems
Implement counters using Enabled and Triggered subsystems. In this example, the model sldemo_counters controls flow of water into a tank and uses a counter to count the number of times overflow occurs, where overflow occurs when the water level in the tank is 8 meters or more for 30 seconds or more.
质量-弹簧-阻尼器系统中的粘滑摩擦和硬限位模型
此示例说明了一种方法，您可以使用该方法将来自粘滑运动的硬限位和摩擦变化合并到一个质量-弹簧-阻尼器模型中。
使用时序逻辑的 Bang-Bang 控制
此示例说明如何使用 Stateflow® 为锅炉的 Bang-Bang 温度控制系统建模。在 Simulink® 中对锅炉动态特性进行建模。
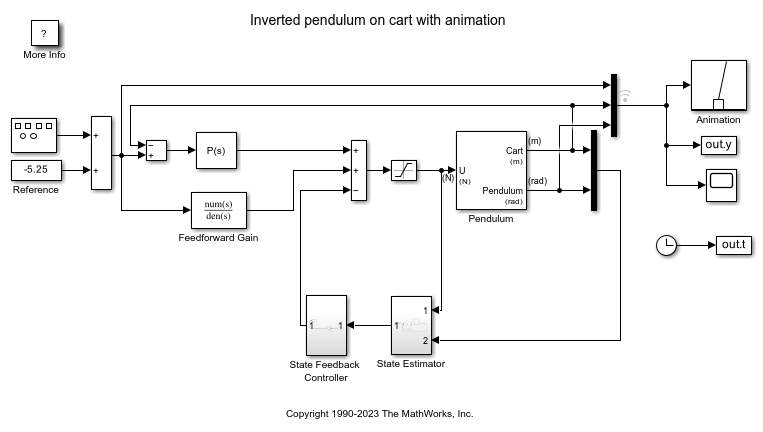
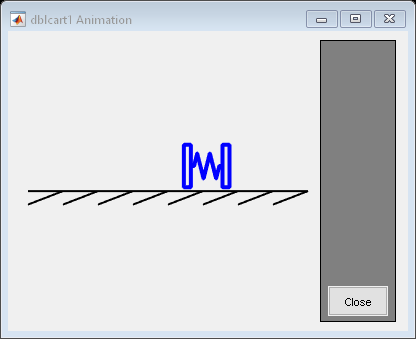
用动画演示倒立摆
此示例说明如何使用 Simulink® 对倒立摆系统建模进行动画演示。倒立摆的质心在枢轴点上方。为了稳定地保持此位置，当钟摆开始下落时，系统执行控制逻辑以将枢轴点移至质心下方。倒立摆是用于测试控制策略的经典动力学问题。
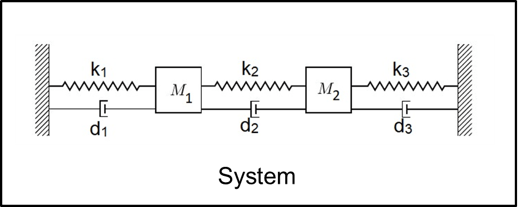
双弹簧质量系统
此示例说明如何对一个具有周期性变化的外力函数的双弹簧-质量-阻尼系统建模。模型使用 S-Function 模块在仿真期间以动画方式显示质量系统。在该系统中，唯一的传感器连接到左侧的质量模块上，作动器也连接到左侧的质量模块上。该示例使用状态估计和线性二次调节器 (LQR) 控制。
用动画演示填充和排空水箱
此示例说明如何对水箱中的液体动态建模。模型仿真液体入流和出流。
仿真具有可变传输延迟现象的系统
此示例说明您可以使用 Simulink® 对可变传输延迟现象进行建模的两种情况。
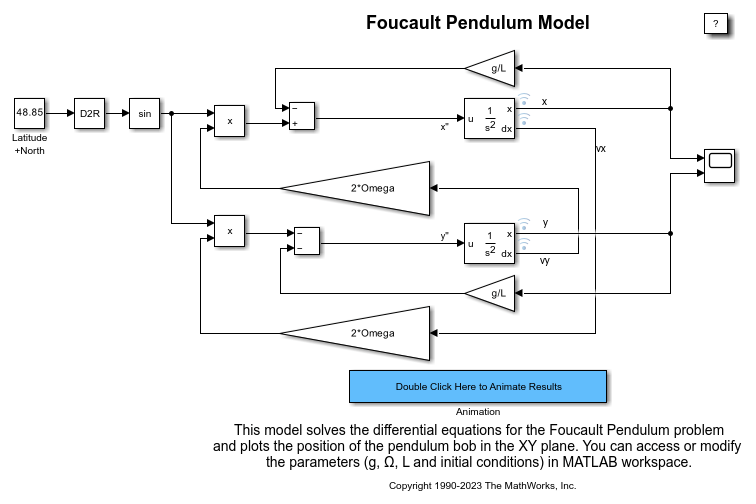
Foucault Pendulum Model
Model a Foucault pendulum. The Foucault pendulum was the brainchild of the French physicist Leon Foucault. It was intended to prove that Earth rotates around its axis. The oscillation plane of a Foucault pendulum rotates throughout the day as a result of axial rotation of the Earth. The plane of oscillation completes a whole circle in a time interval T, which depends on the geographical latitude.
使用 Simulink 3D Animation 的傅科摆模型
此示例说明如何在 Simulink® 3D Animation™ 环境中以动画方式显示Foucault Pendulum Model。您可以通过更改模型中的 Latitude 常量值和 MATLAB® 工作区中的其他参数来修改摆位置。
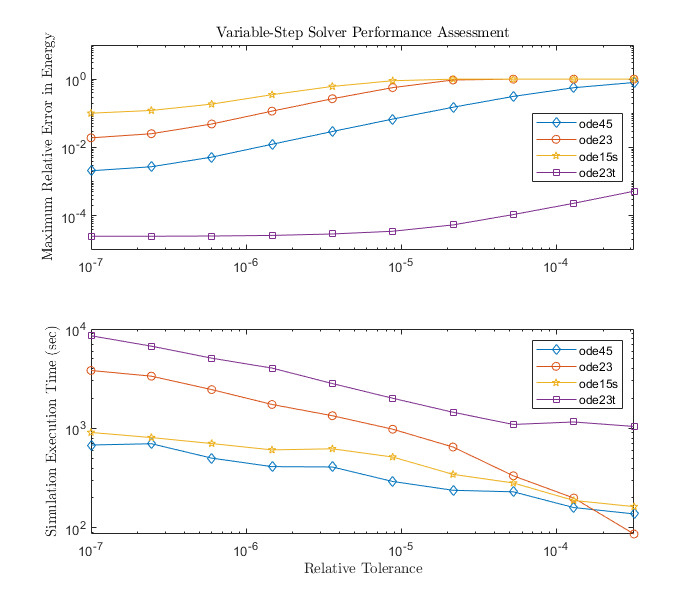
Explore Variable-Step Solvers with Stiff Model
The behavior of variable-step solvers in a Foucault pendulum model. Simulink® solvers ode45, ode15s, ode23, and ode23t are used as test cases. Stiff differential equations are used to solve this problem. There is no exact definition of stiffness for equations. Some numerical methods are unstable when used to solve stiff equations and very small step sizes are required to obtain a numerically stable solution to a stiff problem. A stiff problem may have a fast changing component and a slow changing component.
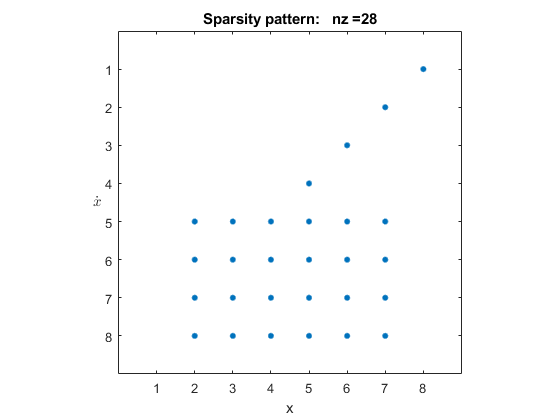
Exploring the Solver Jacobian Structure of a Model
The example shows how to use Simulink® to explore the solver Jacobian sparsity pattern, and the connection between the solver Jacobian sparsity pattern and the dependency between components of a physical system. A Simulink model that models the synchronization of three metronomes placed on a free moving base are used.
Double Bouncing Ball: Use of Adaptive Zero-Crossing Location
Choose the correct zero-crossing location algorithm, based on the system dynamics. For Zeno dynamic systems, or systems with strong chattering, you can select the adaptive zero-crossing detection algorithm through the Configure pane:
四液压缸仿真
使用 Simulink 创建一个具有四个液压缸的模型。该模型有一个泵和四个作动器。
具有载荷约束的双缸模型
使用 Simulink 来对支撑连接两个液压作动器的大质量刚性杆建模。该模型消除了弹簧，因为它将活塞力直接施加于负载。
信息物理系统建模
对变速传送带中的传输延迟进行建模。
Power Analysis of Spring-Mass-Damper System
Analyze mechanical power of mass-spring damper system.
范德波尔振荡器
此示例说明如何在 Simulink® 中对二阶范德波尔 (VDP) 微分方程进行建模。在动力学中，VDP 振荡器不是守恒的，且具有非线性阻尼。在高振幅时，振荡器耗散能量。在低振幅时，振荡器生成能量。振荡器由以下二阶微分方程给出：
Collision Avoidance and Trajectory Tracking of a Marine Vessel
Follow a pre-defined trajectory and avoid collisions.
