串联 RLC 电路建模
物理系统可以描述为一系列隐式形式的微分方程 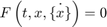 ,或隐式状态空间形式的微分方程
,或隐式状态空间形式的微分方程 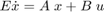
如果 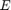 是非奇异矩阵,则该方程组可以轻松转换为常微分方程组 (ODE),并按如下方式求解:
是非奇异矩阵,则该方程组可以轻松转换为常微分方程组 (ODE),并按如下方式求解:
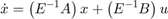
很多时候,系统的状态与其导数没有直接关系,通常表示物理守恒定律。例如:
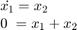
在本例中,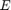 是奇异矩阵,无法求逆。这类方程组通常称为描述符方程组,方程称为微分代数方程 (DAE)。
是奇异矩阵,无法求逆。这类方程组通常称为描述符方程组,方程称为微分代数方程 (DAE)。
串联 RLC 电路
假设有如下简单的串联 RLC 电路。

根据基尔霍夫的电压定律,电路中的压降等于每个元件中的压降之和:
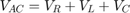
根据基尔霍夫的电流定律:
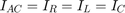
其中下标 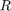 、
、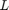 和
和 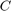 分别表示电阻器、电感和电容。
分别表示电阻器、电感和电容。
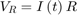
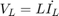 或
或 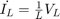
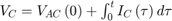 或
或 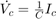
以隐式状态空间形式
在 Simulink® 中用 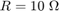 、
、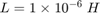 、
、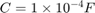 对系统建模,以找到电阻器两端的电压
对系统建模,以找到电阻器两端的电压 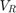 。要使用 Descriptor State-Space 模块,方程组可以编写为隐式(或描述符)状态空间形式
。要使用 Descriptor State-Space 模块,方程组可以编写为隐式(或描述符)状态空间形式 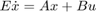 ,如下所示。
,如下所示。

其中 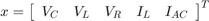 是状态向量。
是状态向量。
设置 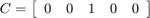 ,因为正在测量电阻器中的电压。
,因为正在测量电阻器中的电压。
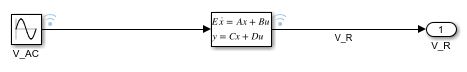
将此项与用代数环对系统建模进行比较,以便找到 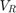 。
。

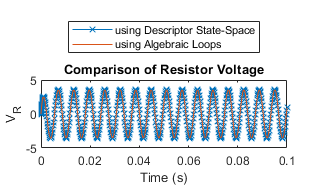
两个模型的仿真得到相同的结果。但是,Descriptor State-Space 模块允许您生成更简单的模块图,并避免代数环。