机械臂的滑动模式控制设计

自 R2024b 起

此示例说明如何使用滑动模式控制 (SMC) 为具有两个驱动关节的机械臂设计控制器。SMC 适用于在存在扰动和模型不确定性的情况下仍需要保持稳健性的系统。使用 SMC，即使在存在外部扰动和参数变化的情况下，也可以实现对所需轨迹的高精度跟踪。有关 SMC 的详细信息，请参阅Sliding Mode Control。

机械臂的动态特性

假设有由以下动态方程控制的双关节机械臂的动态特性。

$M (q) q_{}^{¨} + C (q, q_{}^{˙}) q_{}^{˙} + G (q) + F (q_{}^{˙}) = τ + τ_{d}$

其中：

$q$ 、 $\dot{q}$ 和 $\ddot{q}$ 均为 2×1 向量，分别表示关节角度、速度和加速度。
控制输入 $τ$ 是施加到关节的 2×1 扭矩向量。
惯性矩阵 $M (q)$ 、科里奥利力矩阵 $C (q, \dot{q})$ 、重力向量 $G (q)$ 和摩擦向量 $F (\dot{q})$ 封装了机械臂的动态特性。
$τ_{d}$ 表示影响系统的扰动扭矩。

为了便于控制设计，需要定义状态变量 $x_{1} = q$ 和 $x_{2} = \dot{q}$ ，并定义控制输入 $u = τ$ 。然后定义更紧凑的系统状态空间表示 $\dot{x} = f (x) + g (x) u$ 。

状态向量 $x (t)$ 由下式给出：

$x (t) = [\begin{array}{c} q \\ \dot{q} \end{array}]$ ，其中 $q = [\begin{array}{c} θ_{1} \\ θ_{2} \end{array}]$

在本例中， $f (x, t) = [\begin{array}{c} \dot{q} \\ {M (q)}^{- 1} [τ_{d} - C (q, \dot{q}) \dot{q} - G (q) - F (\dot{q})] \end{array}]$ 并且 $g (x, t) = [\begin{array}{c} 0_{2 x2} \\ {M (q)}^{- 1} \end{array}]$

机械臂动态特性在 robotStateFcn 辅助函数中实现。此函数基于当前状态向量 $x$ 、控制输入向量 $u$ 和模型参数向量生成关于时间的状态导数。对于此示例，假设摩擦力模型 $F (\dot{q})$ 可忽略不计且不用于计算。

对于此示例，定义机械臂的以下参数。

M = [0.5; 1.5]; % Masses of the first and second links (kg)
L = [1.0; 0.8]; % Lengths of the first and second link (m)
J = [5.0; 5.0]; % Moments of inertia of the first and second link (kgm^2)

机械臂的参考轨迹

在此示例中，机械臂的两个驱动关节的参考轨迹由时变指数函数描述。

$θ_{1, 2} = a_{1, 2} + b_{1, 2} e^{d_{1, 2} t} + c_{1, 2} e^{e_{1, 2} t}$

参考轨迹主要针对设定点 $a_{1, 2}$ ，其他项确保从初始位置到这些设定点的平滑过渡。这些函数的微分对于产生一致的速度和加速度曲线至关重要，有助于机械臂的稳定性和精确运动。这一特性还有助于使用需要连续且可微分的设定点的控制算法。

对于此示例，同时设置两个关节的参考轨迹的参数。这些参数定义了轨迹函数随时间变化的形状和行为。

[a1,b1,c1,d1,e1] = deal(1,-1,0.25,-1,-4);
[a2,b2,c2,d2,e2] = deal(1,1,-0.3,-1,-3);

绘制两个关节的参考轨迹，以可视化指定时间间隔内的目标位置。

qref = @(time,a,b,c,d,e) a + b*exp(d*time) + c*exp(e*time);
time = linspace(0,10);

figure
tiledlayout(2,1)

nexttile
plot(time,qref(time,a1,b1,c1,d1,e1))
title("Reference Trajectory for Joint 1")
ylabel("Position (rad)")
xlabel("Time (s)")

nexttile
plot(time,qref(time,a2,b2,c2,d2,e2))
title("Reference Trajectory for Joint 2")
ylabel("Position (rad)")
xlabel("Time (s)")

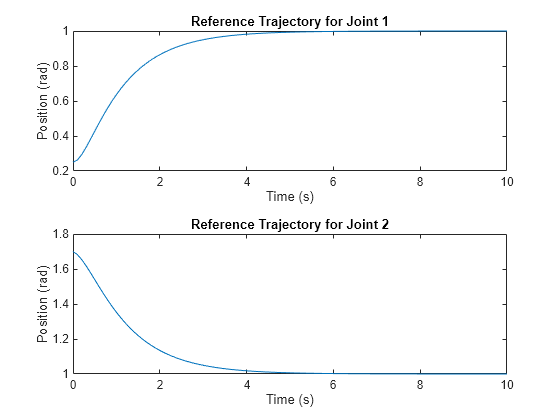
Figure contains 2 axes objects. Axes object 1 with title Reference Trajectory for Joint 1, xlabel Time (s), ylabel Position (rad) contains an object of type line. Axes object 2 with title Reference Trajectory for Joint 2, xlabel Time (s), ylabel Position (rad) contains an object of type line.

设计滑动模式控制器

SMC 是一种稳健控制策略，它强制系统状态收敛到预定义的滑动面，并随后保持这种状态。这个目标是通过应用不连续控制动作来实现的，该动作根据系统相对于滑动面的位置进行切换。

在此示例中，使用的 SMC 控制律为：

$u = {(C^{T} g (x))}^{- 1} (C^{T} {\ddot{x}}_{d} - C^{T} f (x) + h (s (x)))$

其中：

$h (s (x)) = - η θ (s) - Ks$ 对应于指数趋近律。
$θ (s) = {\begin{cases} 1 & s > ϕ \\ \frac{1}{ϕ} & | s | \leq ϕ \\ - 1 & s < ϕ \end{cases}$ 对应于边界层函数。
$s (x) = C^{T} (x_{d} - x)$ 对应于切换函数。

控制取决于以下参数。

$η$ :不连续控制动作的振幅，增强面对扰动的稳健性。
$k$ :控制律连续部分的比例增益，减少稳态误差并缩短响应时间。
$C$ :滑动面中的系数，影响向滑动面的收敛速度。

$f$ 和 $g$ 项取决于机械臂参数。在实际场景中，您可能无法确切知道这些参数，而只能获得估计值。

$f (x, t) = [\begin{array}{c} \dot{q} \\ {\hat{M} (q)}^{- 1} [τ_{d} - \hat{C} (q, \dot{q}) \dot{q} - \hat{G} (q) - \hat{F} (\dot{q})] \end{array}]$

$g (x, t) = [\begin{array}{c} 0_{2 x2} \\ {\hat{M} (q)}^{- 1} \end{array}]$

其中，机械臂惯性矩阵 $\hat{M} (q)$ 、科里奥利力矩阵 $\hat{C} (q, \dot{q})$ 、摩擦力向量 $\hat{F} (\dot{q})$ 和重力向量 $\hat{G} (q)$ 均为估计值。

对于此示例，定义以下 SMC 控制器参数。

eta = [1; 3];           % Amplitude of discontinuous control action
K = [2; 1];             % Proportional gain
C = [5*eye(2); eye(2)]; % Sliding surface coefficient
Phi = 0.01;             % Boundary layer thickness

使用 SMC 控制器进行闭环仿真

为了评估所设计的 SMC 控制器的性能，在 Simulink® 中对机械臂进行仿真。仿真在参数已知和参数不确定这两种条件下测试控制器的参考跟踪能力。

打开模型。

mdl = "robotManipulatorModel";
open_system(mdl)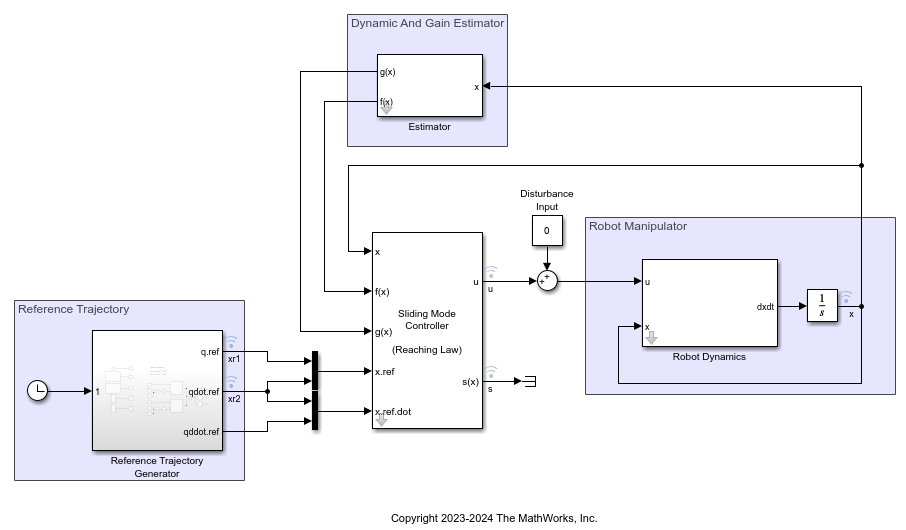

使用符号函数从任意初始位置以零速度开始对系统进行仿真。

定义机械臂的初始状态。

x0 = [0;0;0;0];

选择趋近律和边界层的变体。在本例中，使用 Exponential 趋近律和边界层的 sign 函数。

set_param(mdl+"/Sliding Mode Controller (Reaching Law)", "ReachingLaw", "Exponential");
set_param(mdl+"/Sliding Mode Controller (Reaching Law)", "BoundaryLayer", "Sign");

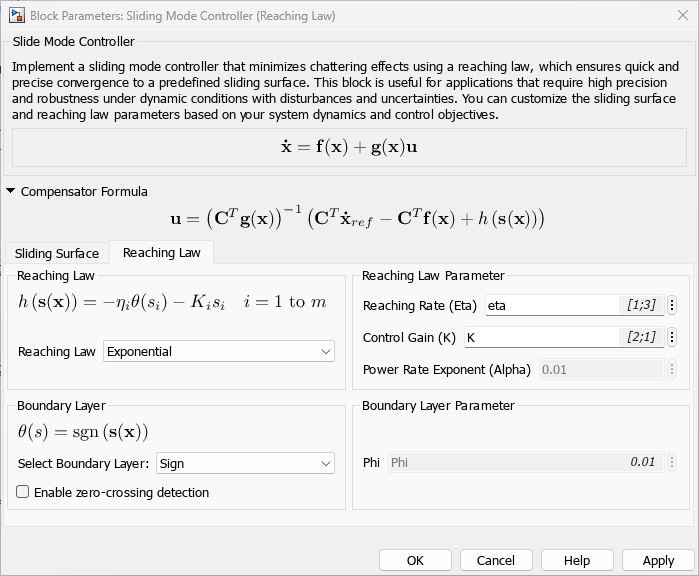
在估计器子系统内设置用于仿真的机械臂动态特性参数，假设机械臂参数已知且不受任何外部扰动的影响。

[Md,Ld,Jd] = deal(M,L,J);

仿真模型。

simout = sim(mdl);

对仿真结果进行后处理以便绘图。

[sim1, ref] = postProcessSimResults(simout);

使用相同的初始条件对系统进行仿真，但使机械臂与估计器子系统之间存在参数不匹配的情况。这样做可以测试 SMC 控制器面对模型不确定性的稳健性。

Md = [0.1; 1.0];
Ld = [1.0; 0.8];
Jd = [4.0; 6.0];

simout = sim(mdl);
sim2 = postProcessSimResults(simout);

绘制仿真结果图。

figure
stackedplot(ref,sim1,sim2, ["q1","q2","qdot1","qdot2"], Title="State Trajectories");

Figure contains an object of type stackedplot. The chart of type stackedplot has title State Trajectories.

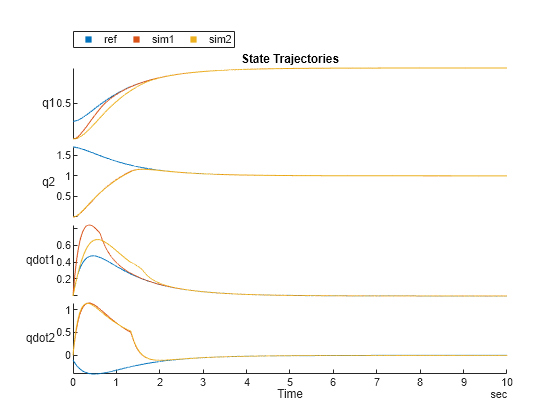
即使在调整参数后，SMC 控制器仍然能够跟踪参考轨迹。

通过绘制控制输入和滑动模式函数来可视化控制器性能。

figure
stackedplot(sim1,sim2, {"Tau1","S1","Tau2","S2"}, Title="Control Inputs and Slide Mode Function Plots");

Figure contains an object of type stackedplot. The chart of type stackedplot has title Control Inputs and Slide Mode Function Plots.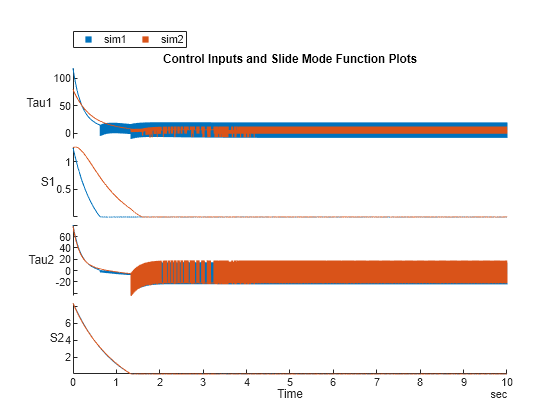

减少控制输入震颤

由于在 SMC 控制器中使用了符号函数，控制输入会出现震颤。减少震颤的一种常见做法是使用饱和函数而不是符号函数。

% switch the controller to use saturation function
set_param(mdl+"/Sliding Mode Controller (Reaching Law)", "BoundaryLayer", "Saturation");

为控制器分配已知的动态参数以进行第一次仿真运行。

[Md,Ld,Jd] = deal(M,L,J);

在设置了饱和函数的情况下执行仿真。

simout = sim(mdl);
[sim3, ref] = postProcessSimResults(simout);

指定不匹配的参数值并对机械臂进行仿真。

Md = [0.1; 1.0];
Ld = [1.0; 0.8];
Jd = [4.0; 6.0];

simout = sim(mdl);
sim4 = postProcessSimResults(simout);

绘制状态轨迹，以将使用饱和函数的控制器的性能与参考轨迹和先前的结果进行比较。

figure
stackedplot(ref,sim1,sim2,sim3,sim4, ["q1","q2","qdot1","qdot2"], Title="State Trajectories")

Figure contains an object of type stackedplot. The chart of type stackedplot has title State Trajectories.

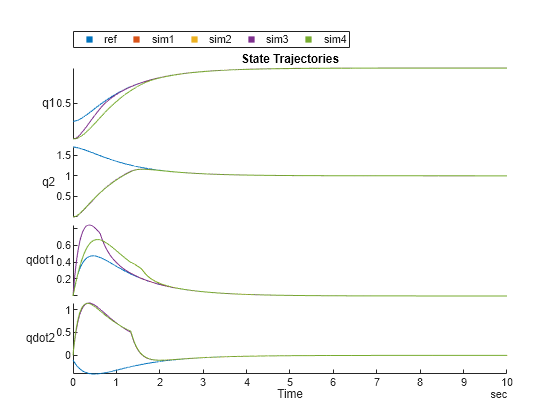
绘制控制输入和滑动模式函数。

figure
stackedplot(sim3,sim4, {"Tau1","S1","Tau2","S2"}, Title="Control Inputs and Slide Mode Function Plots");

Figure contains an object of type stackedplot. The chart of type stackedplot has title Control Inputs and Slide Mode Function Plots.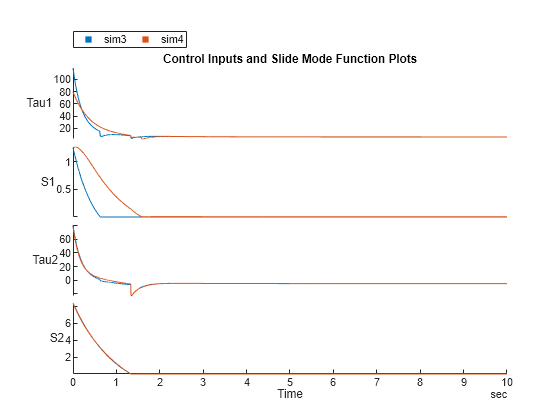

当您在控制律中使用饱和函数时，控制输入中的震颤会显著减少。

减少震颤的另一种方法是使用中继函数而不是符号函数。您可以通过在 Simulink 模型的可变子系统中选择“中继”来试用该函数。

另请参阅

Sliding Mode Controller (Reaching Law)