质量-弹簧-阻尼器系统的滑动模式控制设计

自 R2024b 起

此示例说明如何在命令行和 Simulink® 中实现滑动模式控制 (SMC)。在此示例中，您将为质量-弹簧-阻尼器系统实现 SMC。

滑动模式控制

在 SMC 中，您将定义一个滑动面，系统状态轨迹会收敛到该滑动面并保持在该滑动面上。该滑动面设计为对系统中的扰动和不确定性不敏感。一旦系统状态轨迹位于滑动面上，控制器就会使用反馈控制律将系统状态轨迹沿滑动面驱动至所需状态。有关详细信息，请参阅Sliding Mode Control。

质量-弹簧-阻尼器系统

假设有一个质量为 $M$ 的质量-弹簧-阻尼器系统，该系统连接到刚度系数为 $K$ 的弹簧和阻尼系数为 $D$ 的阻尼器。该系统的动态特性还受到施加在质量上的外部控制力 $F$ 的影响。该力可用作影响系统动态响应的机制。

该系统的微分方程为：

$M \ddot{x} + D \dot{x} + Kx = F$

定义状态变量 $x_{1} = x$ 和 $x_{2} = x_{}^{˙}$ ，这将生成以下描述该系统的一阶微分方程组。

${\begin{cases} {x_{}^{˙}}_{1} = x_{2} \\ {x_{}^{˙}}_{2} = f (x) + g (x) \cdot u (t) \end{cases}$

其中， $f (x) = - \frac{D x_{}^{˙} + K x}{M}$ 表示阻尼器和弹簧作用于质量的固有力， $g (x) = \frac{1}{M}$ 表示控制力 $F$ 对质量的影响，按其幅值归一化。

定义质量-弹簧-阻尼器系统参数，其中质量 $M$ 为 $1 kg$ ，阻尼系数 $D$ 为 $0.1 Ns / m$ ，弹簧常数 $K$ 为 $1 N / m$ 。

param.Mass = 1;      % Mass (kg)
param.Damping = 0.1;   % Damping coefficient (Ns/m)
param.Stiffness = 1; % Spring constant (N/m)

对于此示例，质量-弹簧-阻尼器系统的状态空间函数在 msdStateDer 支持函数中实现。

滑动模式控制设计

对于此示例，将滑动模式函数定义为 $s (t) = ce (t) + \dot{e} (t)$ ，其中 $x_{d}$ 是所需位置， $e = x_{d} - x$ 是跟踪误差。

定义 SMC 控制律如下。

$u = \frac{1}{g} (η sign (s) + ks + c \dot{e} + {\ddot{x}}_{d} - f)$

其中：

$u (t)$ 使用 $s (t)$ 符号来生成不连续控制结构体 ( $u_{k}^{+} (t)$ 和 $u_{k}^{-} (t)$ )。
$η$ 是不连续控制动作的振幅，可增强面对扰动的稳健性。
$k$ 是控制律连续部分的比例增益，可减少稳态误差并缩短响应时间。
$c$ 是滑动面中使用的相同系数，可影响向滑动面的收敛速度。

这种控制输入的选择基于指数趋近律，您可以在其中设置 $\dot{s} = - η sign (s) - ks$ 。然后求解满足此条件的控制输入 [2]。对于 $η$ 和 $k$ 的正值，满足必要充分条件 $s (t) \dot{s} (t) < 0$ 。

设置 SMC 参数，指定控制器设计的控制动作 $η$ 的振幅、比例增益 $k$ 和滑动面系数 $c$ 。对于初始控制器设计，SMC 控制器假设系统中没有扰动 (param.smc.d = 0)。

param.smc.c = 1;
param.smc.k = 1.1;
param.smc.eta = 0.1;
param.smc.d = 0;

对于此示例，SMC 控制输入是使用 smc 支持函数计算的。

对没有扰动的控制器进行仿真

要查看控制器性能，请首先对没有扰动的系统进行仿真。

设置初始条件并定义仿真的时间跨度。

y0 = [1; 0];
tspan = 0:1e-3:10;

创建控制输入函数的句柄。

u = @(x,param) smc(x,param);

使用 ode45 对系统响应进行仿真。

[T,Y] = ode45(@(t,x) msdStateDer(t,x,u,param),tspan,y0);

基于仿真时间计算滑动面和控制输入值。

S = -param.smc.c*Y(:,1) - Y(:,2);
U = smc(Y.',param);

使用 plotResponse 辅助函数可视化随时间变化的系统响应、相平面、控制输入和滑动面。

plotResponse(T,U,Y,S,"System Response without Disturbances")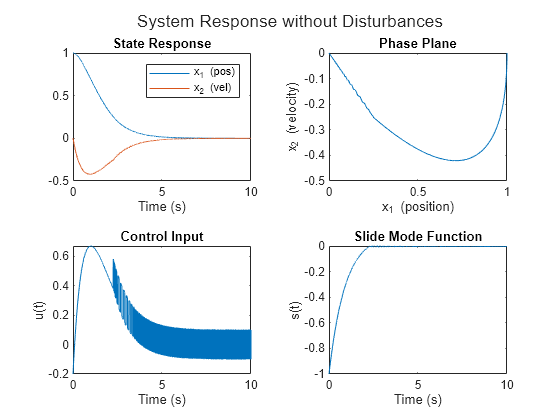

相平面

相平面通过绘制位置对速度的图来直观地表示系统动态特性。在此平面中，系统轨迹收敛到滑动面，滑动面由滑动函数 $s (t) = c e (t) + \dot{e} (t)$ 定义，表示所需的系统行为。当轨迹到达滑动面时，系统处于滑动模式，控制器将系统引导至目标状态。

绘制相平面、系统轨迹和滑动面图。

N = 20;
x1_values = linspace(-0.5,1.5, N);
x2_values = linspace(-1.0,1.0, N);
[X1,X2] = meshgrid(x1_values,x2_values);
XDOT = msdStateDer([],[X1(:), X2(:)].',u,param);

figure
hold on
quiver(X1(:),X2(:),XDOT(1,:).',XDOT(2,:).', ...
    MaxHeadSize=0.1, ...
    AutoScaleFactor=0.9);
plot(Y(:,1),Y(:,2))
plot([-0.5 1.5],-param.smc.c*[-0.5 1.5], ":")
xlim([min(X1(:)) max(X1(:))])
ylim([min(X2(:)) max(X2(:))])
xlabel("x1 (position)")
ylabel("x2 (velocity)")
title("Phase-Plane")
legend("df/dt","States","Slide Surface")

Figure contains an axes object. The axes object with title Phase-Plane, xlabel x1 (position), ylabel x2 (velocity) contains 3 objects of type quiver, line. These objects represent df/dt, States, Slide Surface.

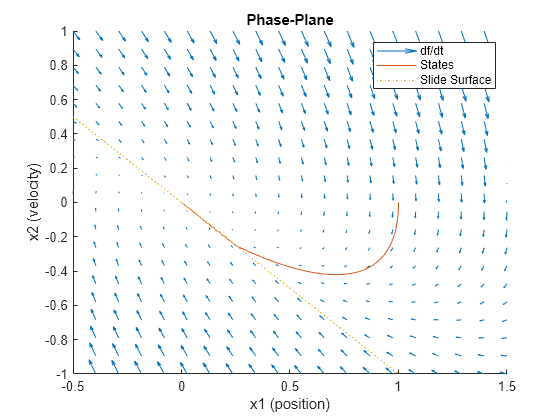
该图直观地描述了质量-弹簧-阻尼器系统响应和滑动模式控制的影响。

对有扰动的系统进行仿真

在实际场景中，系统经常受到外部扰动的影响，这些扰动会影响系统性能。为了测试 SMC 策略的稳健性，可以在质量-弹簧-阻尼器系统仿真中引入扰动。有界扰动被建模为直接影响系统动态特性的时变函数 $d (t)$ ，其中 $| d (t) | \leq D$ 。

对于此示例，假设有一个由下式给出的正弦扰动 $d (t)$ ：

$d (t) = 0.5 \cdot \sin (t)$

SMC 控制律旨在抵消扰动的影响，并将系统状态驱动至所需滑动面。控制律定义如下：

$u = \frac{1}{g} (η sign (s) + ks + c \dot{e} + {\ddot{x}}_{d} - f + D sign (s))$

其中， $D sign (s)$ 项是一个附加项，用于说明扰动的上界。定义扰动函数的句柄。

d = @(t) 0.5*sin(t);

更新 SMC 控制器参数。

param.smc.c = 5;
param.smc.k = 3;
param.smc.eta = 0.1;
param.smc.d = 0.6;

为控制输入函数创建一个句柄，并使用 ode45 对系统响应进行仿真。

u = @(x,param) smc(x,param);
[T,Y] = ode45(@(t,x) msdStateDer(t,x,u,param,d),tspan,y0);

计算仿真时间内的滑动面 S 和控制输入值 U。

S = -param.smc.c*Y(:,1) - Y(:,2);
U = smc(Y.',param);

生成绘图以可视化随时间变化的系统响应、相平面、控制输入和滑动面。

plotResponse(T,U,Y,S,"System Response with Disturbances")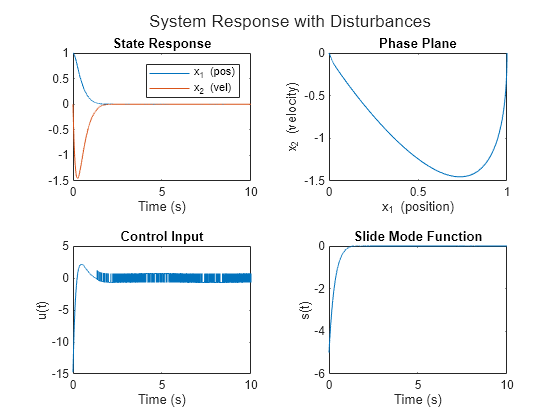

使用准滑动模式控制减少震颤

SMC 中的一个常见问题是震颤，即当系统状态接近滑动面时，控制输入会高频切换。为了减轻震颤，可以采用准滑动模式控制。在这种方法中，控制律中的不连续符号函数会替换为连续近似函数（例如饱和函数）。[3]

对于此示例，使用以下饱和函数。

$sat (s, ϕ) = {\begin{cases} 1 & if s > ϕ \\ s / ϕ & if - ϕ \leq s \leq ϕ \\ - 1 & if s < - ϕ \end{cases}$

其中 $ϕ$ 是边界层厚度。当滑动变量 $s$ 处在边界层 $[\begin{array}{c} - ϕ & ϕ \end{array}]$ 内时，该饱和函数在 $- 1$ 与 $1$ 之间平滑插值，从而减少了高频切换。

使用饱和函数的修改后控制律由下式给出：

$u = \frac{1}{g} (η sat (s, ϕ) + ks + c e_{}^{˙} + {x_{}^{¨}}_{d} - f + D sat (s, ϕ))$

$ϕ$ 的选择至关重要，因为它定义了滑动面周围边界层的厚度。 $ϕ$ 越大，震颤越少，但会增加稳态误差。相反， $ϕ$ 越小，稳态误差也会减小，但会增加震颤。

要实现准滑动模式控制，请使用函数句柄 sat 定义饱和函数，并将边界层厚度 $ϕ$ 设置为 1e-2。

phi = 1e-2;
sat = @(s) min(max(s/phi,-1),1);

更新控制输入函数以包含饱和函数。

u = @(x,param) smc(x,param,sat);

使用更新后的控制律对系统响应进行仿真。

[T,Y] = ode45(@(t,x) msdStateDer(t,x,u,param,d),tspan,y0);

基于仿真时间计算滑动面和控制输入值。

S = -param.smc.c*Y(:,1) - Y(:,2);
U = smc(Y.',param,sat);

使用 QSMC 可视化随时间变化的系统响应、相平面、控制输入和滑动面。

plotResponse(T,U,Y,S,"System Response Using Quasi-Sliding Mode Control")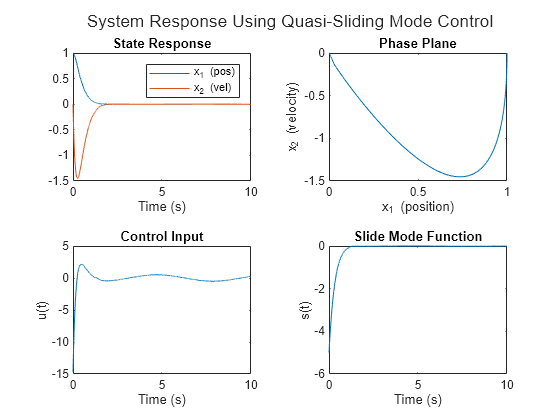

准滑动模式控制系统可实现类似的性能，并且控制输入中没有震颤。

Simulink

在本部分内容中，我们使用 Simulink 中的 Sliding Mode Controller (Reaching Law) 模块设计 SMC 控制器。

打开 Simulink® 模型。

mdl = 'massSpringDamper';
open_system(mdl)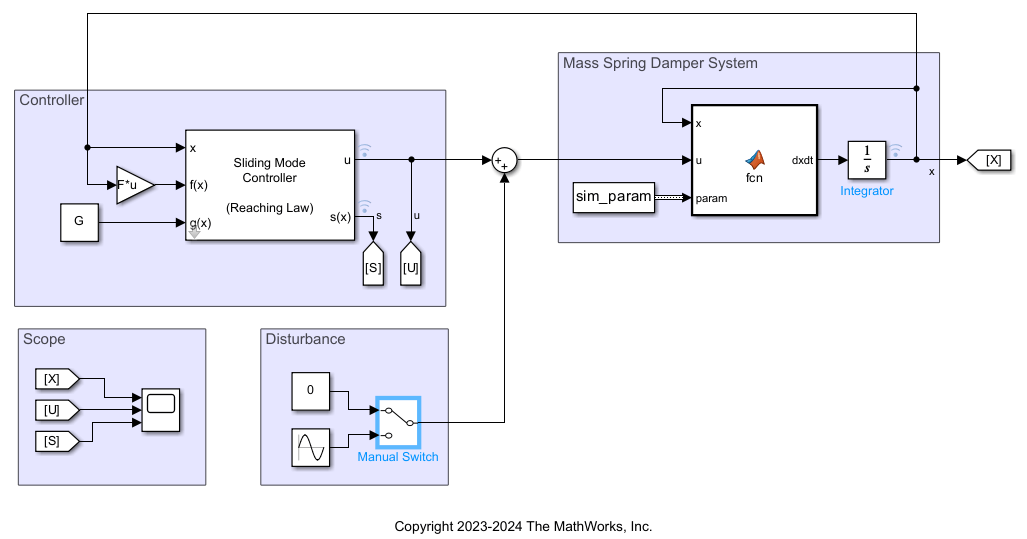

打开 Sliding Mode Controller (Reaching Law) 模块。

open_system(mdl+"/Sliding Mode Controller (Reaching Law)")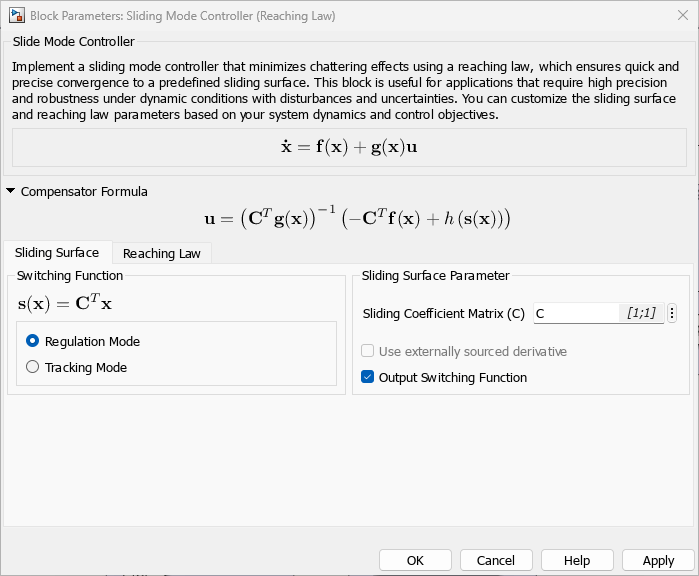

请注意，Sliding Mode Controller (Reaching Law) 以 $\dot{x} = f (x) + g (x) u$ 的形式为动态系统设计一个控制器。

为动态项 $f (x)$ 和 $g (x)$ 定义矩阵 F 和 G。

F = [0 1; -param.Stiffness/param.Mass -param.Damping/param.Mass];
G = [0; 1/param.Mass];

指定滑动系数矩阵。

C = [1;1];

使用“趋近律”选项卡指定所需的趋近律参数：

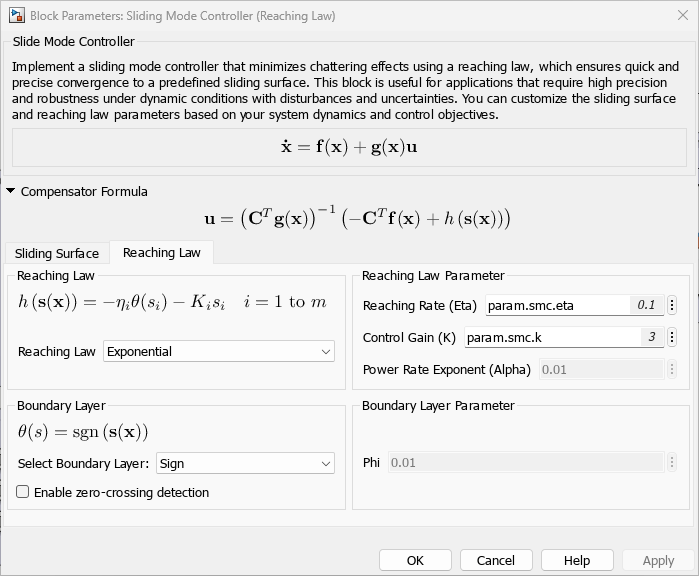
set_param([mdl '/Sliding Mode Controller (Reaching Law)'], 'BoundaryLayer', "Sign");

对于此示例，质量-弹簧-阻尼器参数在 From Workspace 模块中定义。使用 Simulink.Bus.createObject 函数创建总线对象，并相应地更新 From Workspace 输出数据类型。

sim_param = struct( ...
    'Mass', timeseries(param.Mass, 0), ...
    'Damping', timeseries(param.Damping, 0), ...
    'Stiffness', timeseries(param.Stiffness, 0));

busInfo = Simulink.Bus.createObject(param);
set_param([mdl '/From Workspace'], 'OutDataTypeStr', "Bus: " + busInfo.busName);

对模型进行仿真并查看结果。

simout = sim(mdl);

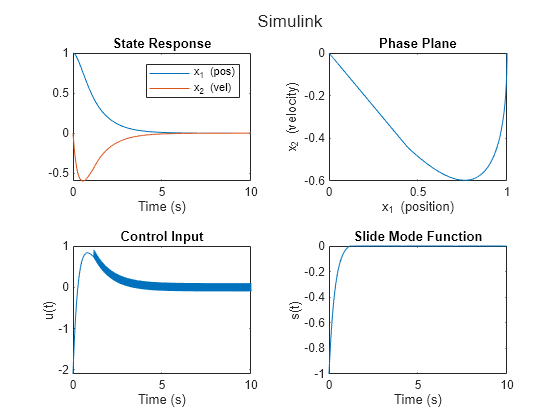
T = simout.logsout.get('x').Values.Time;
U = squeeze(simout.logsout.get('u').Values.Data);
S = squeeze(simout.logsout.get('s').Values.Data);
Y = squeeze(simout.logsout.get('x').Values.Data).';

plotResponse(T,U,Y,S,"Simulink")

参考资料

[1] Derbel, Nabil, Jawhar Ghommam, and Quanmin Zhu, eds.Applications of Sliding Mode Control.Vol. 79.Springer Singapore, 2017.

[2] Weibing Gao, and J.C. Hung.“Variable Structure Control of Nonlinear Systems:A New Approach.”IEEE Transactions on Industrial Electronics 40, no. 1 (February 1993):45–55. https://doi.org/10.1109/41.184820.

[3] Richter, Hanz.Advanced control of turbofan engines.Springer Science & Business Media, 2011.

另请参阅

Sliding Mode Controller (Reaching Law)