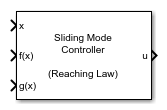
Sliding Mode Controller (Reaching Law)

Design sliding mode controller based on reaching law

Since R2024b

Libraries:
Simulink Control Design / Sliding Mode

Description

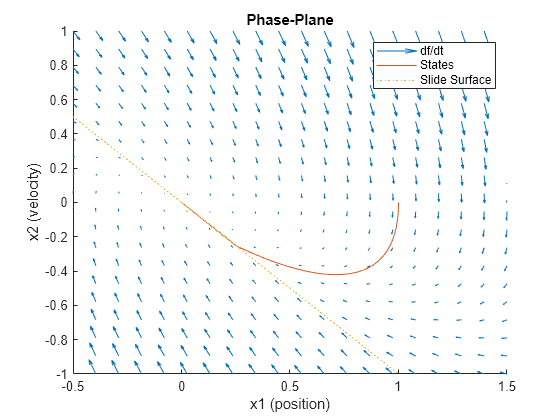
Sliding Mode Control (SMC) is a robust control strategy that brings the system state trajectory to a specified sliding surface and maintains it there. This approach is advantageous for systems requiring high levels of precision and robustness, especially in the presence of disturbances and uncertainties. Once the system reaches the sliding surface, SMC ensures that it stays on this path despite any external or internal changes to system dynamics.

The Sliding Mode Controller block enables you to implement SMC for nonlinear systems characterized by the equation $\dot{x} = f (x) + g (x) u$ . Using this block, you can create a compensator which uses a reaching law, a method that dynamically adjusts control actions to guide the system states toward the sliding surface efficiently. The block provides the following two modes of operation:

Regulation mode
$\begin{array}{l} u = {(C^{T} g (x))}^{- 1} (- C^{T} f (x) + h (s (x))) \\ s (x) = C^{T} x \end{array}$
Tracking mode
$\begin{array}{l} u = {(C^{T} g (x))}^{- 1} (C^{T} {\dot{x}}_{r e f} - C^{T} f (x) + h (s (x))) \\ s (x) = C^{T} (x_{r e f} - x) \end{array}$

Here, C is the sliding coefficient matrix, s(x) is the sliding surface, and h(s(x)) is the reaching law.

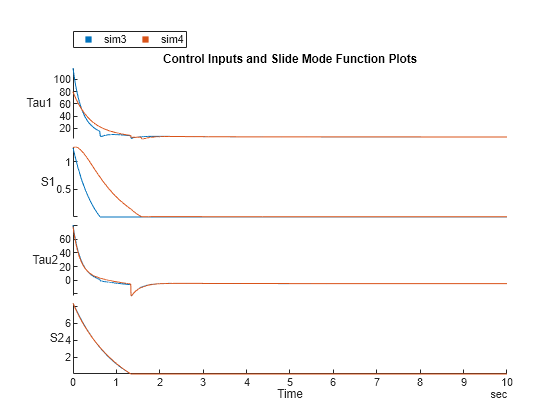
Additionally, SMC minimizes chattering effects, a common challenge in control systems characterized by rapid oscillation or high-frequency switching of the control signal. The block allows you to customize the sliding surface and adjust the reaching law parameters. This enables you to tune the control strategy to your specific system dynamics and objectives, enhancing the system stability and response under varying conditions.

For more information about SMC, see Sliding Mode Control.

Examples

New

Sliding Mode Control Design for Mass-Spring-Damper System

A sliding mode controller defines a sliding surface that the system state converges to and remains on.

Since R2024b
Open Live Script

New

Sliding Mode Control Design for a Robotic Manipulator

Create a sliding mode controller for a robotic manipulator with two actuated joints.

Since R2024b
Open Live Script

Ports

Input

expand all

x — System states
vector

System states, specified as an n_x-by-1 signal, where n_x is the number of states.

Data Types: single | double

f(x) — System dynamics function
vector

System dynamics function f(x) in the systems characterized by the equation $\dot{x} = f (x) + g (x) u$ .

Connect this port to an n_x-by-1 signal, where n_x is the number of states.

Data Types: single | double

g(x) — Input function
vector

Input function g(x) in the systems characterized by the equation $\dot{x} = f (x) + g (x) u$ .

Connect this port to an n_x-by-n_u signal, where n_x is the number of states and n_u is the number of inputs.

Data Types: single | double

x.ref — State reference trajectories
vector

State reference trajectory to follow in the tracking mode, specified as an n_x-by-1 signal, where n_x is the number of states.

Dependencies

To enable this port, set Switching Function to Tracking Mode.

x.ref.dot — Derivative of state reference trajectories
vector

Derivative of state reference trajectory to follow in the tracking mode, specified as an n_x-by-1 signal, where n_x is the number of states.

Use this port when you want to provide the derivative of state reference trajectories from an external input. Otherwise, the block computes the derivative during simulation.

Dependencies

To enable this port:

Set Switching Function to Tracking Mode.
Enable Use externally sourced derivative.

Output

expand all

u — Control action
vector

Computed control action, returned as an n_u-by-1 signal, where n_u is the number of inputs.

s(x) — Sliding variable value
vector

Sliding surface value, returned as an n_u-by-1 signal, where n_u is the number of inputs.

Dependencies

To enable this port, enable the Output Switching Function parameter.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Sliding Surface Tab

Switching Function — Block operation mode
Regulation Mode (default) | Tracking Mode

Block operation mode, specified as one of the following:

Regulation Mode — Use this mode when you want to stabilize the system at a fixed point, that is, bring all the states x to zero.
Tracking Mode — Use this mode when you want the system states to follow a reference trajectory x_ref.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`TaskMode`
Values:	`"Regulation Mode"` (default) \| `"Tracking Mode"`

Example: set_param(gcb,"TaskMode","Tracking Mode")

Sliding Coefficient Matrix (C) — Sliding coefficient matrix
`1` (default) | scalar | column vector | matrix

Sliding coefficient matrix (C), specified as an n_x-by-n_u matrix, where n_x is the number of states and n_u is the number of control inputs.

The matrix C determines the hyperplane to which the sliding mode control drives the system states.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`SlidingMatrix`
Values:	`1` (default) \| scalar in quotes \| column vector in quotes \| matrix in quotes

Example: set_param(gcb,"SlidingMatrix","[1;2]")

Use externally sourced derivative — Specify derivative of state reference externally
`off` (default) | `on`

Select to specify the derivative of state reference signal externally at the input port x.ref.dot.

Dependencies

To enable this parameter, set Switching Function to Tracking Mode.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`EnableTrackingDerivative`
Values:	`"off"` (default) \| `"on"`

Example: set_param(gcb,"EnableTrackingDerivative","on")

Output Switching Function — Output switching function
`off` (default) | `on`

Select to return the sliding surface value at an output port s(x).

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`EnableSwitchingFunction`
Values:	`"off"` (default) \| `"on"`

Example: set_param(gcb,"EnableSwitchingFunction","on")

Reaching Law Tab

Reaching Law — Reaching law
`Constant Rate` (default) | `Exponential` | `Power Rate`

Reaching law h(s(x)) for the sliding surface, specified as one of the following.

Constant Rate — $h (s (x)) = - η_{i} θ (s_{i})$
This law provides a constant rate to reach the sliding surface. Here, θ(s_i) is the boundary layer and η_i is the reaching rate of the ith control input.
Exponential — $h (s (x)) = - η_{i} θ (s_{i}) - K_{i} s_{i}$
This law adds a term proportional to the sliding variable and provides a more aggressive convergence when the state deviation is significant. Here, K_i is the control gain term that scales the control effort associated with the ith sliding variable.
Power Rate — $h {(s (x))}_{i} = - η_{i} {| s_{i} |}^{α} θ (s_{i})$
This law provides fast reaching speed when the state is far away from the sliding surface, but reduces the speed as the state gets near. This ensures reduced chattering and provides fast convergence.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`ReachingLaw`
Values:	`"Constant Rate"` (default) \| `"Exponential"` \| `"Power Rate"`

Example: set_param(gcb,"ReachingLaw","Power Rate")

Reaching Rate (Eta) — Reaching rate
`0.01` (default) | positive scalar | column vector

Reaching rate (η), specified as a positive scalar or a column vector of positive values with length equal to the number of control inputs.

Reaching rate determines the rate at which the system trajectory approaches the sliding surface. A larger value of η results in a faster convergence to the sliding surface but can also lead to higher control effort, which is not desirable in all cases due to potential issues like actuator saturation or increased chattering.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`ReachingRate`
Values:	`"0.01"` (default) \| positive scalar in quotes \| column vector in quotes

Example: set_param(gcb,"ReachingRate","0.05")

Control Gain (K) — Control gain
`0.01` (default) | positive scalar | column vector

Control gain of the proportional term in the exponential reaching law, specified as a positive scalar or column vector of length equal to the number of control inputs. In the exponential reaching law, this term increases the control effort proportional to the deviation from the sliding surface.

Dependencies

To enable this parameter, set Reaching Law to Exponential.

Programmatic Use

To get the block parameter value programmatically, use the get_param function.

Parameter:	`ControlGain`
Values:	`"0.01"` (default) \| positive scalar in quotes \| column vector in quotes

Example: set_param(gcb,"ControlGain","2")

Power Rate Exponent (Alpha) — Power rate exponent
`0.01` (default) | positive scalar between 0 and 1 | column vector of positive values between 0 and 1

Exponent value in the power rate reaching law, specified as a positive scalar between 0 and 1 or column vector of length equal to the number of control inputs. This parameter determines the nonlinearity of the control action with respect to the distance from the sliding surface. Specifically, it adjusts how the control effort scales with the magnitude of the sliding variable. The value of α influences the smoothness of the approach to the sliding surface. The lower values lead to a softer approach and potentially reduce chattering.

Dependencies

To enable this parameter, set Reaching Law to Power Rate.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`PowerRate`
Values:	`"0.01"` (default) \| positive scalar between 0 and 1 in quotes \| column vector of positive values between 0 and 1 in quotes

Example: set_param(gcb,"PowerRate","0.02")

Select Boundary Layer — Boundary layer function
`Sign` (default) | `Relay` | `Hyperbolic Tangent` | `Saturation`

Boundary layer function, specified as one of the following:

Sign — $θ (s) = s g n (s (x))$
This option uses the default signum function and switches between –1 and 1 discontinuously.
Relay — $θ (s) = \frac{s}{| s | + ϕ}$
This option uses a relay function to define the switching boundary around the sliding surface.
Hyperbolic Tangent — $θ (s) = t a n h (\frac{s}{ϕ})$
This option uses a hyperbolic tangent function to define the switching boundary around the sliding surface.
Saturation — $\begin{matrix} θ (s) = {\begin{matrix} \begin{matrix} 1 & s > ϕ \end{matrix} \\ \begin{matrix} k s & s \leq ϕ \end{matrix} \\ \begin{matrix} - 1 & s < - ϕ \end{matrix} \end{matrix} & k = \frac{1}{ϕ} \end{matrix}$
This option uses a saturation function to smoothly interpolate between –1 and 1 when the sliding variable is within the boundary layer [–ϕ,ϕ], which reduces the high-frequency switching.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`BoundaryLayer`
Values:	`"Sign"` (default) \| `"Relay"` \| `"Hyperbolic Tangent"` \| `"Saturation"`

Example: set_param(gcb,""BoundaryLayer,"Saturation")

Enable zero-crossing detection — Enable zero-crossing detection
`off` (default) | `on`

Select to enable zero-crossing detection. For more information, see Zero-Crossing Detection.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`ZeroCross`
Values:	`"off"` (default) \| `"on"`

Example: set_param(gcb,"ZeroCross","on")

Phi — Boundary layer thickness
`0.01` (default) | positive scalar | column vector

Boundary layer thickness parameter, specified as a positive scalar or column vector of length equal to the number of control inputs.

This parameter defines the boundary layer thickness around the sliding surface. A larger Phi value results in less chattering but can increase the steady-state error. Conversely, a smaller Phi value can reduce steady-state error but increase chattering.

Dependencies

To enable this parameter, set Select Boundary Layer to any one of these values:

Relay
Hyperbolic Tangent
Saturation

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`Phi`
Values:	`"0.01"` (default) \| positive scalar in quotes \| column vector in quotes

Example: set_param(gcb,"Phi","0.05")

Version History

Introduced in R2024b

Sliding Mode Controller (Reaching Law)

Description

Examples

Sliding Mode Control Design for Mass-Spring-Damper System

Sliding Mode Control Design for a Robotic Manipulator

Ports

Input

x — System states vector

f(x) — System dynamics function vector

g(x) — Input function vector

x.ref — State reference trajectories vector

Dependencies

x.ref.dot — Derivative of state reference trajectories vector

Dependencies

Output

u — Control action vector

s(x) — Sliding variable value vector

Dependencies

Parameters

Sliding Surface Tab

Switching Function — Block operation mode Regulation Mode (default) | Tracking Mode

Programmatic Use

Sliding Coefficient Matrix (C) — Sliding coefficient matrix 1 (default) | scalar | column vector | matrix

Programmatic Use

Use externally sourced derivative — Specify derivative of state reference externally off (default) | on

Dependencies

Programmatic Use

Output Switching Function — Output switching function off (default) | on

Programmatic Use

Reaching Law Tab

Reaching Law — Reaching law Constant Rate (default) | Exponential | Power Rate

Programmatic Use

Reaching Rate (Eta) — Reaching rate 0.01 (default) | positive scalar | column vector

Programmatic Use

Control Gain (K) — Control gain 0.01 (default) | positive scalar | column vector

Dependencies

Programmatic Use

Power Rate Exponent (Alpha) — Power rate exponent 0.01 (default) | positive scalar between 0 and 1 | column vector of positive values between 0 and 1

Dependencies

Programmatic Use

Select Boundary Layer — Boundary layer function Sign (default) | Relay | Hyperbolic Tangent | Saturation

Programmatic Use

Enable zero-crossing detection — Enable zero-crossing detection off (default) | on

Programmatic Use

Phi — Boundary layer thickness 0.01 (default) | positive scalar | column vector

Dependencies

Programmatic Use

Version History

See Also

Topics

x — System states
vector

f(x) — System dynamics function
vector

g(x) — Input function
vector

x.ref — State reference trajectories
vector

x.ref.dot — Derivative of state reference trajectories
vector

u — Control action
vector

s(x) — Sliding variable value
vector

Switching Function — Block operation mode
Regulation Mode (default) | Tracking Mode

Sliding Coefficient Matrix (C) — Sliding coefficient matrix
`1` (default) | scalar | column vector | matrix

Use externally sourced derivative — Specify derivative of state reference externally
`off` (default) | `on`

Output Switching Function — Output switching function
`off` (default) | `on`

Reaching Law — Reaching law
`Constant Rate` (default) | `Exponential` | `Power Rate`

Reaching Rate (Eta) — Reaching rate
`0.01` (default) | positive scalar | column vector

Control Gain (K) — Control gain
`0.01` (default) | positive scalar | column vector

Power Rate Exponent (Alpha) — Power rate exponent
`0.01` (default) | positive scalar between 0 and 1 | column vector of positive values between 0 and 1

Select Boundary Layer — Boundary layer function
`Sign` (default) | `Relay` | `Hyperbolic Tangent` | `Saturation`

Enable zero-crossing detection — Enable zero-crossing detection
`off` (default) | `on`

Phi — Boundary layer thickness
`0.01` (default) | positive scalar | column vector