Classification Using Nearest Neighbors

Pairwise Distance Metrics

Categorizing query points based on their distance to points in a training data set can be a simple yet effective way of classifying new points. You can use various metrics to determine the distance, described next. Use pdist2 to find the distance between a set of data and query points.

Distance Metrics

Given an mx-by-n data matrix X, which is treated as mx (1-by-n) row vectors x₁, x₂, ..., x_mx, and an my-by-n data matrix Y, which is treated as my (1-by-n) row vectors y₁, y₂, ...,y_my, the various distances between the vector x_s and y_t are defined as follows:

Euclidean distance
$d_{s t}^{2} = (x_{s} - y_{t}) (x_{s} - y_{t})^{'} .$
The Euclidean distance is a special case of the Minkowski distance, where p = 2.
Specify Euclidean distance by setting the Distance parameter to 'euclidean'.
Standardized Euclidean distance
$d_{s t}^{2} = (x_{s} - y_{t}) V^{- 1} (x_{s} - y_{t})^{'},$
where V is the n-by-n diagonal matrix whose jth diagonal element is (S(j))², where S is a vector of scaling factors for each dimension.
Specify standardized Euclidean distance by setting the Distance parameter to 'seuclidean'.
Fast Euclidean distance is the same as Euclidean distance, computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Does not support sparse data. See Fast Euclidean Distance Algorithm.
Specify fast Euclidean distance by setting the Distance parameter to 'fasteuclidean'.
Fast standardized Euclidean distance is the same as standardized Euclidean distance, computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Does not support sparse data. See Fast Euclidean Distance Algorithm.
Specify fast standardized Euclidean distance by setting the Distance parameter to 'fastseuclidean'.
Mahalanobis distance
$d_{s t}^{2} = (x_{s} - y_{t}) C^{- 1} (x_{s} - y_{t})^{'},$
where C is the covariance matrix.
Specify Mahalanobis distance by setting the Distance parameter to 'mahalanobis'.
City block distance
$d_{s t} = \sum_{j = 1}^{n} | x_{s j} - y_{t j} | .$
The city block distance is a special case of the Minkowski distance, where p = 1.
Specify city block distance by setting the Distance parameter to 'cityblock'.
Minkowski distance
$d_{s t} = \sqrt[p]{\sum_{j = 1}^{n} {| x_{s j} - y_{t j} |}^{p}} .$
For the special case of p = 1, the Minkowski distance gives the city block distance. For the special case of p = 2, the Minkowski distance gives the Euclidean distance. For the special case of p = ∞, the Minkowski distance gives the Chebychev distance.
Specify Minkowski distance by setting the Distance parameter to 'minkowski'.
Chebychev distance
$d_{s t} = \max_{j} {| x_{s j} - y_{t j} |} .$
The Chebychev distance is a special case of the Minkowski distance, where p = ∞.
Specify Chebychev distance by setting the Distance parameter to 'chebychev'.
Cosine distance
$d_{s t} = (1 - \frac{x_{s} {y^{'}}_{t}}{\sqrt{(x_{s} {x^{'}}_{s}) (y_{t} {y^{'}}_{t})}}) .$
Specify cosine distance by setting the Distance parameter to 'cosine'.
Correlation distance
$d_{s t} = 1 - \frac{(x_{s} - {\bar{x}}_{s}) {(y_{t} - {\bar{y}}_{t})}^{'}}{\sqrt{(x_{s} - {\bar{x}}_{s}) {(x_{s} - {\bar{x}}_{s})}^{'}} \sqrt{(y_{t} - {\bar{y}}_{t}) {(y_{t} - {\bar{y}}_{t})}^{'}}},$
where
${\bar{x}}_{s} = \frac{1}{n} \sum_{j} x_{s j}$
and
${\bar{y}}_{t} = \frac{1}{n} \sum_{j} y_{t j} .$
Specify correlation distance by setting the Distance parameter to 'correlation'.
Hamming distance is the percentage of coordinates that differ:
$d_{s t} = (# (x_{s j} \neq y_{t j}) / n) .$
Specify Hamming distance by setting the Distance parameter to 'hamming'.
Jaccard distance is one minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ:
$d_{s t} = \frac{# [(x_{s j} \neq y_{t j}) \cap ((x_{s j} \neq 0) \cup (y_{t j} \neq 0))]}{# [(x_{s j} \neq 0) \cup (y_{t j} \neq 0)]} .$
Specify Jaccard distance by setting the Distance parameter to 'jaccard'.
Spearman distance is one minus the sample Spearman's rank correlation between observations (treated as sequences of values):
$d_{s t} = 1 - \frac{(r_{s} - {\bar{r}}_{s}) {(r_{t} - {\bar{r}}_{t})}^{'}}{\sqrt{(r_{s} - {\bar{r}}_{s}) {(r_{s} - {\bar{r}}_{s})}^{'}} \sqrt{(r_{t} - {\bar{r}}_{t}) {(r_{t} - {\bar{r}}_{t})}^{'}}},$
where
- r_sj is the rank of x_sj taken over x_1j, x_2j, ...x_mx,j, as computed by tiedrank.
- r_tj is the rank of y_tj taken over y_1j, y_2j, ...y_my,j, as computed by tiedrank.
- r_s and r_t are the coordinate-wise rank vectors of x_s and y_t, that is, r_s = (r_s₁, r_s₂, ... r_sn) and r_t = (r_t1, r_t2, ... r_tn).
- ${\bar{r}}_{s} = \frac{1}{n} \sum_{j} r_{s j} = \frac{(n + 1)}{2}$ .
- ${\bar{r}}_{t} = \frac{1}{n} \sum_{j} r_{t j} = \frac{(n + 1)}{2}$ .
Specify Spearman distance by setting the Distance parameter to 'spearman'.

k-Nearest Neighbor Search and Radius Search

Given a set X of n points and a distance function, k-nearest neighbor (kNN) search lets you find the k closest points in X to a query point or set of points Y. The kNN search technique and kNN-based algorithms are widely used as benchmark learning rules. The relative simplicity of the kNN search technique makes it easy to compare the results from other classification techniques to kNN results. The technique has been used in various areas such as:

bioinformatics
image processing and data compression
document retrieval
computer vision
multimedia database
marketing data analysis

You can use kNN search for other machine learning algorithms, such as:

kNN classification
local weighted regression
missing data imputation and interpolation
density estimation

You can also use kNN search with many distance-based learning functions, such as K-means clustering.

In contrast, for a positive real value r, rangesearch finds all points in X that are within a distance r of each point in Y. This fixed-radius search is closely related to kNN search, as it supports the same distance metrics and search classes, and uses the same search algorithms.

k-Nearest Neighbor Search Using Exhaustive Search

When your input data meets any of the following criteria, knnsearch uses the exhaustive search method by default to find the k-nearest neighbors:

The number of columns of X is more than 10.
X is sparse.
The distance metric is either:
- 'seuclidean'
- 'mahalanobis'
- 'cosine'
- 'correlation'
- 'spearman'
- 'hamming'
- 'jaccard'
- A custom distance function

knnsearch also uses the exhaustive search method if your search object is an ExhaustiveSearcher model object. The exhaustive search method finds the distance from each query point to every point in X, ranks them in ascending order, and returns the k points with the smallest distances. For example, this diagram shows the k = 3 nearest neighbors.

3-nearest neighbors diagram. knnsearch computes the displayed distances by using the exhaustive search method.

k-Nearest Neighbor Search Using a Kd-Tree

When your input data meets all of the following criteria, knnsearch creates a Kd-tree by default to find the k-nearest neighbors:

The number of columns of X is less than 10.
X is not sparse.
The distance metric is either:
- 'euclidean' (default)
- 'cityblock'
- 'minkowski'
- 'chebychev'

knnsearch also uses a Kd-tree if your search object is a KDTreeSearcher model object.

Kd-trees divide your data into nodes with at most BucketSize (default is 50) points per node, based on coordinates (as opposed to categories). The following diagrams illustrate this concept using patch objects to color code the different “buckets.”

Diagram of data divided into nodes by Kd-tree

When you want to find the k-nearest neighbors to a given query point, knnsearch does the following:

Determines the node to which the query point belongs. In the following example, the query point (32,90) belongs to Node 4.
Finds the closest k points within that node and its distance to the query point. In the following example, the points in red circles are equidistant from the query point, and are the closest points to the query point within Node 4.
Chooses all other nodes having any area that is within the same distance, in any direction, from the query point to the kth closest point. In this example, only Node 3 overlaps the solid black circle centered at the query point with radius equal to the distance to the closest points within Node 4.
Searches nodes within that range for any points closer to the query point. In the following example, the point in a red square is slightly closer to the query point than those within Node 4.

Diagram of nodes and nearest neighbors

Using a Kd-tree for large data sets with fewer than 10 dimensions (columns) can be much more efficient than using the exhaustive search method, as knnsearch needs to calculate only a subset of the distances. To maximize the efficiency of Kd-trees, use a KDTreeSearcher model.

Approximate KNN Search Using Hierarchical Navigable Small Worlds (HNSW) Algorithm

When your data set is large, knnsearch uses a significant amount of time and memory. To perform a more efficient (but approximate) search, use an hnswSearcher model object. You can create the model object by using the hnswSearcher function, or by using the createns function with the specification NSMethod="hnsw". Then use knnsearch with the hnswSearcher model object, which runs faster than the KDTreeSearcher or ExhaustiveSearcher objects, especially when the data has many rows and columns.

Note

Because of the time required to create an hnswSearcher model object, you must create the object before calling knnsearch. That is, you cannot call knnsearch(X,NSMethod="hnsw"). Instead, you must call knnsearch(Mdl,...), where Mdl is an existing hnswSearcher model object.

The HNSW algorithm creates a graph for the nearest neighbor search that consists of a number of layers. The higher layers contain fewer points than the lower layers. Each lower layer contains all the points of the higher layers, plus additional points.

An approximate KNN search starts at the highest layer and greedily finds the closest point in that layer before going to the next lower layer to search. The search stops at Layer 0. The following figure illustrates the search process.

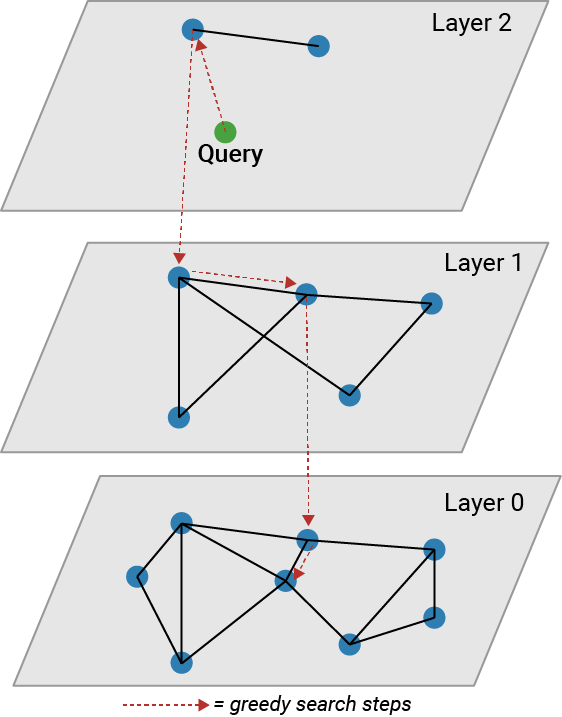
Three layers of an HNSW graph showing an approximate nearest neighbor search

The HNSW algorithm completes the following steps to create an approximate nearest neighbor searcher:

Place a data point in a random layer J, where the level J is drawn from a geometric distribution.
Perform a search for the k-nearest neighbors of the data point in that layer.
Copy the point to layer J – 1.
Find the point's new k-nearest neighbors.
Repeat the process down to layer 0.
Place the next data points, if any, using the same process.

The process of creating an HNSW searcher, which is described in detail in Malkov and Yashunin [1], is relatively slow. The benefit of using an HNSW searcher is increased speed of searching for nearest neighbors of new data points. The KNN search procedure with HNSW might fail to find the true nearest neighbors, because the search might get stuck in a local minimum. However, because the HNSW search process is typically faster than any other type of KNN search, consider using it when you do not need to find all the true nearest neighbors.

The parameter M in Malkov and Yashunin [1] corresponds to the MaxNumLinksPerNode parameter in hnswSearcher. The software sets the parameter M_L in [1] to 1/log(MaxNumLinksPerNode).

What Are Search Model Objects?

Basically, model objects are a convenient way of storing information. Related models have the same properties with values and types relevant to a specified search method. In addition to storing information within models, you can perform certain actions on models.

You can efficiently perform a k-nearest neighbors search on your search model using knnsearch. Or, you can search for all neighbors within a specified radius using your search model and rangesearch. In addition, there are generic knnsearch and rangesearch functions that search without creating or using a model.

To determine which type of model and search method is best for your data, consider the following:

Does your data set have many columns, that is, more than 10? If so, the ExhaustiveSearcher model might perform better. For data with many rows and columns, hnswSearcher runs much faster than other search objects, but returns approximate rather than exact results.
Is your data sparse? Use the ExhaustiveSearcher model.
Do you want to use one of these distance metrics to find the exact nearest neighbors? Use the ExhaustiveSearcher model.
- 'seuclidean'
- 'mahalanobis'
- 'cosine'
- 'correlation'
- 'spearman'
- 'hamming'
- 'jaccard'
- A custom distance function
Is your data set large but contains fewer than 10 columns? Use the KDTreeSearcher model. If your data set is large with many columns, try hnswSearcher.
Are you searching for the nearest neighbors for a large number of query points? Use KDTreeSearcher or hnswSearcher.

Classify Query Data

Open Live Script

This example shows how to classify query data by:

Growing a Kd-tree
Conducting a k nearest neighbor search using the grown tree.
Assigning each query point the class with the highest representation among their respective nearest neighbors.

Classify a new point based on the last two columns of the Fisher iris data. Using only the last two columns makes it easier to plot.

load fisheriris
x = meas(:,3:4);
gscatter(x(:,1),x(:,2),species)
legend('Location','best')

Figure contains an axes object. The axes object contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

Plot the new point.

newpoint = [5 1.45];
line(newpoint(1),newpoint(2),'marker','x','color','k',...
   'markersize',10,'linewidth',2)

Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

Prepare a Kd-tree neighbor searcher model.

Mdl = KDTreeSearcher(x)

Mdl = 
  KDTreeSearcher with properties:

       BucketSize: 50
         Distance: 'euclidean'
    DistParameter: []
                X: [150x2 double]

Mdl is a KDTreeSearcher model. By default, the distance metric it uses to search for neighbors is Euclidean distance.

Find the 10 sample points closest to the new point.

[n,d] = knnsearch(Mdl,newpoint,'k',10);
line(x(n,1),x(n,2),'color',[.5 .5 .5],'marker','o',...
    'linestyle','none','markersize',10)

Figure contains an axes object. The axes object contains 5 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

It appears that knnsearch has found only the nearest eight neighbors. In fact, this particular dataset contains duplicate values.

x(n,:)

ans = 10×2

    5.0000    1.5000
    4.9000    1.5000
    4.9000    1.5000
    5.1000    1.5000
    5.1000    1.6000
    4.8000    1.4000
    5.0000    1.7000
    4.7000    1.4000
    4.7000    1.4000
    4.7000    1.5000

Make the axes equal so the calculated distances correspond to the apparent distances on the plot axis equal and zoom in to see the neighbors better.

xlim([4.5 5.5]);
ylim([1 2]);
axis square

Figure contains an axes object. The axes object contains 5 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

Find the species of the 10 neighbors.

tabulate(species(n))

       Value    Count   Percent
   virginica        2     20.00%
  versicolor        8     80.00%

Using a rule based on the majority vote of the 10 nearest neighbors, you can classify this new point as a versicolor.

Visually identify the neighbors by drawing a circle around the group of them. Define the center and diameter of a circle, based on the location of the new point.

ctr = newpoint - d(end);
diameter = 2*d(end);
% Draw a circle around the 10 nearest neighbors.
h = rectangle('position',[ctr,diameter,diameter],...
   'curvature',[1 1]);
h.LineStyle = ':';

Figure contains an axes object. The axes object contains 6 objects of type line, rectangle. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

Using the same dataset, find the 10 nearest neighbors to three new points.

figure 
newpoint2 = [5 1.45;6 2;2.75 .75];
gscatter(x(:,1),x(:,2),species)
legend('location','best')
[n2,d2] = knnsearch(Mdl,newpoint2,'k',10);
line(x(n2,1),x(n2,2),'color',[.5 .5 .5],'marker','o',...
   'linestyle','none','markersize',10)
line(newpoint2(:,1),newpoint2(:,2),'marker','x','color','k',...
   'markersize',10,'linewidth',2,'linestyle','none')

Figure contains an axes object. The axes object contains 5 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

Find the species of the 10 nearest neighbors for each new point.

tabulate(species(n2(1,:)))

       Value    Count   Percent
   virginica        2     20.00%
  versicolor        8     80.00%

tabulate(species(n2(2,:)))

      Value    Count   Percent
  virginica       10    100.00%

tabulate(species(n2(3,:)))

       Value    Count   Percent
  versicolor        7     70.00%
      setosa        3     30.00%

For more examples using knnsearch methods and function, see the individual reference pages.

Find Nearest Neighbors Using a Custom Distance Metric

Open Live Script

This example shows how to find the indices of the three nearest observations in X to each observation in Y with respect to the chi-square distance. This distance metric is used in correspondence analysis, particularly in ecological applications.

Randomly generate normally distributed data into two matrices. The number of rows can vary, but the number of columns must be equal. This example uses 2-D data for plotting.

rng(1) % For reproducibility
X = randn(50,2);
Y = randn(4,2);

h = zeros(3,1);
figure
h(1) = plot(X(:,1),X(:,2),'bx');
hold on
h(2) = plot(Y(:,1),Y(:,2),'rs','MarkerSize',10);
title('Heterogeneous Data')

Figure contains an axes object. The axes object with title Heterogeneous Data contains 2 objects of type line. One or more of the lines displays its values using only markers

The rows of X and Y correspond to observations, and the columns are, in general, dimensions (for example, predictors).

The chi-square distance between j-dimensional points x and z is

$χ (x, z) = \sqrt{\sum_{j = 1}^{J} w_{j} {(x_{j} - z_{j})}^{2}},$

where $w_{j}$ is the weight associated with dimension j.

Choose weights for each dimension, and specify the chi-square distance function. The distance function must:

Take as input arguments one row of X, e.g., x, and the matrix Z.
Compare x to each row of Z.
Return a vector D of length $n_{z}$ , where $n_{z}$ is the number of rows of Z. Each element of D is the distance between the observation corresponding to x and the observations corresponding to each row of Z.

w = [0.4; 0.6];
chiSqrDist = @(x,Z)sqrt(((x-Z).^2)*w);

This example uses arbitrary weights for illustration.

Find the indices of the three nearest observations in X to each observation in Y.

k = 3;
[Idx,D] = knnsearch(X,Y,'Distance',chiSqrDist,'k',k);

idx and D are 4-by-3 matrices.

idx(j,1) is the row index of the closest observation in X to observation j of Y, and D(j,1) is their distance.
idx(j,2) is the row index of the next closest observation in X to observation j of Y, and D(j,2) is their distance.
And so on.

Identify the nearest observations in the plot.

for j = 1:k
    h(3) = plot(X(Idx(:,j),1),X(Idx(:,j),2),'ko','MarkerSize',10);
end 
legend(h,{'\texttt{X}','\texttt{Y}','Nearest Neighbor'},'Interpreter','latex')
title('Heterogeneous Data and Nearest Neighbors')
hold off

$Figure contains an axes object. The axes object with title Heterogeneous Data and Nearest Neighbors contains 5 objects of type line. One or more of the lines displays its values using only markers These objects represent \texttt{X}, \texttt{Y}, Nearest Neighbor.$

Several observations of Y share nearest neighbors.

Verify that the chi-square distance metric is equivalent to the Euclidean distance metric, but with an optional scaling parameter.

[IdxE,DE] = knnsearch(X,Y,'Distance','seuclidean','k',k, ...
    'Scale',1./(sqrt(w)));
AreDiffIdx = sum(sum(Idx ~= IdxE))

AreDiffIdx = 
0

AreDiffDist = sum(sum(abs(D - DE) > eps))

AreDiffDist = 
0

The indices and distances between the two implementations of three nearest neighbors are practically equivalent.

K-Nearest Neighbor Classification for Supervised Learning

The ClassificationKNN classification model lets you:

Prepare your data for classification according to the procedure in Steps in Supervised Learning. Then, construct the classifier using fitcknn.

Construct KNN Classifier

Open Live Script

This example shows how to construct a k-nearest neighbor classifier for the Fisher iris data.

Load the Fisher iris data.

load fisheriris
X = meas;    % Use all data for fitting
Y = species; % Response data

Construct the classifier using fitcknn.

Mdl = fitcknn(X,Y)

Mdl = 
  ClassificationKNN
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'setosa'  'versicolor'  'virginica'}
           ScoreTransform: 'none'
          NumObservations: 150
                 Distance: 'euclidean'
             NumNeighbors: 1

A default k-nearest neighbor classifier uses a single nearest neighbor only. Often, a classifier is more robust with more neighbors than that.

Change the neighborhood size of Mdl to 4, meaning that Mdl classifies using the four nearest neighbors.

Mdl.NumNeighbors = 4;

Examine Quality of KNN Classifier

Open Live Script

This example shows how to examine the quality of a k-nearest neighbor classifier using resubstitution and cross validation.

Construct a KNN classifier for the Fisher iris data as in Construct KNN Classifier.

load fisheriris
X = meas;    
Y = species; 
rng(10); % For reproducibility
Mdl = fitcknn(X,Y,'NumNeighbors',4);

Examine the resubstitution loss, which, by default, is the fraction of misclassifications from the predictions of Mdl. (For nondefault cost, weights, or priors, see loss.)

rloss = resubLoss(Mdl)

rloss = 
0.0400

The classifier predicts incorrectly for 4% of the training data.

Construct a cross-validated classifier from the model.

CVMdl = crossval(Mdl);

Examine the cross-validation loss, which is the average loss of each cross-validation model when predicting on data that is not used for training.

kloss = kfoldLoss(CVMdl)

kloss = 
0.0333

The cross-validated classification accuracy resembles the resubstitution accuracy. Therefore, you can expect Mdl to misclassify approximately 4% of new data, assuming that the new data has about the same distribution as the training data.

Predict Classification Using KNN Classifier

Open Live Script

This example shows how to predict classification for a k-nearest neighbor classifier.

Construct a KNN classifier for the Fisher iris data as in Construct KNN Classifier.

load fisheriris
X = meas;    
Y = species; 
Mdl = fitcknn(X,Y,'NumNeighbors',4);

Predict the classification of an average flower.

flwr = mean(X); % an average flower
flwrClass = predict(Mdl,flwr)

flwrClass = 1x1 cell array
    {'versicolor'}

Modify KNN Classifier

Open Live Script

This example shows how to modify a k-nearest neighbor classifier.

Construct a KNN classifier for the Fisher iris data as in Construct KNN Classifier.

load fisheriris
X = meas;    
Y = species; 
Mdl = fitcknn(X,Y,'NumNeighbors',4);

Modify the model to use the three nearest neighbors, rather than the default one nearest neighbor.

Mdl.NumNeighbors = 3;

Compare the resubstitution predictions and cross-validation loss with the new number of neighbors.

loss = resubLoss(Mdl)

loss = 
0.0400

rng(10); % For reproducibility
CVMdl = crossval(Mdl,'KFold',5);
kloss = kfoldLoss(CVMdl)

kloss = 
0.0333

In this case, the model with three neighbors has the same cross-validated loss as the model with four neighbors (see Examine Quality of KNN Classifier).

Modify the model to use cosine distance instead of the default, and examine the loss. To use cosine distance, you must recreate the model using the exhaustive search method.

CMdl = fitcknn(X,Y,'NSMethod','exhaustive','Distance','cosine');
CMdl.NumNeighbors = 3;
closs = resubLoss(CMdl)

closs = 
0.0200

The classifier now has lower resubstitution error than before.

Check the quality of a cross-validated version of the new model.

CVCMdl = crossval(CMdl);
kcloss = kfoldLoss(CVCMdl)

kcloss = 
0.0200

CVCMdl has a better cross-validated loss than CVMdl. However, in general, improving the resubstitution error does not necessarily produce a model with better test-sample predictions.

References

[1] Malkov, Yu. A., and D. A. Yashunin. Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs. Available at https://arxiv.org/abs/1603.09320.