detectdrift

Detect drifts between baseline and target data using permutation testing

Since R2022a

Syntax

DDiagnostics = detectdrift(Baseline,Target)

DDiagnostics = detectdrift(Baseline,Target,Name=Value)

Description

DDiagnostics = detectdrift(Baseline,Target) performs Permutation Testing to detect drift for each variable in the Baseline and Target data sets, and returns the results in DDiagnostics.

DDiagnostics is a DriftDiagnostics object.

example

DDiagnostics = detectdrift(Baseline,Target,Name=Value) specifies additional options using one or more of the name-value arguments. For example, you can specify the metrics to use for the variables or the maximum number of permutations.

example

Examples

collapse all

Compare Baseline and Target Data for Potential Drift

Open Live Script

Generate baseline and target data with two variables, where the distribution parameters of the second variable change for the target data.

rng('default') % For reproducibility
baseline = [normrnd(0,1,100,1),wblrnd(1.1,1,100,1)];
target = [normrnd(0,1,100,1),wblrnd(1.2,2,100,1)];

Compare the two data sets for any drift.

DDiagnostics = detectdrift(baseline,target)

DDiagnostics = 
  DriftDiagnostics

              VariableNames: ["x1"    "x2"]
       CategoricalVariables: []
                DriftStatus: ["Stable"    "Drift"]
                    PValues: [0.2850 0.0030]
        ConfidenceIntervals: [2x2 double]
    MultipleTestDriftStatus: "Drift"
             DriftThreshold: 0.0500
           WarningThreshold: 0.1000

DDiagnostics is a DriftDiagnostics object. detectdrift displays some of the object properties.

Display the confidence intervals for the estimated p-values.

DDiagnostics.ConfidenceIntervals

ans = 2×2

    0.2572    0.0006
    0.3141    0.0087

For the first variable, the lower bound of the confidence interval for the estimated p-value is greater than the warning threshold value of 0.1. Therefore, detectdrift determines that the target data for the first variable is stable compared to the baseline data. For the second variable, the upper bound of the confidence interval for the estimated p-value is smaller than the drift threshold of 0.05. Therefore, the drift status for this variable is Drift, which indicates that detectdrift detects the shift in the distribution parameters.

detectdrift uses the default Bonferroni method for testing multiple hypotheses. The function first divides the warning and drift thresholds by the number of p-values, which in this case is two. Then the function determines if any p-value is still lower than either threshold. Here, the second p-value is still lower than the modified drift threshold, so the function sets the MultipleTestDriftStatus to Drift for the overall data.

Visualize the permutation results for both variables.

tiledlayout(2,1);
ax1 = nexttile;
plotPermutationResults(DDiagnostics,ax1,Variable="x1")
ax2 = nexttile;
plotPermutationResults(DDiagnostics,ax2,Variable="x2")

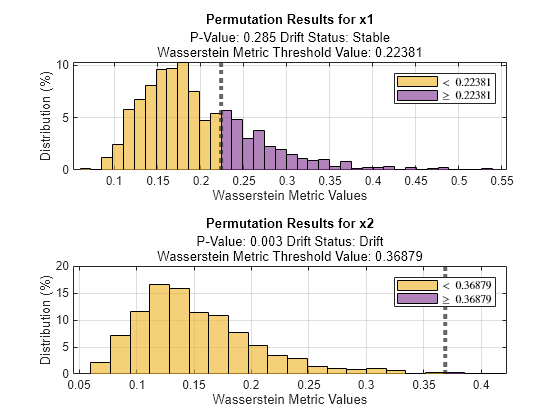
$Figure contains 2 axes objects. Axes object 1 with title Permutation Results for x1, xlabel Wasserstein Metric Values, ylabel Distribution (%) contains 3 objects of type histogram, constantline. These objects represent $<$ 0.22381, $\geq$ 0.22381. Axes object 2 with title Permutation Results for x2, xlabel Wasserstein Metric Values, ylabel Distribution (%) contains 3 objects of type histogram, constantline. These objects represent $<$ 0.36879, $\geq$ 0.36879.$

Bars to the right of the dashed line show the metric values that are greater than the threshold, which is the initial metric value detectdrift computes using the baseline and target data for each variable. The amount of the bars greater than the threshold is much more for variable x1, which indicates that there is not a significant drift between the baseline and target data for this variable.

Specify Options for Data Drift Detection

Open Live Script

Load the sample data.

load humanactivity

For details on the data set, enter Description at the command line.

Assign the first 250 observations as baseline data and next 250 as target data.

baseline = feat(1:250,:);
target = feat(251:500,:);

Test for drift on variables 5 to 10 using a warning threshold of 0.05 and a drift threshold of 0.01. All variables are continuous, so use the Kolmogorov-Smirnov metric for all variables. Specify the False Discovery Rate method as the multiple test correction.

DDiagnostics = detectdrift(baseline(:,5:10),target(:,5:10),WarningThreshold=0.05, ...
        DriftThreshold=0.01,ContinuousMetric="ks",MultipleTestCorrection="fdr")

DDiagnostics = 
  DriftDiagnostics

              VariableNames: ["x1"    "x2"    "x3"    "x4"    "x5"    "x6"]
       CategoricalVariables: []
                DriftStatus: ["Drift"    "Drift"    "Drift"    "Stable"    "Warning"    "Drift"]
                    PValues: [1.0000e-03 1.0000e-03 1.0000e-03 0.8810 0.0110 1.0000e-03]
        ConfidenceIntervals: [2×6 double]
    MultipleTestDriftStatus: "Drift"
             DriftThreshold: 0.0100
           WarningThreshold: 0.0500


  Properties, Methods

Display the confidence intervals for the estimated p-values.

DDiagnostics.ConfidenceIntervals

ans = 2×6

    0.0000    0.0000    0.0000    0.8593    0.0055    0.0000
    0.0056    0.0056    0.0056    0.9004    0.0196    0.0056

The lower confidence bound of the p-value for the 8th variable (variable name x4) is greater than the warning threshold. Therefore, detectdrift determines that the drift status for this variable is "Stable". The upper confidence bound of the p-value for the 9th variable (variable name x5) is greater than the drift threshold, but lower than the warning threshold. Therefore, detectdrift determines that the drift status for this variable is "Warning". Confidence intervals of all other variables are smaller than the drift threshold, so they have a drift status of "Drift". Based on the False Discovery Rate method for multiple test correction, the function determines that the drift status for the overall data is "Drift".

Visualize the p-values with the confidence intervals and corresponding drift status.

plotDriftStatus(DDiagnostics)

The plot shows the estimated p-values with the confidence intervals against the warning and drift thresholds. The estimated p-value for variable x4 and its confidence intervals are higher than the warning threshold. Therefore, the drift status for this variable is "Stable". The upper confidence bound of the p-value for x5 is greater than the drift threshold, but lower than the warning threshold. Therefore, the drift status for this variable is "Warning". Confidence intervals of all other variables are smaller than the drift threshold, so they have a drift status of "Drift".

Specify Variables and Metrics to Use in Data Drift Detection

Open Live Script

Load the data set NYCHousing2015.

load NYCHousing2015

The data set includes 10 variables with information on the sales of properties in New York City in 2015.

Remove outliers and convert the datetime array (SALEDATE) to the month numbers.

idx = isoutlier(NYCHousing2015.SALEPRICE);
NYCHousing2015(idx,:) = [];
NYCHousing2015.SALEDATE = month(NYCHousing2015.SALEDATE);

Define the baseline and target data as information on the sales made in January and July, respectively.

tbl = NYCHousing2015;
baseline = tbl(tbl.SALEDATE==1,:);
target = tbl(tbl.SALEDATE==7,:);

Shuffle the data.

n = numel(baseline(:,1));
rng(1); % For reproducibility
idx = randsample(n,n);
baseline = baseline(idx,:);
n = numel(target(:,1));
idx = randsample(n,n);
target = target(idx,:);

Test for potential drift between the baseline and target data. Specify the categorical variables and the metrics to use with each variable.

DDiagnostics = detectdrift(baseline(1:1500,:),target(1:1500,:), ...
    VariableNames=["BOROUGH","BUILDINGCLASSCATEGORY","LANDSQUAREFEET","GROSSSQUAREFEET","SALEPRICE"], ...
    CategoricalVariables=["BOROUGH","BUILDINGCLASSCATEGORY"], ...
    Metrics=["Hellinger","Hellinger","ad","ks","energy"])

DDiagnostics = 
  DriftDiagnostics

              VariableNames: ["BOROUGH"    "BUILDINGCLASSCATEGORY"    "LANDSQUAREFEET"    "GROSSSQUAREFEET"    "SALEPRICE"]
       CategoricalVariables: [1 2]
                DriftStatus: ["Drift"    "Stable"    "Drift"    "Drift"    "Drift"]
                    PValues: [0.0260 0.1440 0.0070 0.0230 0.0110]
        ConfidenceIntervals: [2×5 double]
    MultipleTestDriftStatus: "Drift"
             DriftThreshold: 0.0500
           WarningThreshold: 0.1000


  Properties, Methods

detectdrift identifies drift between the baseline and target data for all variables except BUILDINGCLASSCATEGORY.

Display the confidence intervals for the estimated p-values.

DDiagnostics.ConfidenceIntervals

ans = 2×5

    0.0171    0.1228    0.0028    0.0146    0.0055
    0.0379    0.1673    0.0144    0.0343    0.0196

Plot a histogram for SALEPRICE.

plotHistogram(DDiagnostics,Variable="SALEPRICE")

The histogram shows the shift in the sale prices for the month of July compared to January.

Plot the empirical cumulative distribution function for the baseline and target data of SALEPRICE.

plotEmpiricalCDF(DDiagnostics,Variable="SALEPRICE")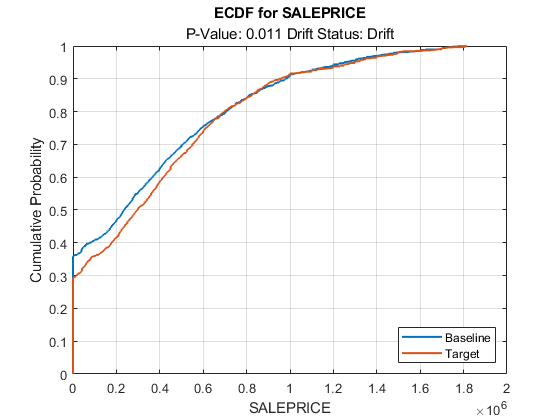

Plot the permutation results for SALEPRICE.

plotPermutationResults(DDiagnostics,Variable="SALEPRICE")

Compute Metrics Without Estimating p-Values

Open Live Script

Generate baseline and target data with three variables, where the distribution parameters of the second and third variables change for the target data.

rng('default') % For reproducibility
baseline = [normrnd(0,1,100,1),wblrnd(1.1,1,100,1),betarnd(1,2,100,1)];
target = [normrnd(0,1,100,1),wblrnd(1.2,2,100,1),betarnd(1.7,2.8,100,1)];

Compute the initial metrics for all variables between the baseline and target data without estimating the p-values.

DDiagnostics = detectdrift(baseline,target,EstimatePValues=false)

DDiagnostics = 
  DriftDiagnostics

           VariableNames: ["x1"    "x2"    "x3"]
    CategoricalVariables: []
                 Metrics: ["Wasserstein"    "Wasserstein"    "Wasserstein"]
            MetricValues: [0.2022 0.3468 0.0559]


  Properties, Methods

detectdrift computes only the initial metric value for each variable using the baseline and target data. The properties associated with permutation testing and p-value estimation are either empty or contain NaNs.

summary(DDiagnostics)

          MetricValue       Metric    
          ___________    _____________

    x1      0.20215      "Wasserstein"
    x2      0.34676      "Wasserstein"
    x3     0.055922      "Wasserstein"

summary function displays only the initial metric value and the metric used for each specified variable.

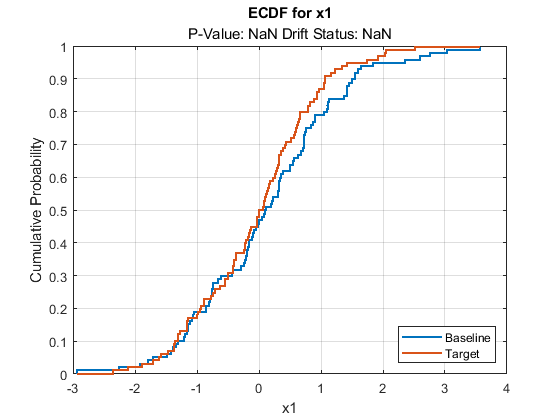
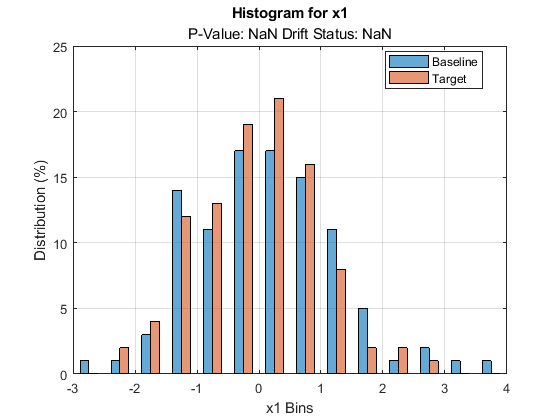
plotDriftStatus and plotPermutationResults do not produce plots and return warning messages when you compute metrics without estimating p-values. plotEmpiricalCDF and plotHistogram plot the ecdf and the histogram, respectively, for the first variable by default. They both return NaN for the p-value and drift status associated with the variable.

plotEmpiricalCDF(DDiagnostics)

plotHistogram(DDiagnostics)

Input Arguments

collapse all

`Baseline` — Baseline data
numeric array | categorical array | table

Baseline data, specified as a numeric array, categorical array, or table. Baseline and Target data must have the same data type. When the input data is a categorical array, detectdrift treats each column as an independent categorical variable.

Data Types: single | double | categorical | table

`Target` — Target data
numeric array | categorical array | table

Target data, specified as a numeric array, categorical array, or table. Baseline and Target data must have the same data type. When the input data is a categorical array, detectdrift treats each column as an independent categorical variable.

Data Types: single | double | categorical | table

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: detectdrift(Baseline,Target,WarningThreshold=0.05,DriftThreshold=0.01,VariableNames=["Weight","MPG"],ContinuousMetrics="ad") sets the warning threshold to 0.05 and drift threshold to 0.01, specifies Weight and MPG as the variables to test for drift detection, and Anderson-Darling as the metric to use in testing all continuous variables.

`VariableNames` — Variables to analyze for drift
string | array of unique strings | character vector | cell array of character vectors

Variables to analyze for drift, specified as a string, array of unique strings, character vector, or cell array of character vectors.

Example: VariableNames=["x1","x3"]

Data Types: string | char | cell

`CategoricalVariables` — List of categorical variables
`"all"` | string | array of unique strings | character vector | cell array of unique character vectors | vector of integer indices | vector of logical indices

List of categorical variables, specified as "all", a string, array of unique strings, character vector, cell array of unique character vectors, vector of integer indices, or vector of logical indices.

detectdrift treats the following as categorical variables: ordinal or nominal data types, or the categorical data type with the ordinal indicator set to true as categorical variables.

Example: CategoricalVariables="Zone"

Data Types: single | double | logical | string | cell

`DriftThreshold` — Threshold for detecting drift
0.05 (default) | scalar value from 0 to 1

Threshold for detecting drift, specified as a scalar value from 0 to 1.

detectdrift uses the drift threshold together with warning threshold to determine the drift status. The DriftThreshold value must be strictly lower than WarningThreshold value.

If the confidence interval for an estimated p-value is (Lower,Upper), then detectdrift determines the drift status as follows.

Drift Status	Condition
Drift	Upper < `DriftThreshold`
Warning	`DriftThreshold` < Lower < `WarningThreshold` or `DriftThreshold` < Upper < `WarningThreshold`
Stable	Lower > `WarningThreshold`

Example: DriftThreshold=0.01

Data Types: single | double

`WarningThreshold` — Threshold for potential drift warning
0.1 (default) | scalar value between 0 and 1

Threshold for potential drift warning, specified as a scalar value between 0 and 1.

detectdrift uses the warning threshold together with drift threshold to determine the drift status. The WarningThreshold value must be strictly greater than the DriftThreshold value.

If the confidence interval for an estimated p-value is (Lower,Upper), then detectdrift determines the drift status as follows.

Drift Status	Condition
Drift	Upper < `DriftThreshold`
Warning	`DriftThreshold` < Lower < `WarningThreshold` or `DriftThreshold` < Upper < `WarningThreshold`
Stable	Lower > `WarningThreshold`

Example: WarningThreshold=0.05

Data Types: single | double

`MaxNumPermutations` — Maximum number of permutations
1000 (default) | positive integer value

Maximum number of permutations, specified as a positive integer value. detectdrift increases the number of trials for permutation logarithmically, according to a heuristic algorithm, until it determines the drift status or reaches MaxNumPermutations. If detectdrift cannot determine the drift status by the end of the maximum number of permutations, then it sets the drift status to "Warning".

Example: MaxNumPermutations=1500

Data Types: single | double

`Metrics` — Metrics used to detect drift for each variable
string | string vector | character vector | cell array of character vectors | function handle | cell array of function handles | structure

Metrics used to detect drift for each variable, specified as one of the following:

String, string vector, character vector, or cell array of character vectors representing one or more of the built-in metrics.
Built-in metrics for continuous variables
Value Definition
"wasserstein" Wasserstein
"energy" Energy
"ks" Kolmogorov-Smirnov
"ad" Anderson-Darling
Built-in metrics for categorical variables
Value Definition
"tv" Total Variation
"psi" Population Stability Index
"hellinger" Hellinger
"chi2" Chi-Square
"bhattacharyya" Bhattacharyya
Function handle or a cell array of function handles. If you provide a function handle FUN as a metric, detectdrift calls it as:
FUN(BaselineVariable,TargetVariable),
where BaselineVariable is the variable in Baseline and TargetVariable is the variable in Target. The output of FUN must be a scalar representing the metric value.
Structure or a cell array of structures, where each structure contains a single field whose value is a function handle. If you pass a structure, detectdrift uses the field name as the metric name. If the function handle is anonymous, detectdrift names it 'CustomMetric_i', where i is the position of the variable in Metrics.

Value	Definition
`"wasserstein"`	Wasserstein
`"energy"`	Energy
`"ks"`	Kolmogorov-Smirnov
`"ad"`	Anderson-Darling

Value	Definition
`"tv"`	Total Variation
`"psi"`	Population Stability Index
`"hellinger"`	Hellinger
`"chi2"`	Chi-Square
`"bhattacharyya"`	Bhattacharyya

Metrics must contain one value for each variable in VariableNames and its size must be equal to the size of VariableNames.

If you specify metrics using Metrics, you cannot specify them using ContinuousMetric or CategoricalMetric.

Example: Metrics=["wasserstein","psi","hellinger"]

Data Types: string | cell | function_handle | struct

`ContinuousMetric` — Metric for drift detection in continuous variables
`"wasserstein"` (default) | string | character vector | function handle | structure

Metric for drift detection in continuous variables, specified as one of the following:

String or a character vector representing one or more of the built-in metrics.
Built-in metrics for continuous variables
Value Definition
"wasserstein" Wasserstein
"energy" Energy
"ks" Kolmogorov-Smirnov
"ad" Anderson-Darling
Function handle called as:
FUN(BaselineVariable,TargetVariable),
where BaselineVariable is the variable in Baseline and TargetVariable is the variable in Target. The output of FUN must be a scalar representing the metric value.
If the function handle is not anonymous, detectdrift extracts the metric name from the provided function handle. If the function handle is anonymous, then it names the metric 'CustomContinuousMetric'.
Structure with a single field whose value is a function handle. In this case, detectdrift uses the field name as the metric name.

Value	Definition
`"wasserstein"`	Wasserstein
`"energy"`	Energy
`"ks"`	Kolmogorov-Smirnov
`"ad"`	Anderson-Darling

If you specify ContinuousMetric, then you cannot specify other metrics using Metrics.

Example: ContinuousMetric="ks"

Data Types: string | char | function_handle | struct

`CategoricalMetric` — Metric for drift detection in categorical variables
`"hellinger"` (default) | string | character vector | function handle | structure

Metric for drift detection in categorical variables, specified as one of the following:

String or a character vector representing one or more of the built-in metrics.
Built-in metrics for categorical variables
Value Definition
"tv" Total Variation
"psi" Population Stability Index
"hellinger" Hellinger
"chi2" Chi-Square
"bhattacharyya" Bhattacharyya
Function handle called as follows:
FUN(BaselineVariable,TargetVariable),
where BaselineVariable is the variable in Baseline and TargetVariable is the variable in Target. The output of FUN must be a scalar representing the metric value.
If the function handle is not anonymous, detectdrift extracts the metric name from the provided function handle. If the function handle is anonymous, then it names the metric 'CustomCategoricalMetric'.
Structure with a single field whose value is a function handle. In this case, detectdrift uses the field name as the metric name.

Value	Definition
`"tv"`	Total Variation
`"psi"`	Population Stability Index
`"hellinger"`	Hellinger
`"chi2"`	Chi-Square
`"bhattacharyya"`	Bhattacharyya

If you specify CategoricalMetric, then you cannot specify other metrics using Metrics.

Example: CategoricalMetric="chi2"

Data Types: string | char | function_handle | struct

`MultipleTestCorrection` — Correction method for multiple hypothesis tests
`"bonferroni"` (default) | `"fdr"`

Correction method for multiple hypothesis tests, specified as one of the following.

"bonferroni" – Bonferroni correction. If k variables are specified for drift detection, detectdrift modifies the warning threshold and drift threshold by dividing each by k. Then, the function checks if any p-values are smaller than the modified threshold values to determine the drift status.
"fdr" – False discovery rate (FDR) method. detectdrift uses the Benjamini-Hochberg procedure to compute the false discovery rate. If k variables are specified for drift detection, the FDR method takes these steps:
1. Rank the p-values corresponding to the specified variables.
2. Divide the ranks 1 to k by the number of variables k to obtain Q = [1/k, 2/k, 3/k ,…, k/k].
3. Modify the warning and drift thresholds for each sorted p-value by multiplying the initial warning and drift threshold values by the corresponding q value. For example, the modified warning threshold for rank 3 is (WarningThreshold)*3/k.
4. Check if any sorted p-values are smaller than the corresponding modified warning or drift thresholds to determine the drift status.

The multiple test correction methods provide a conservative estimate of the multivariable drift.

Example: MultipleTestCorrection="fdr"

`Options` — Options for computing in parallel and setting random streams
structure

Options for computing in parallel and setting random streams, specified as a structure. Create the Options structure using statset. This table lists the option fields and their values.

Field Name Value Default

UseParallel Set this value to true to run computations in parallel. false

Field Name	Value	Default
`UseParallel`	Set this value to `true` to run computations in parallel.	`false`
`UseSubstreams`	Set this value to `true` to run computations in a reproducible manner. To compute reproducibly, set `Streams` to a type that allows substreams: `"mlfg6331_64"` or `"mrg32k3a"`.	`false`
`Streams`	Specify this value as a `RandStream` object or cell array of such objects. Use a single object except when the `UseParallel` value is `true` and the `UseSubstreams` value is `false`. In that case, use a cell array that has the same size as the parallel pool.	If you do not specify `Streams`, then `detectdrift` uses the default stream or streams.

UseSubstreams

Set this value to true to run computations in a reproducible manner.

To compute reproducibly, set Streams to a type that allows substreams: "mlfg6331_64" or "mrg32k3a".

false

Streams Specify this value as a RandStream object or cell array of such objects. Use a single object except when the UseParallel value is true and the UseSubstreams value is false. In that case, use a cell array that has the same size as the parallel pool. If you do not specify Streams, then detectdrift uses the default stream or streams.

Note

You need Parallel Computing Toolbox™ to run computations in parallel.

Example: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))

Data Types: struct

`EstimatePValues` — Indicator to estimate p-values
`true` (default) | `false`

Indicator to estimate the p-values during permutation testing, specified as true or false. If you specify EstimatePValues=false, then detectdrift computes the metrics only.

Example: EstimatePValues=false

Output Arguments

collapse all

`DDiagnostics` — Results of permutation testing for drift detection
`DriftDiagnostics` object

Results of permutation testing for drift detection, returned as a DriftDiagnostics object. detectdrift displays the following properties.

Property Name	Description
`VariableNames`	Variables analyzed for drift detection
`CategoricalVariables`	Indices of categorical variables in the data
`DriftStatus`	Drift status for each variable
`PValues`	Estimated p-value for each variable
`ConfidenceIntervals`	95% confidence interval bounds for the estimated p-values
`MultipleTestDriftStatus`	Drift status for the overall data
`DriftThreshold`	Threshold to determine the drift status
`WarningThreshold`	Threshold to determine the warning status

For a full list of the properties and their descriptions, see the DriftDiagnostics reference page.

Algorithms

collapse all

Permutation Testing

detectdrift uses permutation testing [1] to determine the drift status for each variable in the Baseline data and its counterpart in the Target data. A permutation test is a nonparametric statistical significance test in which the function obtains distribution of a metric (test statistic) under the null hypothesis by computing the values of that metric under all possible rearrangements of a variable in Baseline and Target. Depending on the number of variables and observations, trying all possible permutations of a variable might be infeasible. Therefore detectdrift performs a sufficient number of permutations to obtain a good estimate of the metric for the variable.

Under null hypothesis (no drift), many values of the metric recorded during permutation testing can be as extreme as the initial test statistic. This suggests sufficiently high confidence that the observations of the specified variable in the baseline and target data come from the same distribution. Therefore, no evidence of drift is found, and detectdrift fails to reject the null hypothesis.

If the initial test statistic is identified as an outlier, then detectdrift rejects the null hypothesis. This suggest sufficiently high confidence that the observations of the specified variable in the baseline and target data come from different distributions. Therefore, drift is detected.

detectdrift takes these steps in permutation testing:

For a given variable with m observations in the baseline data and n observations in the target data, detectdrift computes an initial value of the metric from the original data.
The function then permutes the observations of the variable in the baseline and target data and separates them into two vectors with sizes m and n, respectively. Next, the function computes the same metric value. detectdrift repeats this step for MaxNumPermutations times to obtain a distribution of the specified metric.
An estimate of the p-value is p = x/perm, where x is the number of times a metric value obtained from a permutation is greater than the value of the initial metric value, and perm is the number of permutations. With the binomial distribution assumption for x, detectdrift estimates the 95% confidence interval for the p-value by using [~,CI] = binofit(x,perm,0.05).

Given the confidence intervals (Lower, Upper) of the p-values, detectdrift determines the drift status based on the following conditions.

Drift Status	Condition
Drift	Upper < `DriftThreshold`
Warning	`DriftThreshold` < Lower < `WarningThreshold` or `DriftThreshold` < Upper < `WarningThreshold`
Stable	Lower > `WarningThreshold`

Metrics

detectdrift uses the following metrics as test statistics in permutation testing for detecting drift between the baseline and target data.

Metrics for Continuous Variables

The detectdrift function first defines the following:

$E_{b} (x)$ as the empirical cumulative distribution function (ecdf) of the baseline data over the common domain
$E_{t} (x)$ as the ecdf of the target data over the common domain
$D (x)$ as the joint ecdf of all data, and w as the difference between the edges of the bins

Next, detectdrift computes the metrics for continuous variables as follows:

Wasserstein
$W = \sum_{x} w * | E_{b} (x) - E_{t} (x) |$
Energy
$E n = \sqrt{2 * \sum_{x} w * {| E_{b} (x) - E_{t} (x) |}^{2}}$
Kolmogorov-Smirnov
$K S = \max | E_{b} (x) - E_{t} (x) |$
Anderson-Darling
$A D = {\sum_{x} (\frac{| E_{b} (x) - E_{t} (x) |}{\sqrt{(m + n) D (x) * (1 - D (x))}})}^{2}$
m and n are the number of observations in the baseline data and target data, respectively.

Metrics for Categorical Variables

The detectdrift function defines the following:

$H_{b} (x)$ as the percentage of the baseline data in the bins determined by combining the baseline and target data (jointly considering them across the same domain)
$H_{t} (x)$ as the percentage of the target data in the bins determined by combining the baseline and target data

Next, detectdrift computes the metrics for categorical variables as follows:

Total Variation
$T V = 0.5 * \sum_{x} | H_{b} (x) - H_{t} (x) |$
Population Stability Index
$P S I = \max (0, \sum_{x} \log (\frac{H_{t} (x)}{H_{b} (x)}) (H_{t} (x) - H_{b} (x)))$
Chi-Square
$χ^{2} = \sum_{x} \frac{{(H_{t} (x) - H_{b} (x))}^{2}}{H_{b} (x)}$
Bhattacharyya
$B = \max (0, - \log (\min (1, \sum_{x} \sqrt{H_{b} (x) * H_{t} (x)})))$
Hellinger
$H = \max (0, \sqrt{1 - (\min (1, \sum_{x} \sqrt{H_{b} (x) * H_{t} (x)}))})$

To handle empty bins (categories), detectdrift adds a 0.5 correction factor to histogram bin counts for each bin. This is equivalent to the assumption that the parameter p, which is the probability that the value of the variable is in that category, has the prior distribution Beta(0.5,0.5) (Jeffreys prior assumption for the distribution parameter).

References

[1] Hesterbeg,Tim, David S. Moore, Shaun Monaghan, Ashley Clipson, and Rachel Epstein. "Bootstrap Methods and Permutation Tests" in Introduction to the Practice of Statistics. 7th ed, W.H. Freeman, pp. 1–57, 2010.

[2] Benjamini, Yoav, and Yosef Hochberg. "Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing." Journal of the Royal Statistical Society, Series B (Methodological). Vol. 57, No. 1, pp. 289-300, 1995.

[3] Villani, Cédric. Topics in Optimal Transportation. Graduate Studies in Mathematics. Vol. 58, American Mathematical Society, 2000.

[4] Deza, Elena, and Michel Marie Deza. Encyclopedia of Distances, Springer Berlin Heidelberg, 2009.

Extended Capabilities

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To run in parallel, specify the Options name-value argument in the call to this function and set the UseParallel field of the options structure to true using statset:

Options=statset(UseParallel=true)

For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).

Version History

Introduced in R2022a

detectdrift

Syntax

Description

Examples

Compare Baseline and Target Data for Potential Drift

Specify Options for Data Drift Detection

Specify Variables and Metrics to Use in Data Drift Detection

Compute Metrics Without Estimating p-Values

Input Arguments

Baseline — Baseline data numeric array | categorical array | table

Target — Target data numeric array | categorical array | table

Name-Value Arguments

VariableNames — Variables to analyze for drift string | array of unique strings | character vector | cell array of character vectors

CategoricalVariables — List of categorical variables "all" | string | array of unique strings | character vector | cell array of unique character vectors | vector of integer indices | vector of logical indices

DriftThreshold — Threshold for detecting drift 0.05 (default) | scalar value from 0 to 1

WarningThreshold — Threshold for potential drift warning 0.1 (default) | scalar value between 0 and 1

MaxNumPermutations — Maximum number of permutations 1000 (default) | positive integer value

Metrics — Metrics used to detect drift for each variable string | string vector | character vector | cell array of character vectors | function handle | cell array of function handles | structure

ContinuousMetric — Metric for drift detection in continuous variables "wasserstein" (default) | string | character vector | function handle | structure

CategoricalMetric — Metric for drift detection in categorical variables "hellinger" (default) | string | character vector | function handle | structure

MultipleTestCorrection — Correction method for multiple hypothesis tests "bonferroni" (default) | "fdr"

Options — Options for computing in parallel and setting random streams structure

EstimatePValues — Indicator to estimate p-values true (default) | false

Output Arguments

DDiagnostics — Results of permutation testing for drift detection DriftDiagnostics object

Algorithms

Permutation Testing

Metrics

References

Extended Capabilities

Automatic Parallel Support Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

Version History

See Also

`Baseline` — Baseline data
numeric array | categorical array | table

`Target` — Target data
numeric array | categorical array | table

`VariableNames` — Variables to analyze for drift
string | array of unique strings | character vector | cell array of character vectors

`CategoricalVariables` — List of categorical variables
`"all"` | string | array of unique strings | character vector | cell array of unique character vectors | vector of integer indices | vector of logical indices

`DriftThreshold` — Threshold for detecting drift
0.05 (default) | scalar value from 0 to 1

`WarningThreshold` — Threshold for potential drift warning
0.1 (default) | scalar value between 0 and 1

`MaxNumPermutations` — Maximum number of permutations
1000 (default) | positive integer value

`Metrics` — Metrics used to detect drift for each variable
string | string vector | character vector | cell array of character vectors | function handle | cell array of function handles | structure

`ContinuousMetric` — Metric for drift detection in continuous variables
`"wasserstein"` (default) | string | character vector | function handle | structure

`CategoricalMetric` — Metric for drift detection in categorical variables
`"hellinger"` (default) | string | character vector | function handle | structure

`MultipleTestCorrection` — Correction method for multiple hypothesis tests
`"bonferroni"` (default) | `"fdr"`

`Options` — Options for computing in parallel and setting random streams
structure

`EstimatePValues` — Indicator to estimate p-values
`true` (default) | `false`

`DDiagnostics` — Results of permutation testing for drift detection
`DriftDiagnostics` object

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.