hist3
(Not recommended) Bivariate histogram plot
hist3 is not recommended. Use histogram2 instead.
Syntax
Description
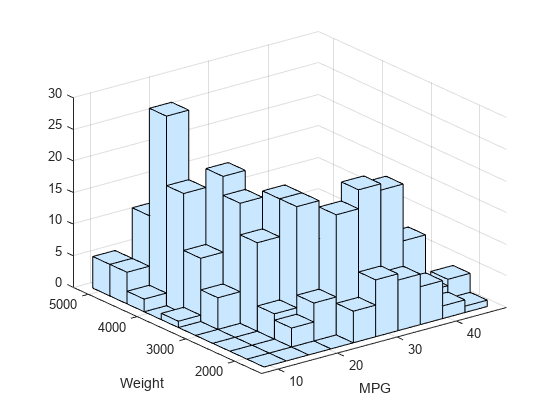
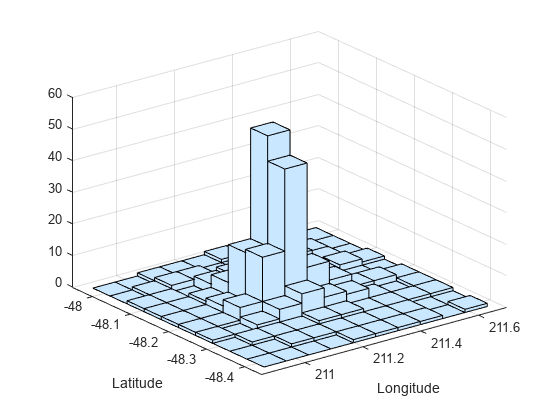
hist3( creates a bivariate
histogram plot of X)X(:,1) and X(:,2) using
10-by-10 equally spaced bins. The hist3 function displays
the bins as 3-D rectangular bars, and the height of each bar indicates the
number of elements in the bin.
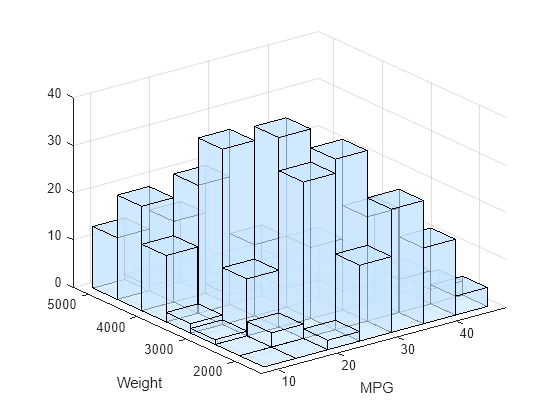
hist3(___,
specifies graphical properties using one or more name-value pair arguments in
addition to the input arguments in the previous syntaxes. For example,
Name,Value)'FaceAlpha',0.5 creates a semitransparent histogram. For
a list of properties, see Surface Properties.
hist3( plots into
the axes specified by ax,___)ax instead of the current axes
(gca). The option ax can precede any
of the input argument combinations in the previous syntaxes.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
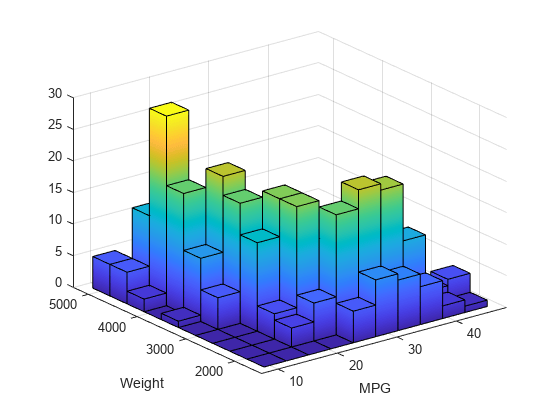
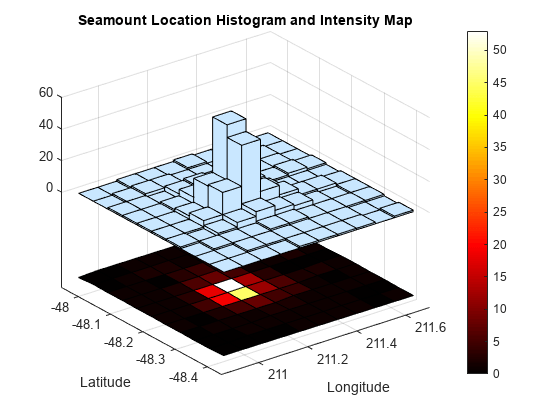
The hist3 function creates a bivariate histogram, which is a type
of surface plot. You can specify surface properties using one or more name-value pair
arguments. Also, you can change the appearance of the histogram by changing the surface
property values after you create a histogram. Get the handle of the surface object by
using s = findobj(gca,'Type','Surface'), and then use
s to modify the surface properties. For an example, see Adjust Graphical Properties. For a list of properties, see Surface Properties.
Alternative Functionality
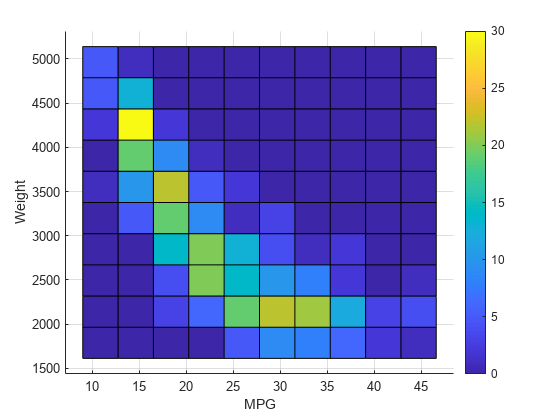
The histogram2 function enables you to create a
bivariate histogram using a Histogram2 object. You can use the
name-value pair arguments of histogram2 to use normalization (Normalization),
adjust the width of the bins in each dimension (BinWidth), and display
the histogram as a rectangular array of tiles instead of 3-D bars (DisplayStyle).
Version History
Introduced before R2006a
See Also
accumarray | bar3 | histcounts2 | histogram2 | binScatterPlot