kstest
单样本柯尔莫哥洛夫-斯米尔诺夫检验
说明
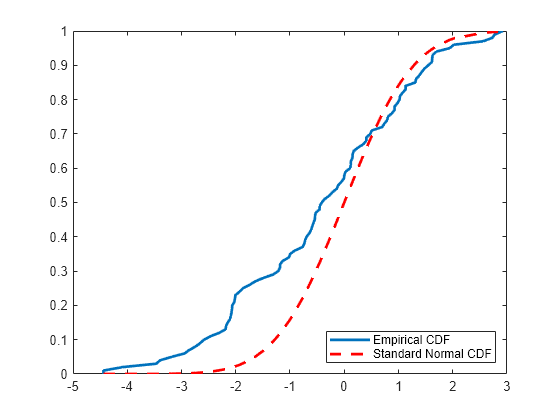
h = kstest(x)x 中的数据来自标准正态分布,而不支持来自非标准正态分布这一备择假设。如果检验在 5% 的显著性水平上拒绝原假设,则结果 h 为 1,否则为 0。
h = kstest(x,Name,Value)
示例
输入参数
名称-值参数
输出参量
详细信息
算法
kstest 通过比较 p 值 p 与显著性水平 Alpha(而不是通过比较检验统计量 ksstat 与临界值 cv)决定拒绝原假设。由于 cv 是逼近值,因此将 ksstat 与 cv 进行比较,得出的结论有时不同于将 p 与 Alpha 进行比较得出的结论。
参考
[1] Massey, F. J. “The Kolmogorov-Smirnov Test for Goodness of Fit.” Journal of the American Statistical Association. Vol. 46, No. 253, 1951, pp. 68–78.
[2] Miller, L. H. “Table of Percentage Points of Kolmogorov Statistics.” Journal of the American Statistical Association. Vol. 51, No. 273, 1956, pp. 111–121.
[3] Marsaglia, G., W. Tsang, and J. Wang. “Evaluating Kolmogorov’s Distribution.” Journal of Statistical Software. Vol. 8, Issue 18, 2003.
版本历史记录
在 R2006a 之前推出
另请参阅
kstest2 | lillietest | adtest