Main Content

Test Ensemble Quality

Open Live Script

You cannot evaluate the predictive quality of an ensemble based on its performance on training data. Ensembles tend to "overtrain," meaning they produce overly optimistic estimates of their predictive power. This means the result of resubLoss for classification (resubLoss for regression) usually indicates lower error than you get on new data.

To obtain a better idea of the quality of an ensemble, use one of these methods:

  • Evaluate the ensemble on an independent test set (useful when you have a lot of training data).

  • Evaluate the ensemble by cross validation (useful when you don't have a lot of training data).

  • Evaluate the ensemble on out-of-bag data (useful when you create a bagged ensemble with fitcensemble or fitrensemble).

This example uses a bagged ensemble so it can use all three methods of evaluating ensemble quality.

Generate an artificial dataset with 20 predictors. Each entry is a random number from 0 to 1. The initial classification is Y=1 if X1+X2+X3+X4+X5>2.5 and Y=0 otherwise.

rng(1,'twister') % For reproducibility
X = rand(2000,20);
Y = sum(X(:,1:5),2) > 2.5;

In addition, to add noise to the results, randomly switch 10% of the classifications.

idx = randsample(2000,200);
Y(idx) = ~Y(idx);

Independent Test Set

Create independent training and test sets of data. Use 70% of the data for a training set by calling cvpartition using the holdout option.

cvpart = cvpartition(Y,'holdout',0.3);
Xtrain = X(training(cvpart),:);
Ytrain = Y(training(cvpart),:);
Xtest = X(test(cvpart),:);
Ytest = Y(test(cvpart),:);

Create a bagged classification ensemble of 200 trees from the training data.

t = templateTree('Reproducible',true);  % For reproducibility of random predictor selections
bag = fitcensemble(Xtrain,Ytrain,'Method','Bag','NumLearningCycles',200,'Learners',t)
bag = 
  ClassificationBaggedEnsemble
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: [0 1]
           ScoreTransform: 'none'
          NumObservations: 1400
               NumTrained: 200
                   Method: 'Bag'
             LearnerNames: {'Tree'}
     ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
                  FitInfo: []
       FitInfoDescription: 'None'
                FResample: 1
                  Replace: 1
         UseObsForLearner: [1400x200 logical]

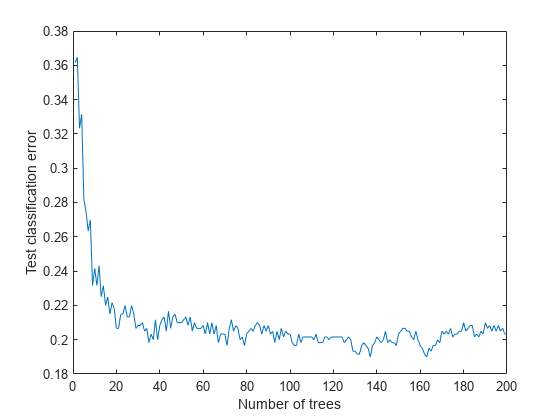
Plot the loss (misclassification) of the test data as a function of the number of trained trees in the ensemble.

figure
plot(loss(bag,Xtest,Ytest,'mode','cumulative'))
xlabel('Number of trees')
ylabel('Test classification error')

Figure contains an axes object. The axes object with xlabel Number of trees, ylabel Test classification error contains an object of type line.

Cross Validation

Generate a five-fold cross-validated bagged ensemble.

cv = fitcensemble(X,Y,'Method','Bag','NumLearningCycles',200,'Kfold',5,'Learners',t)
cv = 
  ClassificationPartitionedEnsemble
    CrossValidatedModel: 'Bag'
         PredictorNames: {'x1'  'x2'  'x3'  'x4'  'x5'  'x6'  'x7'  'x8'  'x9'  'x10'  'x11'  'x12'  'x13'  'x14'  'x15'  'x16'  'x17'  'x18'  'x19'  'x20'}
           ResponseName: 'Y'
        NumObservations: 2000
                  KFold: 5
              Partition: [1x1 cvpartition]
      NumTrainedPerFold: [200 200 200 200 200]
             ClassNames: [0 1]
         ScoreTransform: 'none'

Examine the cross-validation loss as a function of the number of trees in the ensemble.

figure
plot(loss(bag,Xtest,Ytest,'mode','cumulative'))
hold on
plot(kfoldLoss(cv,'mode','cumulative'),'r.')
hold off
xlabel('Number of trees')
ylabel('Classification error')
legend('Test','Cross-validation','Location','NE')

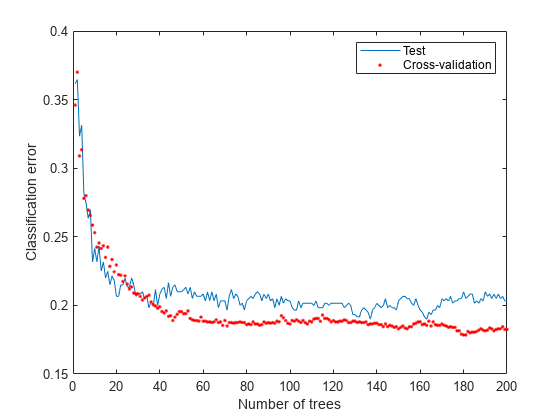
Figure contains an axes object. The axes object with xlabel Number of trees, ylabel Classification error contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Test, Cross-validation.

Cross validating gives comparable estimates to those of the independent set.

Out-of-Bag Estimates

Generate the loss curve for out-of-bag estimates, and plot it along with the other curves.

figure
plot(loss(bag,Xtest,Ytest,'mode','cumulative'))
hold on
plot(kfoldLoss(cv,'mode','cumulative'),'r.')
plot(oobLoss(bag,'mode','cumulative'),'k--')
hold off
xlabel('Number of trees')
ylabel('Classification error')
legend('Test','Cross-validation','Out of bag','Location','NE')

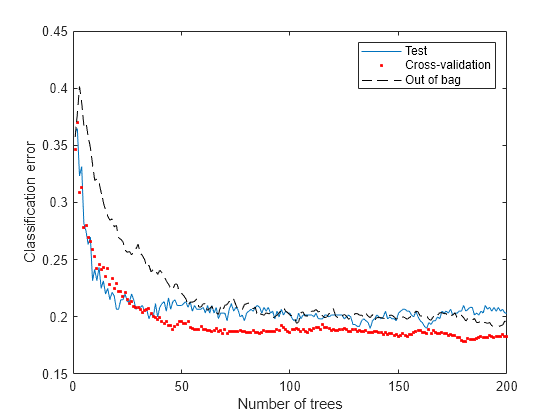
Figure contains an axes object. The axes object with xlabel Number of trees, ylabel Classification error contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Test, Cross-validation, Out of bag.

The out-of-bag estimates are again comparable to those of the other methods.

See Also

| | | | | | |

Related Topics