wblplot
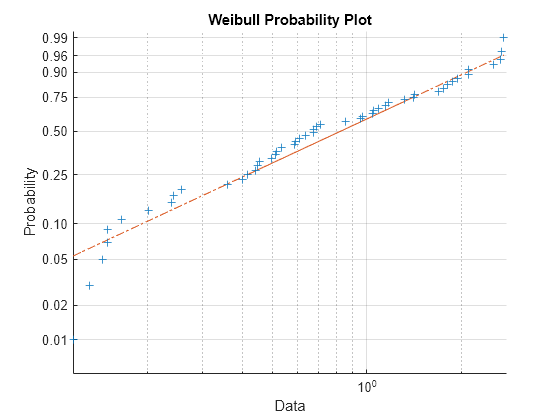
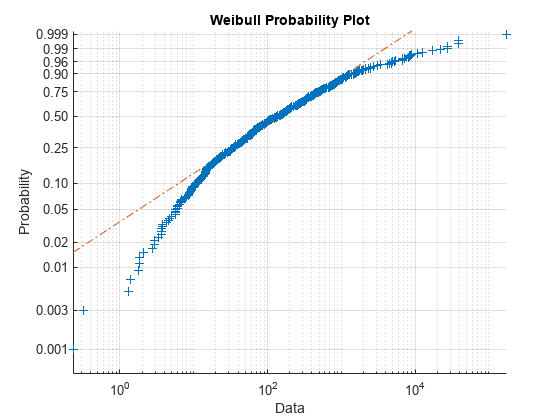
Weibull probability plot
Description
wblplot( creates a Weibull probability
plot comparing the distribution of the data in x)x to the Weibull
distribution.
wblplot plots each data point in x
using plus sign ('+') markers and draws two reference lines that
represent the theoretical distribution. A solid reference line connects the first
and third quartiles of the data, and a dashed reference line extends the solid line
to the ends of the data. If the sample data has a Weibull distribution, then the
data points appear along the reference line. A distribution other than Weibull
introduces curvature in the data plot.
h = wblplot(___)
Examples
Input Arguments
Output Arguments
Algorithms
wblplot matches the quantiles of sample data to the quantiles of
a Weibull distribution. The sample data is sorted, scaled logarithmically, and plotted
on the x-axis. The y-axis represents the quantiles of the Weibull distribution,
converted into probability values. Therefore, the y-axis scaling is not linear.
Where the x-axis value is the ith sorted value from a sample of size N, the y-axis value is the midpoint between evaluation points of the empirical cumulative distribution function of the data. The midpoint is equal to .
wblplot superimposes a reference line to assess the linearity of
the plot. The line goes through the first and third quartiles of the data.
Alternative Functionality
You can use the probplot function to create a probability
plot. The probplot function enables you to indicate censored data
and specify the distribution for a probability plot.
Version History
Introduced before R2006a