Introduction to Wavelet Families

Several families of wavelets that have proven to be especially useful are included in this toolbox. What follows is an introduction to some wavelet families.

You can visualize the wavelets included in this toolbox.

To visualize the analytic Morse, Morlet, and bump wavelets in time and frequency, use cwtfilterbank.
To visualize orthogonal and biorthogonal wavelets in time and frequency, use dwtfilterbank.
To visualize in time other wavelets such as the Meyer, Morlet, Gaussian, Mexican hat, and Shannon wavelets, use wavefun.
To display wavelet packets, use wpfun.
To obtain more information on a wavelet family, use waveinfo.

Haar

Any discussion of wavelets begins with Haar wavelet, the first and simplest. The Haar wavelet is discontinuous, and resembles a step function. It represents the same wavelet as Daubechies db1.

Daubechies

Ingrid Daubechies, one of the brightest stars in the world of wavelet research, invented what are called compactly supported orthonormal wavelets — thus making discrete wavelet analysis practicable.

The names of the Daubechies family wavelets are written dbN, where N is the order, and db the “surname” of the wavelet. The db1 wavelet, as mentioned above, is the same as Haar wavelet. Here are the wavelet functions psi of the next nine members of the family:

You can obtain a survey of the main properties of this family by typing waveinfo('db') from the MATLAB^® command line. See Daubechies Wavelets: dbN in the Wavelet Toolbox User's Guide for more detail.

Biorthogonal

This family of wavelets exhibits the property of linear phase, which is needed for signal and image reconstruction. By using two wavelets, one for decomposition (on the left side) and the other for reconstruction (on the right side) instead of the same single one, interesting properties are derived.

You can obtain a survey of the main properties of this family by typing waveinfo('bior') from the MATLAB command line. See Biorthogonal Wavelet Pairs: biorNr.Nd in the Wavelet Toolbox User's Guide for more detail.

Coiflets

Built by I. Daubechies at the request of R. Coifman. The wavelet function has 2N moments equal to 0 and the scaling function has 2N-1 moments equal to 0. The two functions have a support of length 6N-1. You can obtain a survey of the main properties of this family by typing waveinfo('coif') from the MATLAB command line. See Coiflet Wavelets: coifN in the Wavelet Toolbox User's Guide for more detail.

Symlets

The symlets are nearly symmetrical wavelets proposed by Daubechies as modifications to the db family. The properties of the two wavelet families are similar. Here are the wavelet functions psi.

You can obtain a survey of the main properties of this family by typing waveinfo('sym') from the MATLAB command line. See Symlet Wavelets: symN in the Wavelet Toolbox User's Guide for more detail.

Morlet

This wavelet has no scaling function, but is explicit.

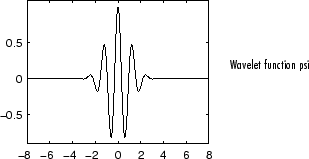
You can obtain a survey of the main properties of this family by typing waveinfo('morl') from the MATLAB command line. See Morlet Wavelet: morl in the Wavelet Toolbox User's Guide for more detail.

Mexican Hat

This wavelet has no scaling function and is derived from a function that is proportional to the second derivative function of the Gaussian probability density function. It is also knows as the Ricker wavelet.

You can obtain a survey of the main properties of this family by typing waveinfo('mexh') from the MATLAB command line. See Mexican Hat Wavelet: mexh in the Wavelet Toolbox User's Guide for more information.

Meyer

The Meyer wavelet and scaling function are defined in the frequency domain.

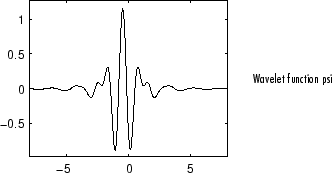
You can obtain a survey of the main properties of this family by typing waveinfo('meyer') from the MATLAB command line. See Meyer Wavelet: meyr in the Wavelet Toolbox User's Guide for more detail.

Other Real Wavelets

Some other real wavelets are available in the toolbox:

Reverse Biorthogonal
Gaussian derivatives family
FIR based approximation of the Meyer wavelet

See Additional Real Wavelets in the Wavelet Toolbox User's Guide for more information.

Complex Wavelets

Some complex wavelet families are available in the toolbox:

Gaussian derivatives
Morlet
Frequency B-Spline
Shannon

See Complex Wavelets in the Wavelet Toolbox User's Guide for more information.